LeetCode 第 78 题:“子集”题解
题解地址:回溯 + 位掩码(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:78. 子集。
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
回溯 + 位掩码(Python 代码、Java 代码)
思路分析:
这道题告诉我们整数数组 nums 不包含重复元素。因此作图,画出递归树结构是关键。
- 因为是组合问题,所以我们按顺序读字符,就不需要设置
used数组; - 经过分析,我们知道,在根结点、非叶子结点和叶子结点都需要结算,因此
res.apppend(path[:])就要放在“中间”位置。
方法一:回溯
回溯的过程是执行一次深度优先遍历,一条路走到底,走不通的时候,返回回来,继续执行,一直这样下去,直到回到起点。
![]()
参考代码 1:在回溯的过程中记录结点。
Python 代码:
from typing import List
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
size = len(nums)
if size == 0:
return []
res = []
self.__dfs(nums, 0, [], res)
return res
def __dfs(self, nums, start, path, res):
res.append(path[:])
for i in range(start, len(nums)):
path.append(nums[i])
# 因为 nums 不包含重复元素,并且每一个元素只能使用一次
# 所以下一次搜索从 i + 1 开始
self.__dfs(nums, i + 1, path, res)
path.pop()
Java 代码:
import java.util.ArrayList;
import java.util.List;
// 给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
// 说明:解集不能包含重复的子集。
// 输入: nums = [1,2,3]
// 输出:[[3],[1],[2],[1,2,3],[1,3],[2,3],[1,2],[]]
public class Solution {
private List<List<Integer>> res;
private void find(int[] nums, int begin, List<Integer> pre) {
// 没有显式的递归终止
res.add(new ArrayList<>(pre));// 注意:Java 的引用传递机制,这里要 new 一下
for (int i = begin; i < nums.length; i++) {
pre.add(nums[i]);
find(nums, i + 1, pre);
pre.remove(pre.size() - 1);// 组合问题,状态在递归完成后要重置
}
}
public List<List<Integer>> subsets(int[] nums) {
int len = nums.length;
res = new ArrayList<>();
if (len == 0) {
return res;
}
List<Integer> pre = new ArrayList<>();
find(nums, 0, pre);
return res;
}
}
参考代码 2:在回溯的过程中记录深度。
Python 代码:
from typing import List
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
size = len(nums)
if size == 0:
return []
res = []
for i in range(size + 1):
self.__dfs(nums, i, 0, [], res)
return res
def __dfs(self, nums, depth, begin, path, res):
# 深度等于 path 长度的时候递归终止
if len(path) == depth:
res.append(path[:])
return
# 按顺序来的,所以不用设置 used 数组
for i in range(begin, len(nums)):
path.append(nums[i])
print(path)
self.__dfs(nums, depth, i + 1, path, res)
path.pop()
Java 代码:
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class Solution {
public List<List<Integer>> subsets(int[] nums) {
int size = nums.length;
List<List<Integer>> res = new ArrayList<>();
if (size == 0) {
return res;
}
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < size + 1; i++) {
dfs(nums, 0, i, stack, res);
}
return res;
}
private void dfs(int[] nums, int start, int depth, Stack<Integer> path, List<List<Integer>> res) {
if (depth == path.size()) {
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i < nums.length; i++) {
path.add(nums[i]);
dfs(nums, i + 1, depth, path, res);
path.pop();
}
}
public static void main(String[] args) {
int[] nums = {1, 2, 3};
Solution solution = new Solution();
List<List<Integer>> subsets = solution.subsets(nums);
System.out.println(subsets);
}
}
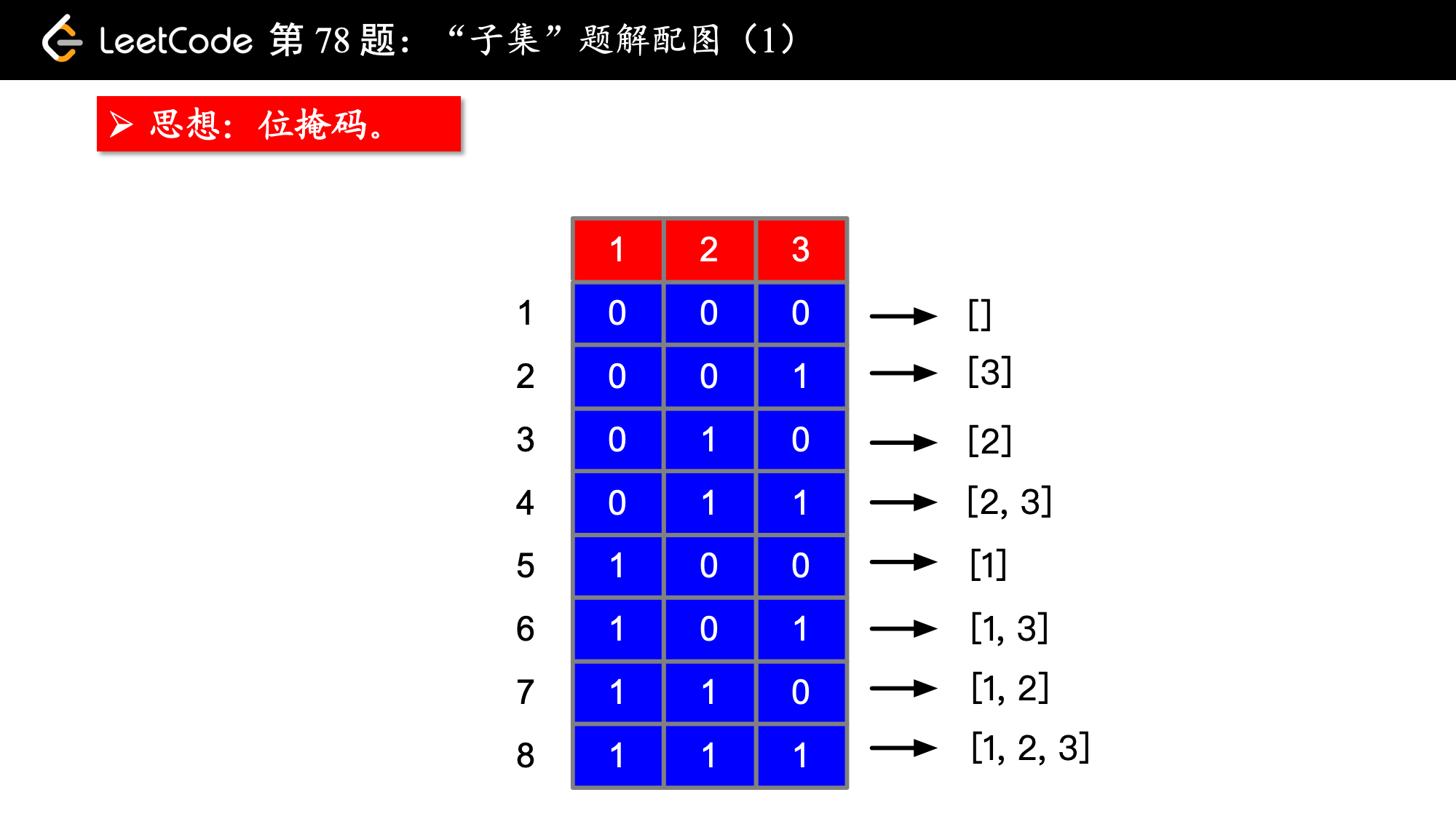
方法二:使用位掩码
数组的每个元素,可以有两个状态:
1、不在子数组中(用 表示);
2、在子数组中(用 表示)。
从 0 到 2 的数组个数次幂(不包括)的整数的二进制表示就能表示所有状态的组合。
参考代码:
Python 代码:
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
size = len(nums)
n = 1 << size
res = []
for i in range(n):
cur = []
for j in range(size):
if i >> j & 1:
cur.append(nums[j])
res.append(cur)
return res
Java 代码:
import java.util.ArrayList;
import java.util.List;
public class Solution5 {
public List<List<Integer>> subsets(int[] nums) {
int size = nums.length;
int n = 1 << size;
List<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < n; i++) {
List<Integer> cur = new ArrayList<>();
for (int j = 0; j < size; j++) {
if (((i >> j) & 1) == 1) {
cur.add(nums[j]);
}
}
res.add(cur);
}
return res;
}
public static void main(String[] args) {
int[] nums = {1, 2, 3};
Solution5 solution5 = new Solution5();
List<List<Integer>> subsets = solution5.subsets(nums);
System.out.println(subsets);
}
}