LeetCode 第 47 题:“全排列 II”题解
题解地址:回溯 + 剪枝(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:47. 全排列 II。
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1,1,2] 输出: [ [1,1,2], [1,2,1], [2,1,1] ]
回溯 + 剪枝(Python 代码、Java 代码)
思路分析:
这一题是在 「力扣」第 46 题:全排列 的基础上增加了“序列中的元素可重复”这一条件。因此使用的方法还是“回溯算法”,只不过在构建递归树的过程中需要剪枝。
在第 46 题中,如果没有重复元素画出的树形图是这样的。
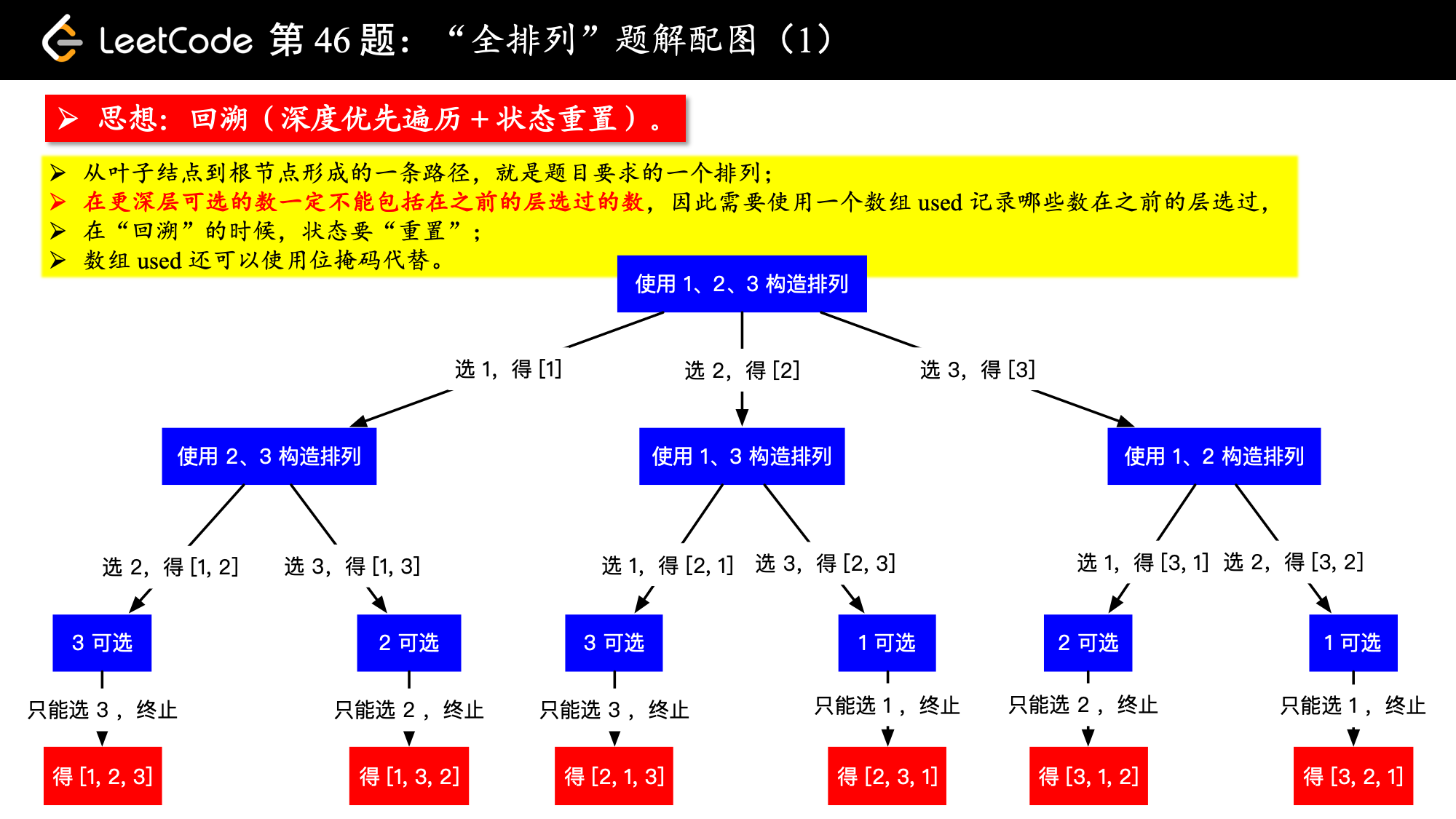
我下面的描述基于我写的 「力扣」第 46 题:全排列的题解 《回溯算法(Python 代码、Java 代码) 。
方法:回溯 + 剪枝
下面这段话是解决有重复元素的序列的排列问题的关键:
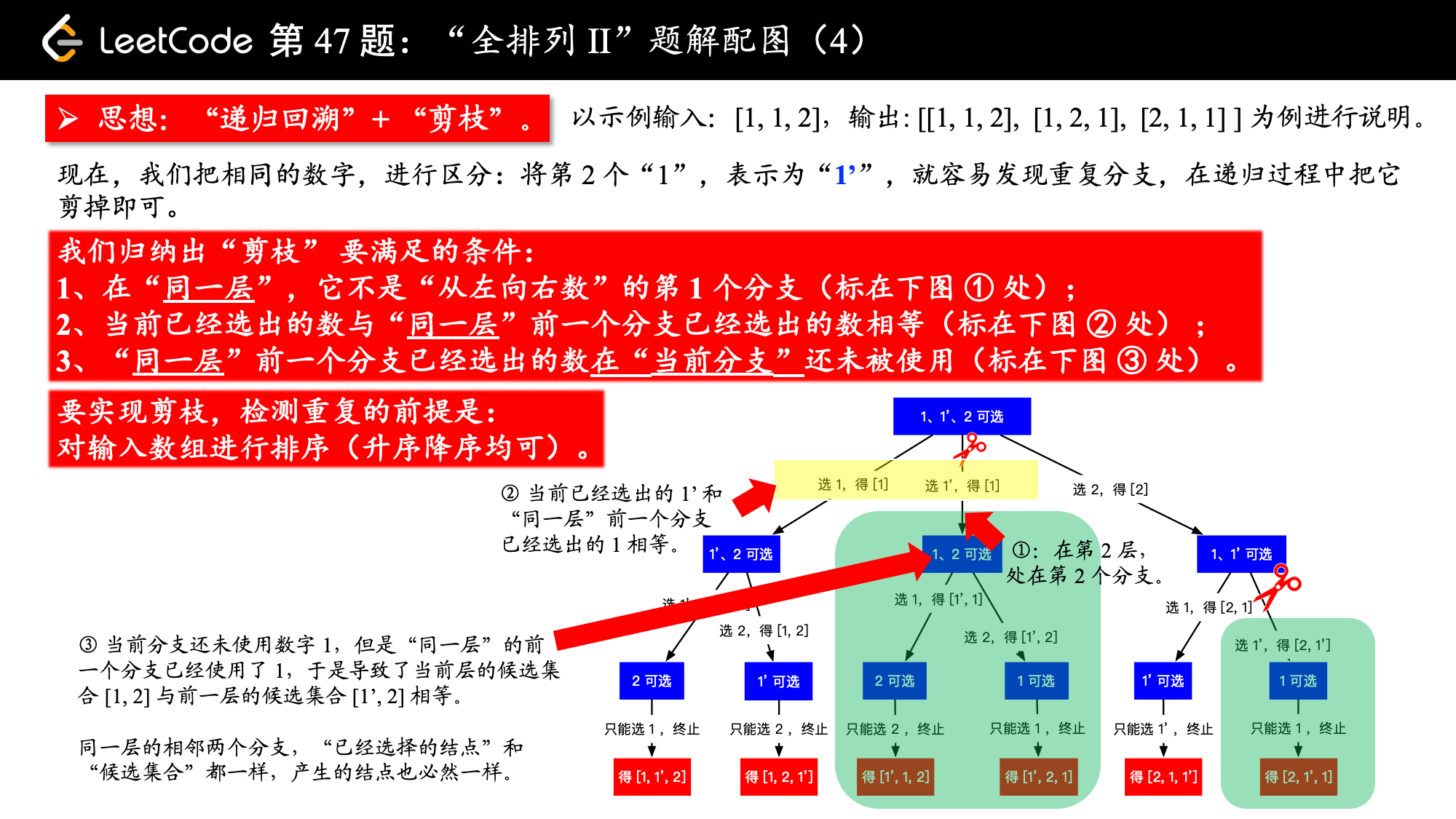
当数组中,有了重复元素的时候,其实也不难,我们可以先把数组排个序,这样在递归的过程中就可以很容易发现重复的元素。当发现重复元素的时候,让这一个分支跳过,就达到了“剪枝”的效果,重复的排列就不会出现在结果集中。
请看下图,我们把排序以后的数组,就当做它没有重复元素的话,还按照之前的回溯方法,也很容易看出重复的分支,把它剪去即可。
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
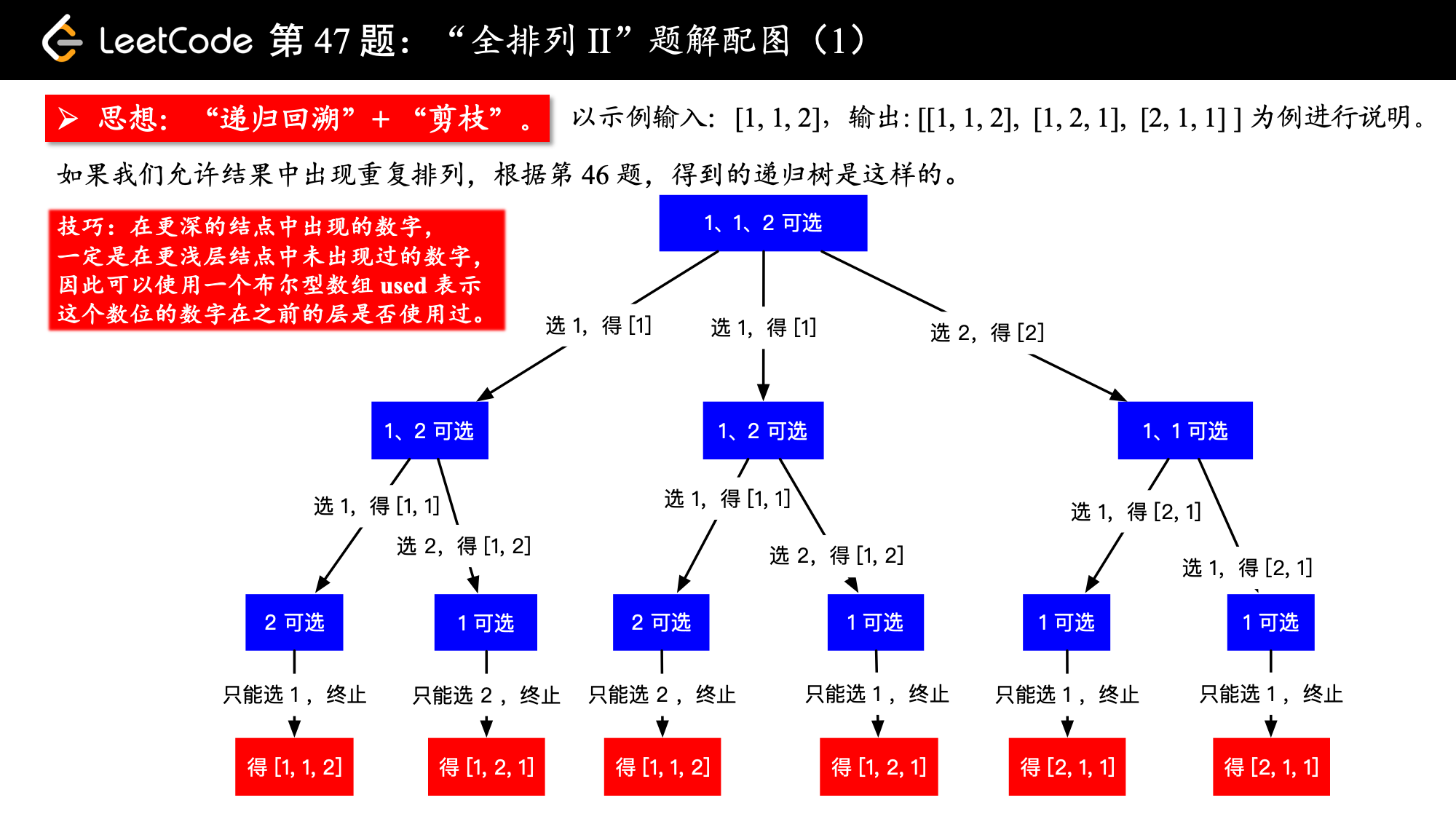
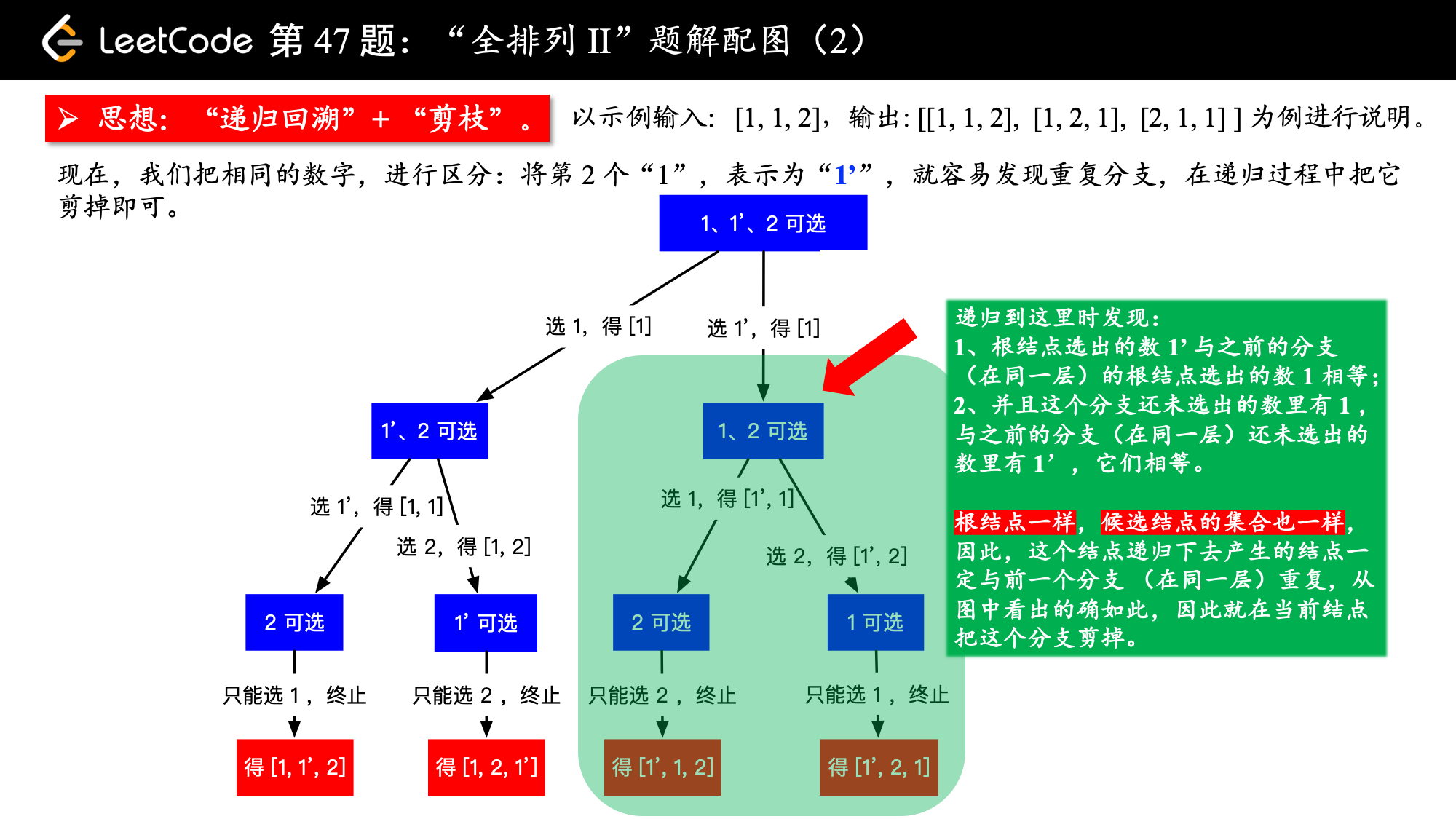
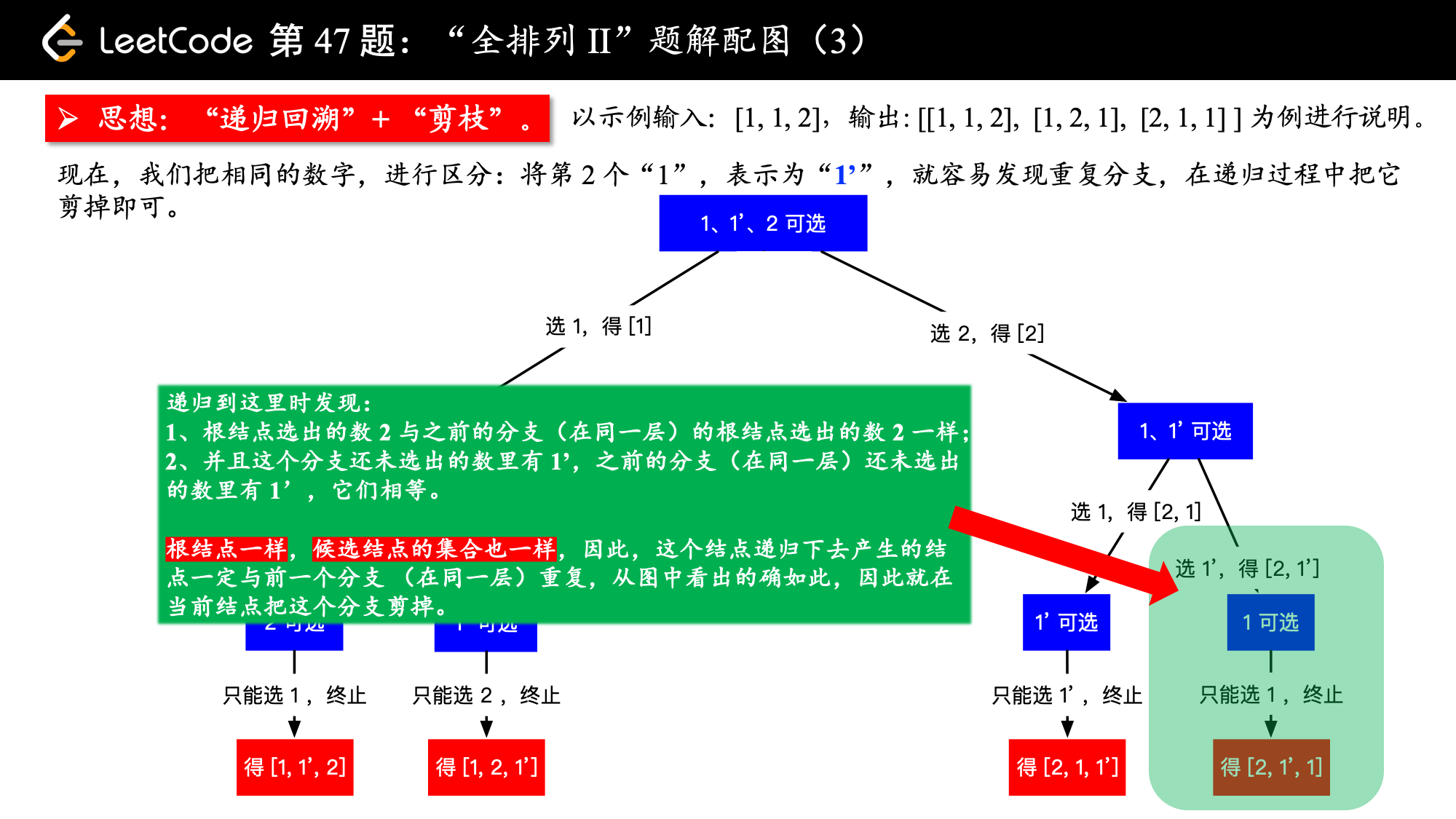
以下代码根据我在「力扣」第 46 题:全排列 II 中的题解(上文有给出链接)中的示例代码修改而来,具体修改的地方,在下面代码的注释中有说明。
基于第 46 题,做 2 处修改即可:
1、在开始回溯算法之前,对数组进行一次排序操作,这是上面多次提到的;
2、在进入一个新的分支之前,看一看这个数是不是和之前的数一样,如果这个数和之前的数一样,并且之前的数还未使用过,那接下来如果走这个分支,就会使用到之前那个和当前一样的数,就会发生重复,此时分支和之前的分支一模一样。(这句话特别关键,可以停下来多看两遍,再看一看上面画的那张图)。
参考代码:
Python 代码:
class Solution:
def permuteUnique(self, nums):
if len(nums) == 0:
return []
# 修改 1:首先排序,之后才有可能发现重复分支
nums.sort()
used = [False] * len(nums)
res = []
self.__dfs(nums, 0, [], used, res)
return res
def __dfs(self, nums, index, pre, used, res):
if index == len(nums):
res.append(pre.copy())
return
for i in range(len(nums)):
if not used[i]:
# 修改 2:因为排序以后重复的数一定不会出现在开始,故 i > 0
# 和之前的数相等,并且之前的数还未使用过,只有出现这种情况,才会出现相同分支
# 这种情况跳过即可
if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:
continue
used[i] = True
pre.append(nums[i])
self.__dfs(nums, index + 1, pre, used, res)
used[i] = False
pre.pop()
if __name__ == '__main__':
s = Solution()
nums = [1, 1, 2]
result = s.permuteUnique(nums)
print(result)
Java 代码:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;
public class Solution {
private List<List<Integer>> res = new ArrayList<>();
private boolean[] used;
private void findPermuteUnique(int[] nums, int depth, Stack<Integer> stack) {
if (depth == nums.length) {
res.add(new ArrayList<>(stack));
return;
}
for (int i = 0; i < nums.length; i++) {
if (!used[i]) {
// 修改 2:因为排序以后重复的数一定不会出现在开始,故 i > 0
// 和之前的数相等,并且之前的数还未使用过,只有出现这种情况,才会出现相同分支
// 这种情况跳过即可
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
used[i] = true;
stack.add(nums[i]);
findPermuteUnique(nums, depth + 1, stack);
stack.pop();
used[i] = false;
}
}
}
public List<List<Integer>> permuteUnique(int[] nums) {
int len = nums.length;
if (len == 0) {
return res;
}
// 修改 1:首先排序,之后才有可能发现重复分支
Arrays.sort(nums);
used = new boolean[len];
findPermuteUnique(nums, 0, new Stack<>());
return res;
}
public static void main(String[] args) {
int[] nums = {1, 1, 2};
Solution solution = new Solution();
List<List<Integer>> permuteUnique = solution.permuteUnique(nums);
System.out.println(permuteUnique);
}
}