LeetCode 第 40 题：“组合总和 II”题解

说明：文本首发在力扣的题解版块，更新也会在第 1 时间在上面的网站中更新，这篇文章只是上面的文章的一个快照，您可以点击上面的链接看到其他网友对本文的评论。

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。解集不能包含重复的组合。示例 1:

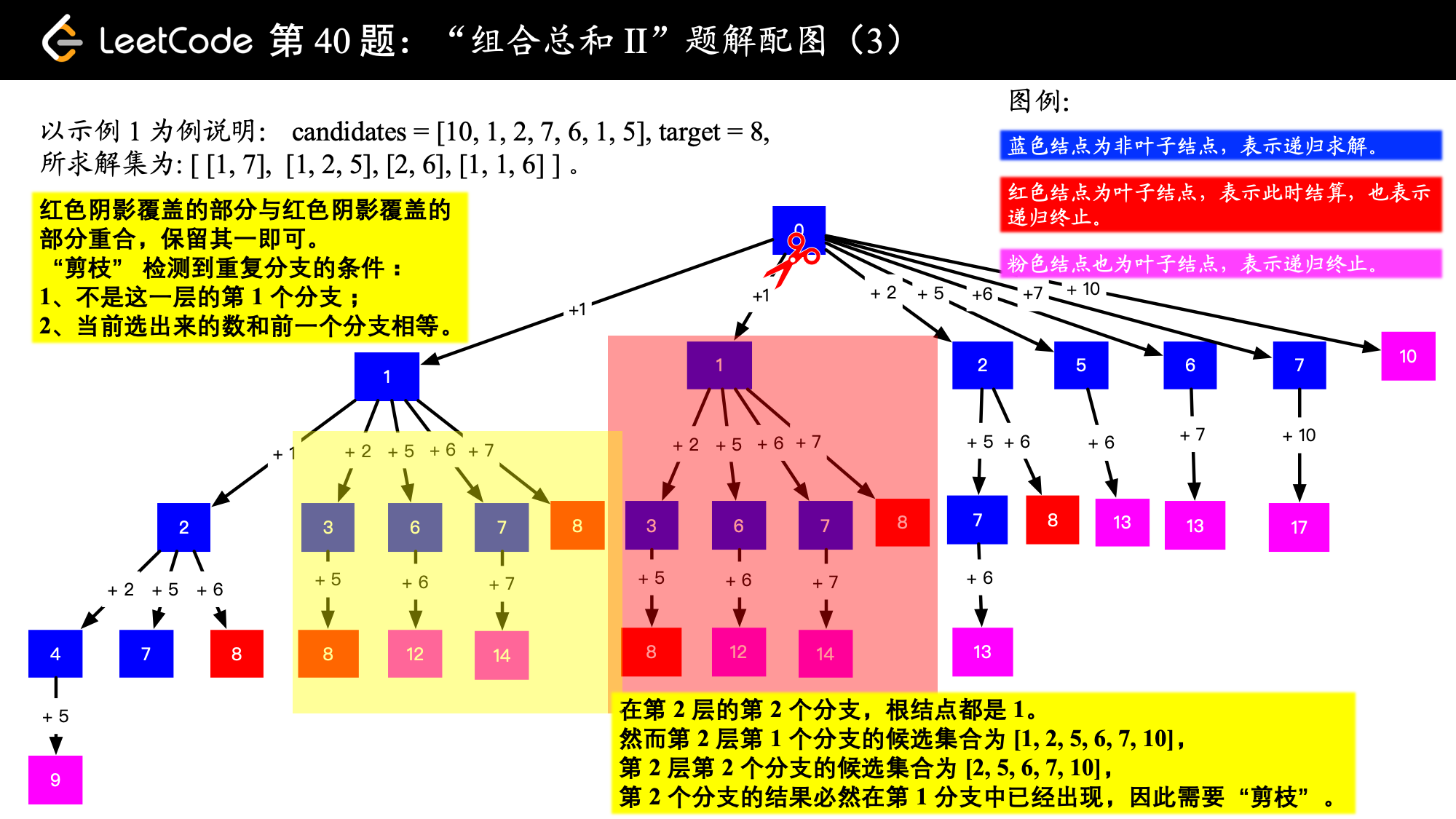
输入: candidates = [10,1,2,7,6,1,5], target = 8, 所求解集为: [ [1, 7], [1, 2, 5], [2, 6], [1, 1, 6] ] 示例 2:

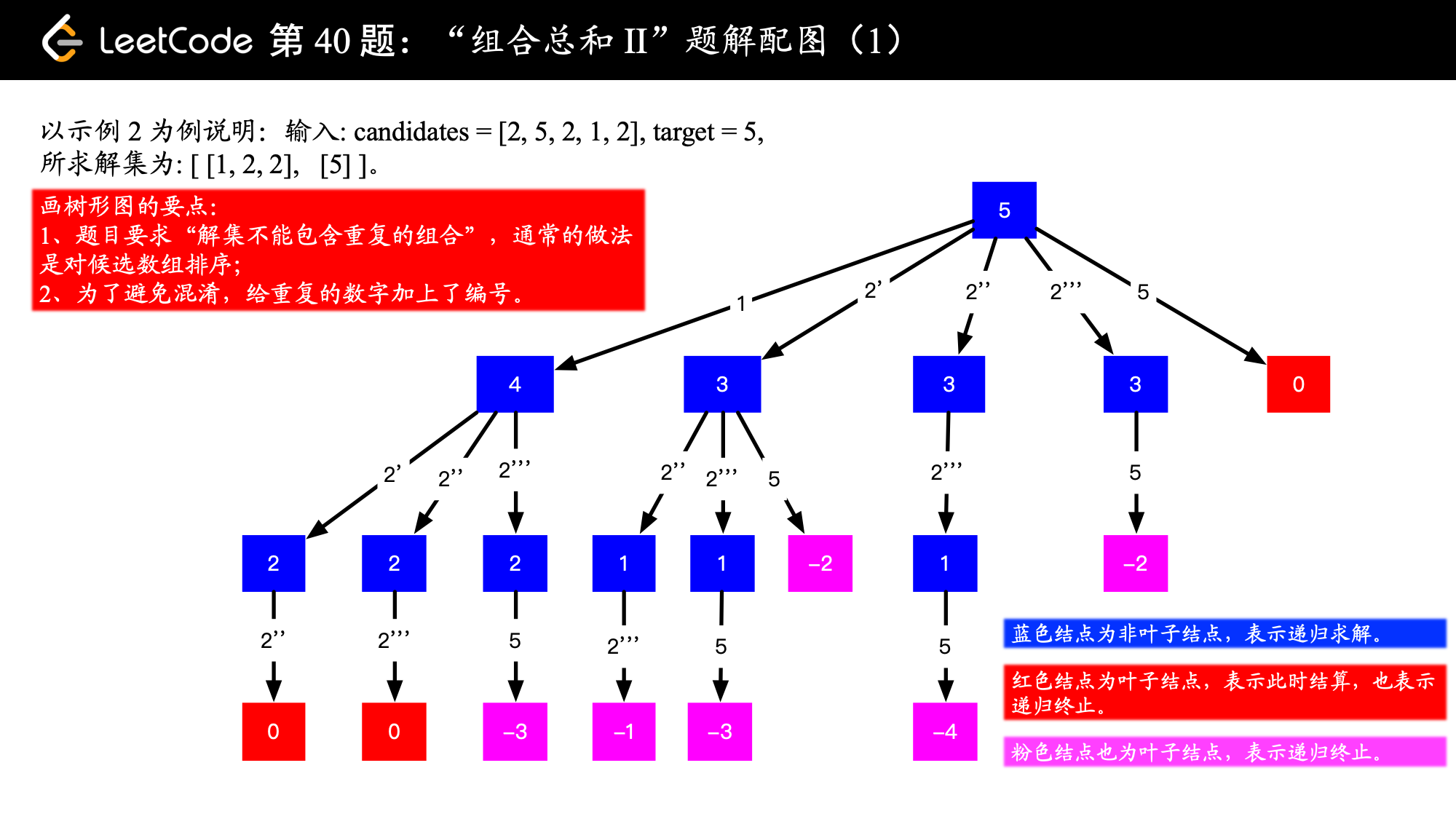
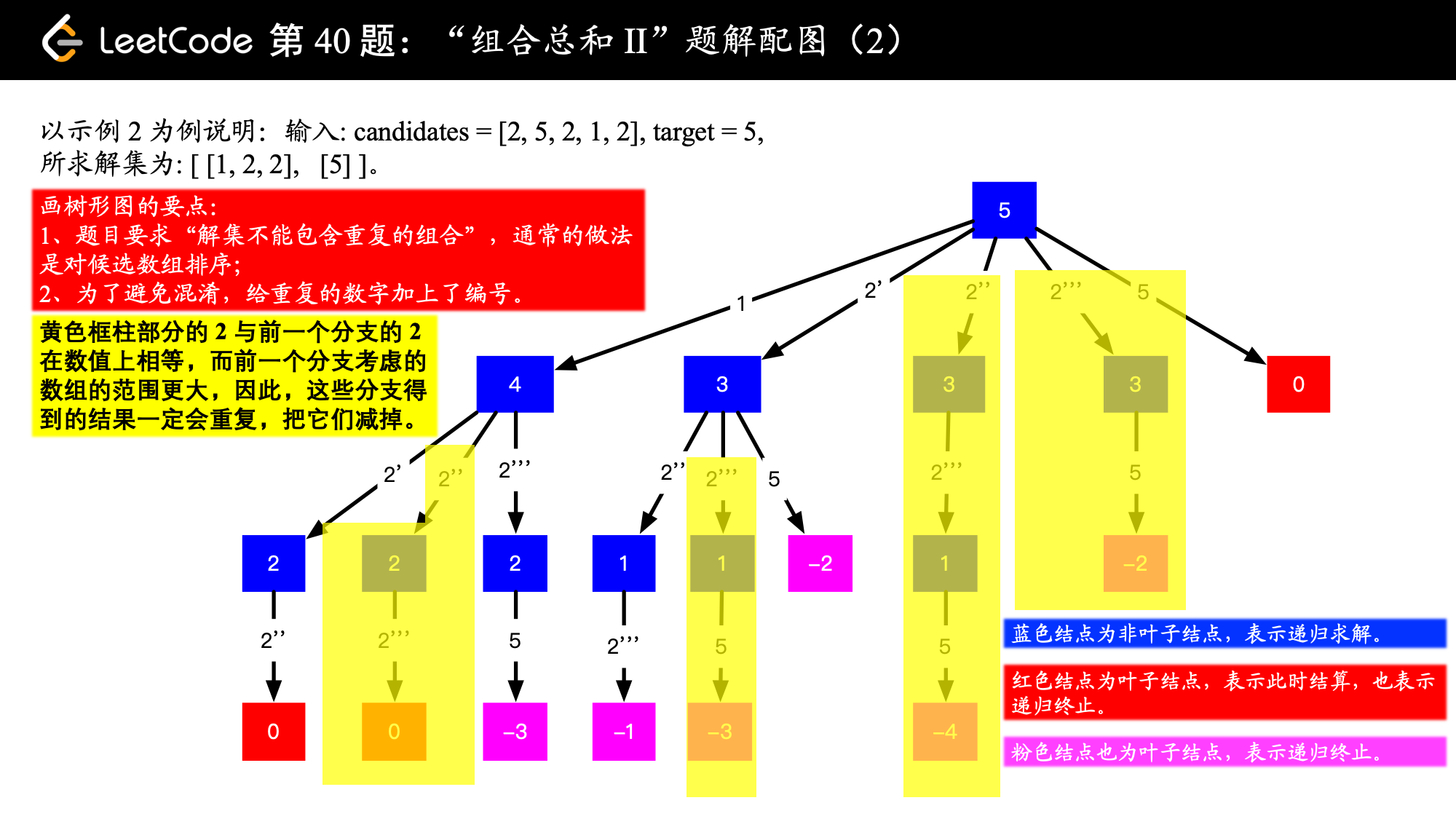
输入: candidates = [2,5,2,1,2], target = 5, 所求解集为: [ [1,2,2], [5] ]

回溯算法 + 剪枝（Python 代码、Java 代码）

这道题与上一问的区别在于：

第 39 题：candidates 中的数字可以无限制重复被选取。
第 40 题：candidates 中的每个数字在每个组合中只能使用一次。

编码的不同，就在于，下一层递归的起始索引不一样。

第 39 题：还从候选数组的当前索引值开始。
第 40 题：从候选数组的当前索引值的下一位开始。

相同之处：解集不能包含重复的组合。

告诉我们对数组先排序是有必要的。

本题解接着它上一个问题的思路。如果读者觉得有必要，可以先阅读我为「力扣」第 39 题：组合总和这道题编写的题解《回溯算法 + 剪枝（Python 代码、Java 代码）》。

思路分析：

这道题其实比上一问更简单，思路是：

以 target 为根结点，依次减去数组中的数字，直到小于 $0$ 或者等于 $0$ ，把等于 $0$ 的结果记录到结果集中。

当然你也可以以 $0$ 为根结点，依次加上数组中的数字，直到大于 target 或者等于 target，把等于 target 的结果记录到结果集中。

“解集不能包含重复的组合”，就暗示我们得对数组先排个序（“升序”或者“降序”均可，下面示例中均使用“升序”）。
“candidates 中的每个数字在每个组合中只能使用一次”，那就按照顺序依次减去数组中的元素，递归求解即可：遇到 $0$ 就结算且回溯，遇到负数也回溯。
candidates 中的数字可以重复，可以借助「力扣」第 47 题：全排列 II 的思想，在搜索的过程中，找到可能发生重复结果的分支，把它剪去。

（温馨提示：下面的幻灯片中，有几页上有较多的文字，可能需要您停留一下，可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。）

参考代码 1：以 target 为根结点，依次减去数组中的数字，直到小于 $0$ 或者等于 $0$ ，把等于 $0$ 的结果记录到结果集中。

Python 代码：

from typing import List


class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        size = len(candidates)
        if size == 0:
            return []
        candidates.sort()
        res = []

        self.__dfs(candidates, size, 0, [], target, res)
        return res

    def __dfs(self, candidates, size, start, path, residue, res):
        if residue == 0:
            res.append(path[:])
            return

        for index in range(start, size):
            if candidates[index] > residue:
                break

            # 剪枝的前提是数组升序排序
            if index > start and candidates[index - 1] == candidates[index]:
                # [1, 1, 2, 5, 6, 7, 10]
                # 0 号索引的 1 ，从后面 6 个元素中搜索
                # 1 号索引也是 1 ，从后面 5 个元素（是上面 6 个元素的真子集）中搜索，这种情况显然上面已经包含
                continue

            path.append(candidates[index])
            # 这里要传入 index + 1，因为当前元素不能被重复使用
            # 如果 index + 1 越界，传递到下一个方法中，什么也不执行
            self.__dfs(candidates, size, index + 1, path, residue - candidates[index], res)
            path.pop()

Java 代码：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;

public class Solution {


    // residue 表示剩余，这个值一开始等于 target，基于题目中说明的"所有数字（包括目标数）都是正整数"这个条件
    // residue 在递归遍历中，只会越来越小
    private void findCombinationSum2(int[] candidates, int begin, int len, int residue, Stack<Integer> stack, List<List<Integer>> res) {
        if (residue == 0) {
            res.add(new ArrayList<>(stack));
            return;
        }
        for (int i = begin; i < len && residue - candidates[i] >= 0; i++) {
            // 这一步之所以能够生效，其前提是数组一定是排好序的，这样才能保证：
            // 在递归调用的统一深度（层）中，一个元素只使用一次。
            // 这一步剪枝操作基于 candidates 数组是排序数组的前提下
            if (i > begin && candidates[i] == candidates[i - 1]) {
                continue;
            }
            stack.add(candidates[i]);
            // 【关键】因为元素不可以重复使用，这里递归传递下去的是 i + 1 而不是 i
            findCombinationSum2(candidates, i + 1, len, residue - candidates[i], stack, res);
            stack.pop();
        }
    }

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }
        // 先将数组排序，这一步很关键
        Arrays.sort(candidates);
        findCombinationSum2(candidates, 0, len, target, new Stack<>(), res);
        return res;
    }

    public static void main(String[] args) {
        int[] candidates = {10, 1, 2, 7, 6, 1, 5};
        int target = 8;
        Solution solution = new Solution();
        List<List<Integer>> combinationSum2 = solution.combinationSum2(candidates, target);
        System.out.println(combinationSum2);
    }
}

这里按照用户 @Aspire 提供的思路，给出从 $0$ 开始，一个使用加法，搜索加到目标数的写法，“前提是排序（升序降序均可）”，然后“剪枝”的操作和上面一样。

参考代码 2：以 $0$ 为根结点，依次加上数组中的数字，直到大于 target 或者等于 target，把等于 target 的结果记录到结果集中。

C++ 代码：

#include <iostream>
#include <vector>
#include <map>

using namespace std;

class Solution {
public:

    vector<int> input;
    int target;
    vector<vector<int>> result;
    vector<int> vc;

    void dfs(int index, int sum) {
        // index >= input.size() ，写成 index == input.size() 即可
        // 因为每次都 + 1，在 index == input.size() 剪枝就可以了
        if (sum >= target || index == input.size()) {
            if (sum == target) {
                result.push_back(vc);
            }
            return;
        }
        for (int i = index; i < input.size(); i++) {
            if (input[i] > target) {
                continue;
            }

            // 【我添加的代码在这里】：
            // 1、i > index 表明剪枝的分支一定不是当前层的第 1 个分支
            // 2、input[i - 1] == input[i] 表明当前选出来的数等于当前层前一个分支选出来的数
            // 因为前一个分支的候选集合一定大于后一个分支的候选集合
            // 故后面出现的分支中一定包含了前面分支出现的结果，因此剪枝
            // “剪枝”的前提是排序，升序或者降序均可
            if (i > index && input[i - 1] == input[i]) {
                continue;
            }

            vc.push_back(input[i]);
            sum += input[i];
            dfs(i + 1, sum);
            vc.pop_back();
            sum -= input[i];
        }
    }

    vector<vector<int>> combinationSum2(vector<int> &candidates, int target) {
        // “剪枝”的前提是排序，升序或者降序均可
        sort(candidates.begin(), candidates.end());
        this->input = candidates;
        this->target = target;
        dfs(0, 0);
        return result;
    }
};


int main() {
    cout << "LeetCode 第 40 题：组合问题 II" << endl;
    Solution solution = Solution();

    vector<int> candidates;
    candidates.push_back(10);
    candidates.push_back(1);
    candidates.push_back(2);
    candidates.push_back(7);
    candidates.push_back(6);
    candidates.push_back(1);
    candidates.push_back(5);

    int target = 8;
    vector<vector<int>> res = solution.combinationSum2(candidates, target);
    for (int i = 0; i < res.size(); ++i) {
        for (int j = 0; j < res[i].size(); ++j) {
            cout << res[i][j] << ",";
        }
        cout << "" << endl;
    }
    return 0;
}

← LeetCode 第 39 题：“组合总和”题解 LeetCode 第 46 题：“全排列”题解 →

# LeetCode 第 40 题：“组合总和 II”题解

# 回溯算法 + 剪枝（Python 代码、Java 代码）

#

LeetCode 第 40 题：“组合总和 II”题解

回溯算法 + 剪枝（Python 代码、Java 代码）