LeetCode 第 77 题：“组合”题解

题解地址：回溯算法 + 剪枝（Python 代码、Java 代码）。

说明：文本首发在力扣的题解版块，更新也会在第 1 时间在上面的网站中更新，这篇文章只是上面的文章的一个快照，您可以点击上面的链接看到其他网友对本文的评论。

传送门：77. 组合。

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

回溯算法 + 剪枝（Python 代码、Java 代码）

方法：回溯

和全排列问题一样，这是一道使用回溯算法解决的经典问题。而分析回溯问题，我们常常需要画图来帮助我们理清思路和寻找边界条件。

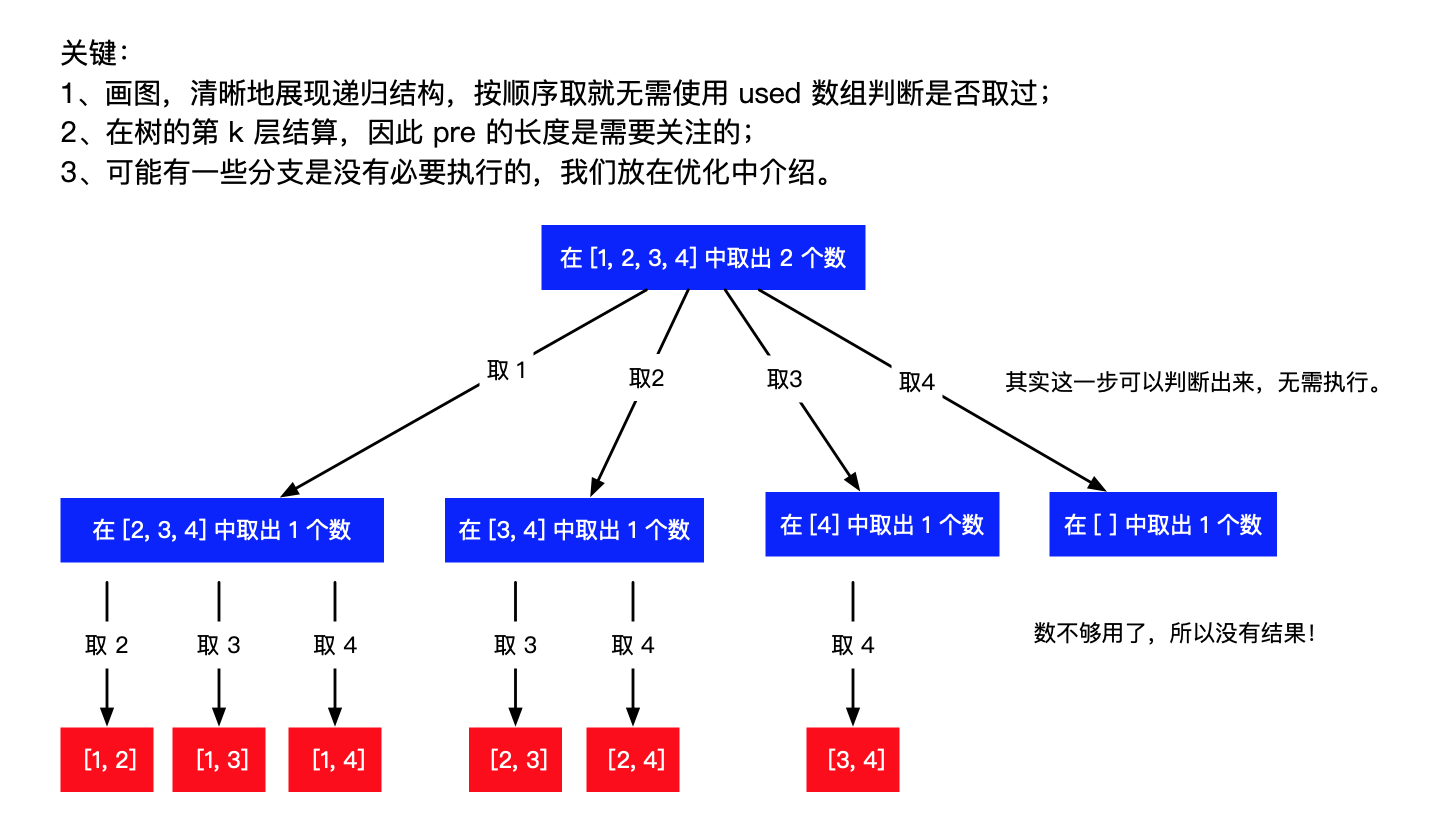
参考代码：

Python 代码：

from typing import List


class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        # 先把不符合条件的情况去掉
        if n <= 0 or k <= 0 or k > n:
            return []
        res = []
        self.__dfs(1, k, n, [], res)
        return res

    def __dfs(self, start, k, n, pre, res):
        # 当前已经找到的组合存储在 pre 中，需要从 start 开始搜索新的元素
        # 在第 k 层结算
        if len(pre) == k:
            res.append(pre[:])
            return

        for i in range(start, n + 1):
            pre.append(i)
            # 因为已经把 i 加入到 pre 中，下一轮就从 i + 1 开始
            # 注意和全排列问题的区别，因为按顺序选择，因此无须使用 used 数组
            self.__dfs(i + 1, k, n, pre, res)
            # 回溯的时候，状态重置
            pre.pop()

Java 代码：

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class Solution {

    private List<List<Integer>> res = new ArrayList<>();

    private void findCombinations(int n, int k, int begin, Stack<Integer> pre) {
        if (pre.size() == k) {
            // 够数了，就添加到结果集中
            res.add(new ArrayList<>(pre));
            return;
        }
        // 关键在于分析出 i 的上界
        for (int i = begin; i <= n; i++) {
            pre.add(i);
            findCombinations(n, k, i + 1, pre);
            pre.pop();
        }
    }

    public List<List<Integer>> combine(int n, int k) {
        // 特判
        if (n <= 0 || k <= 0 || n < k) {
            return res;
        }
        // 从 1 开始是题目的设定
        findCombinations(n, k, 1, new Stack<>());
        return res;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        List<List<Integer>> combine = solution.combine(4, 2);
        System.out.println(combine);
    }
}

这个方法，我们遗留了一个问题，那就是我们感觉有些分支没有必要执行，那就是每一层最后要执行的那些分支，下面我们具体研究一下这个问题。

优化：剪枝

当然画图分析还是法宝。

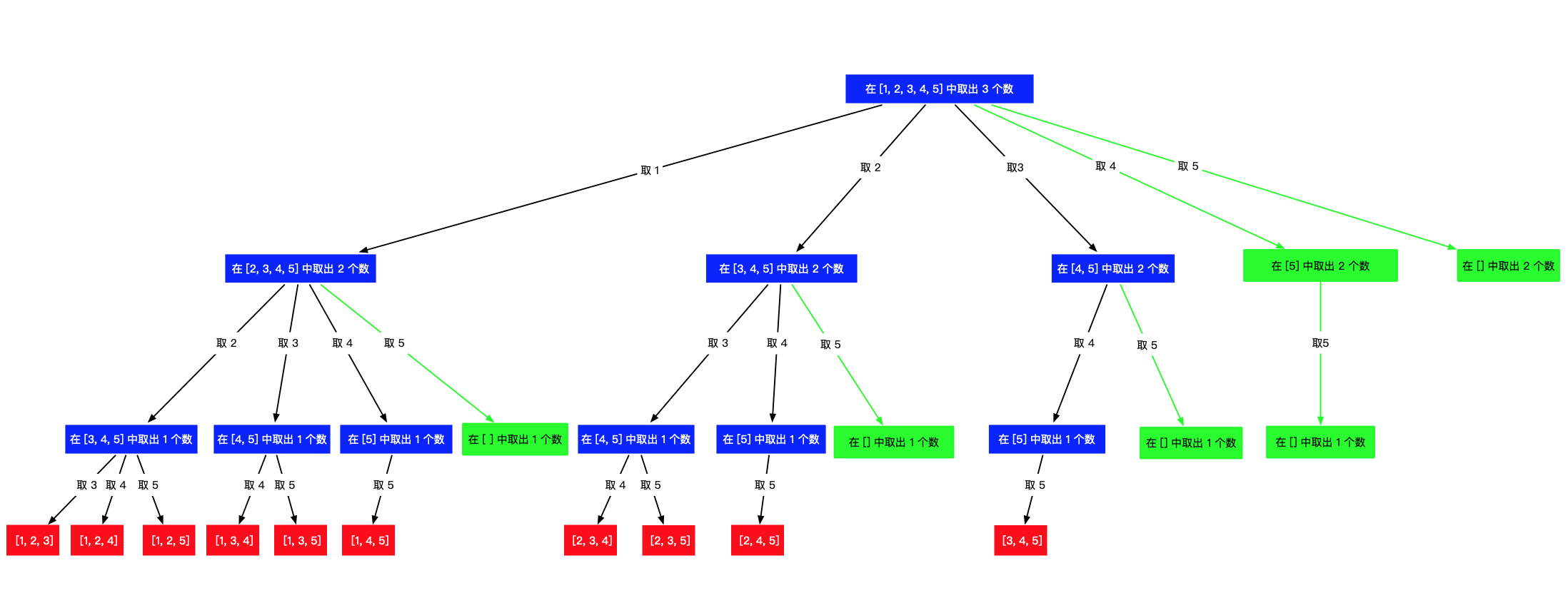
其中绿色的部分，是不能产生结果的分支，但是我们的代码确实又执行到了这部分。

上面的代码中，我们发现：其实如果 pre 已经选择到 [1,4,5] 或者 [2,4,5] 或者 [3,4,5] ，后序的代码就没有必要执行，继续走也不能发现新的满足题意的组合。干了类似于下面事情，其实有很多步骤是多余的：选择了 [1,4,5] 以后， 5 弹出 [1,4,5] 成为 [1,4] ,4 弹出 [1,4] 成为 4 ，然后 5 进来，成为 [1,5]，在进来发现 for 循环都进不了（因为没有可选的元素），然后 5 又弹出，接着 1 弹出。

发现多余操作：那么我们如何发现多余的步骤呢，其实也是有规律可寻的，就在 for 循环中：

for (int i = start; i <= n; i++) {
    pre.add(i);
    generateCombinations(n, k, i + 1, pre);
    pre.remove(pre.size() - 1);
}

这个函数干的事情，是从 [i, n] 这个区间里（注意，左右都是闭区间），找到 k - pre.zize() 个元素。 i <= n 不是每一次都要走完的， i 有一个上限。

寻找规律：我们再看图，可以发现一些边界情况，帮助我们发现规律:

当选定了一个元素，即 pre.size() == 1 的时候，接下来要选择 2 个元素， i 最大的值是 4 ，因为从 5 开始选择，就无解了；
当选定了两个元素，即 pre.size() == 2 的时候，接下来要选择 1 个元素， i 最大的值是 5 ，因为从 6 开始选择，就无解了。

再如：如果 n = 6 ，k = 4，
pre.size() == 1 的时候，接下来要选择 3 个元素， i 最大的值是 4，最后一个被选的是 [4,5,6]；
pre.size() == 2 的时候，接下来要选择 2 个元素， i 最大的值是 5，最后一个被选的是 [5,6]；
pre.size() == 3 的时候，接下来要选择 1 个元素， i 最大的值是 6，最后一个被选的是 [6]；

再如：如果 n = 15 ，k = 4，
pre.size() == 1 的时候，接下来要选择 3 个元素，i 最大的值是 13，最后一个被选的是 [13,14,15]；
pre.size() == 2 的时候，接下来要选择 2 个元素， i 最大的值是 14，最后一个被选的是 [14,15]；
pre.size() == 3 的时候，接下来要选择 1 个元素， i 最大的值是 15，最后一个被选的是 [15]；

多写几遍（发现 max(i) 是我们倒着写出来），我么就可以发现 max(i) 与接下来要选择的元素貌似有一点关系，很容易知道： max(i) + 接下来要选择的元素个数 - 1 = n，其中，接下来要选择的元素个数 = k - pre.size()，整理得到：

max(i) = n - (k - pre.size()) + 1

所以，我们的剪枝过程就是：把 i <= n 改成 i <= n - (k - pre.size()) + 1 ：

参考代码：

Python 代码：

from typing import List


class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        # 特判
        if n <= 0 or k <= 0 or k > n:
            return []
        res = []
        self.__dfs(1, k, n, [], res)
        return res

    def __dfs(self, start, k, n, pre, res):
        if len(pre) == k:
            res.append(pre[:])
            return

        # 注意：这里 i 的上限是归纳得到的
        for i in range(start, n - (k - len(pre)) + 2):
            pre.append(i)
            self.__dfs(i + 1, k, n, pre, res)
            pre.pop()

Java 代码：

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

// 剪枝优化版本：
public class Solution3 {

    private List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
        if (n <= 0 || k <= 0 || n < k) {
            return result;
        }
        findCombinations(n, k, 1, new Stack<>());
        return result;
    }

    // p 可以声明成一个栈
    // i 的极限值满足： n - i + 1 = (k - pre.size())。
    // 【关键】n - i + 1 是闭区间 [i,n] 的长度。
    // k - pre.size() 是剩下还要寻找的数的个数。
    private void findCombinations(int n, int k, int index, Stack<Integer> p) {
        if (p.size() == k) {
            result.add(new ArrayList<>(p));
            return;
        }
        for (int i = index; i <= n - (k - p.size()) + 1; i++) {
            p.push(i);
            findCombinations(n, k, i + 1, p);
            p.pop();
        }
    }

    public static void main(String[] args) {
        List<List<Integer>> lists = new Solution3().combine(4, 2);
        System.out.println(lists);
    }
}

← LeetCode 第 60 题：“第 k 个排列”题解 LeetCode 第 78 题：“子集”题解 →

# LeetCode 第 77 题：“组合”题解

# 回溯算法 + 剪枝（Python 代码、Java 代码）

# 方法：回溯

# 优化：剪枝

LeetCode 第 77 题：“组合”题解

回溯算法 + 剪枝（Python 代码、Java 代码）

方法：回溯

优化：剪枝