LeetCode 第 39 题:“组合总和”题解
题解地址:回溯算法 + 剪枝(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:39. 组合总和。
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。 解集不能包含重复的组合。 示例 1:
输入: candidates = [2,3,6,7], target = 7, 所求解集为: [ [7], [2,2,3] ] 示例 2:
输入: candidates = [2,3,5], target = 8, 所求解集为: [ [2,2,2,2], [2,3,3], [3,5] ]
回溯算法 + 剪枝(Python 代码、Java 代码)
做搜索、回溯问题的套路是画图,代码其实就是根据画出的树形图写出来的。
思路分析:
那么如何画图呢?
- 根据题目中的用例,画一个图,因为是搜索,因此呈现的是一个树形结构图,并且在这个树形结构中会体现出递归结构。
- 根据题目中的用例,比对自己画图的结果和题目的结果的差异,如果一样,说明我们的分析没有错;如果不一样,说明我们的分析有误,一定有哪一个环节漏掉了或者分析错误,根据找到的问题调整算法。
下面我具体说一下,本来想展示草稿的,奈何本人画的图太难看,还是用软件画图给大家看吧。
针对示例 1:
输入:
candidates = [2, 3, 6, 7],target = 7, 所求解集为:[[7], [2, 2, 3]]
一开始我画的图是这样的:
思路:以 target = 7 为根结点,每一个分支做减法。减到 或者负数的时候,剪枝。其中,减到 的时候结算,这里“结算”的意思是添加到结果集。
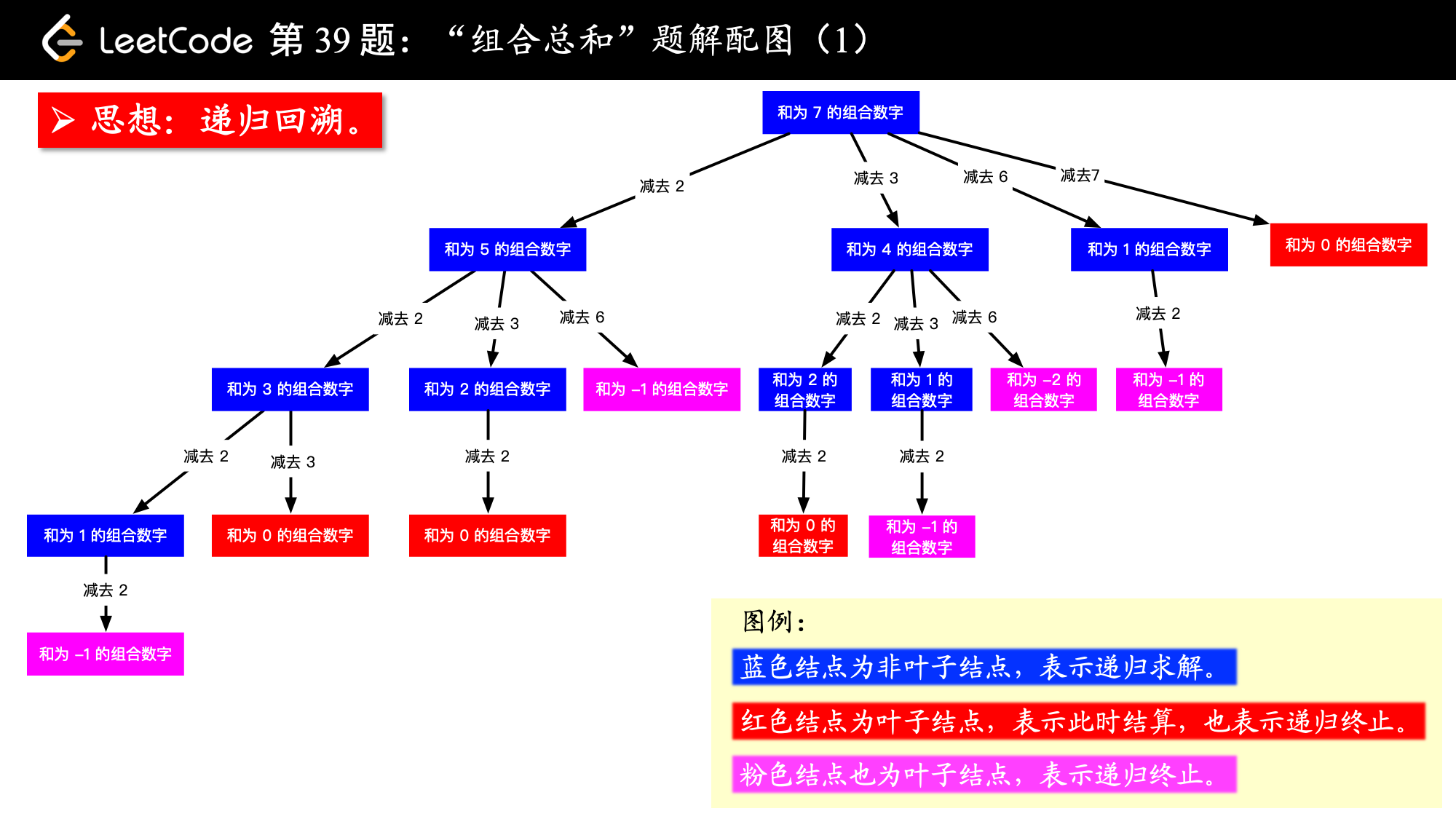
我把其中文字的部分去掉了,这样大家看得清楚一点:
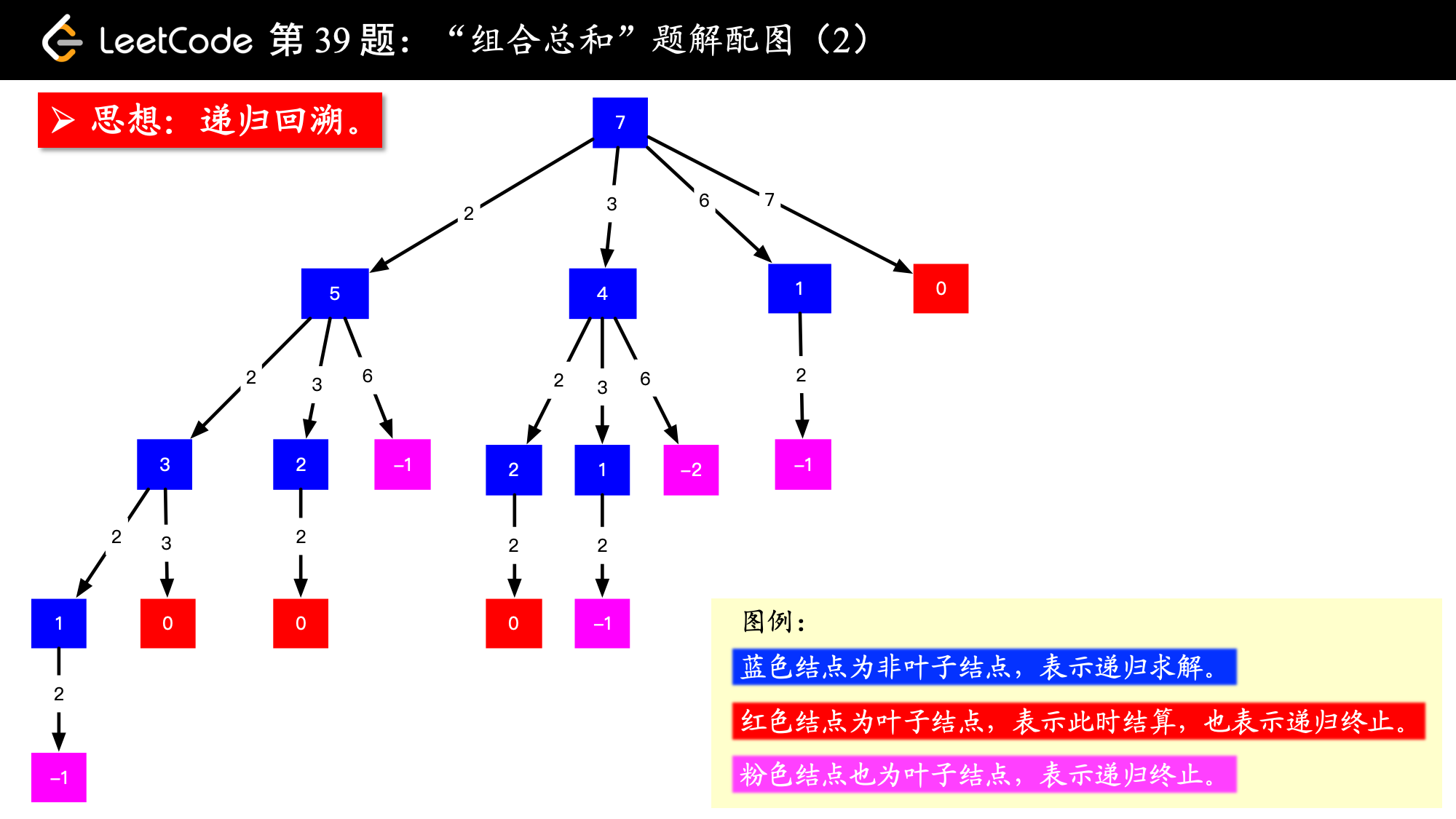
说明:
1、一个蓝色正方形表示的是“尝试将这个数到数组 candidates 中找组合”,那么怎么找呢?挨个减掉那些数就可以了。
2、在减的过程中,会得到 和负数,也就是被我标红色和粉色的结点:
- 得到 是我们喜欢的,从 这一点向根结点走的路径(很可能只走过一条边,也算一个路径),就是一个组合,在这一点要做一次结算(把根结点到 所经过的路径,加入结果集)。
- 得到负数就说明这条路走不通,没有必要再走下去了。
总结一下:在减的过程中,得到 或者负数,就没有必要再走下去,所以这两种情况就分别表示成为叶子结点。此时递归结束,然后要发生回溯。
画出图以后,我看了一下,我这张图画出的结果有 个 ,对应的路径是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]] ,而示例中的解集只有 [[7], [2, 2, 3]],很显然,我的分析出现了问题。问题是很显然的,我的结果集出现了重复。重复的原因是
后面分支的更深层的边出现了前面分支低层的边的值。
限于我的表达能力有限,大伙意会这句话就可以了,看一看重复的叶子结点 的路径,想一想重复的原因,或许你会比我说得更清楚更好。
但是这个问题也不难解决,把候选数组排个序就好了(想一下,结果数组排个序是不是也可以去重),后面选取的数不能比前面选的数还要小,即“更深层的边上的数值不能比它上层的边上的数值小”,按照这种策略,剪枝就可以去掉重复的组合。
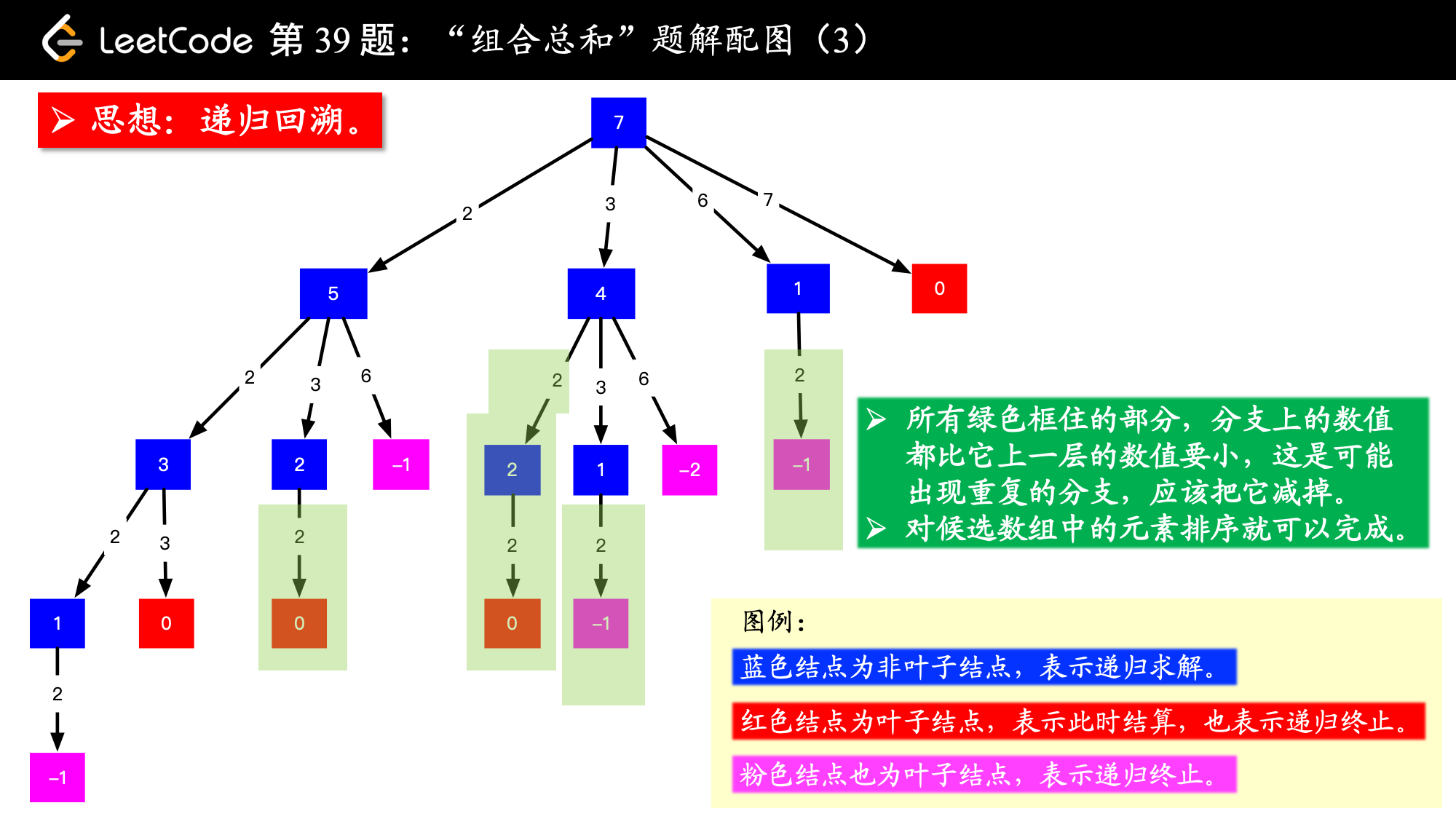
参考代码 1:
Python 代码:
from typing import List
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
size = len(candidates)
if size == 0:
return []
# 剪枝的前提是数组元素排序
# 深度深的边不能比深度浅的边还小
# 要排序的理由:1、前面用过的数后面不能再用;2、下一层边上的数不能小于上一层边上的数。
candidates.sort()
# 在遍历的过程中记录路径,一般而言它是一个栈
path = []
res = []
# 注意要传入 size ,在 range 中, size 取不到
self.__dfs(candidates, 0, size, path, res, target)
return res
def __dfs(self, candidates, begin, size, path, res, target):
# 先写递归终止的情况
if target == 0:
res.append(path[:])
for index in range(begin, size):
residue = target - candidates[index]
if residue < 0:
break
path.append(candidates[index])
# 因为下一层不能比上一层还小,索引起始还从 index 开始
self.__dfs(candidates, index, size, path, res, residue)
path.pop()
if __name__ == '__main__':
candidates = [2, 3, 6, 7]
target = 7
solution = Solution()
result = solution.combinationSum(candidates, target)
print(result)
Java 代码:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;
public class Solution {
private List<List<Integer>> res = new ArrayList<>();
private int[] candidates;
private int len;
private void findCombinationSum(int residue, int start, Stack<Integer> pre) {
if (residue == 0) {
res.add(new ArrayList<>(pre));
return;
}
// 优化添加的代码2:在循环的时候做判断,尽量避免系统栈的深度
// residue - candidates[i] 表示下一轮的剩余,如果下一轮的剩余都小于 0 ,就没有必要进行后面的循环了
// 这一点基于原始数组是排序数组的前提,因为如果计算后面的剩余,只会越来越小
for (int i = start; i < len && residue - candidates[i] >= 0; i++) {
pre.add(candidates[i]);
// 【关键】因为元素可以重复使用,这里递归传递下去的是 i 而不是 i + 1
findCombinationSum(residue - candidates[i], i, pre);
pre.pop();
}
}
public List<List<Integer>> combinationSum(int[] candidates, int target) {
int len = candidates.length;
if (len == 0) {
return res;
}
// 优化添加的代码1:先对数组排序,可以提前终止判断
Arrays.sort(candidates);
this.len = len;
this.candidates = candidates;
findCombinationSum(target, 0, new Stack<>());
return res;
}
public static void main(String[] args) {
int[] candidates = {2, 3, 6, 7};
int target = 7;
Solution solution = new Solution();
List<List<Integer>> combinationSum = solution.combinationSum(candidates, target);
System.out.println(combinationSum);
}
}
补充:事实上,不排序也是可以的,只要保证按顺序读取,也可以通过测试用例,所以剪枝的前提还是对候选数组进行排序。
我个人还是觉得排序更好一些,这样“剪枝”工作可以更彻底一些,并且排序可以“倒序排序”,这样生成的递归树可能会更矮一些。(这个观点待讨论)
参考代码 2:
Python 代码:
from typing import List
# 不排序的写法,只有遇到减到负数的时候剪枝
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
size = len(candidates)
if size == 0:
return []
res = []
self.__dfs(candidates, size, 0, [], target, res)
return res
def __dfs(self, candidates, size, start, path, residue, res):
if residue < 0:
return
if residue == 0:
res.append(path[:])
return
for index in range(start, size):
path.append(candidates[index])
# 注意:因为数字可以无限制重复被选取,因此起始位置还是自己
self.__dfs(candidates, size, index, path, residue - candidates[index], res)
path.pop()
if __name__ == '__main__':
candidates = [2, 3, 6, 7]
target = 7
solution = Solution()
result = solution.combinationSum(candidates, target)
print(result)
Java 代码:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;
public class Solution {
private List<List<Integer>> res = new ArrayList<>();
private int[] candidates;
private int len;
private void findCombinationSum(int residue, int start, Stack<Integer> pre) {
if (residue < 0) {
return;
}
if (residue == 0) {
res.add(new ArrayList<>(pre));
return;
}
for (int i = start; i < len; i++) {
pre.add(candidates[i]);
findCombinationSum(residue - candidates[i], i, pre);
pre.pop();
}
}
public List<List<Integer>> combinationSum(int[] candidates, int target) {
int len = candidates.length;
if (len == 0) {
return res;
}
this.len = len;
this.candidates = candidates;
findCombinationSum(target, 0, new Stack<>());
return res;
}
public static void main(String[] args) {
int[] candidates = {2, 3, 6, 7};
int target = 7;
Solution3 solution = new Solution3();
List<List<Integer>> combinationSum = solution.combinationSum(candidates, target);
System.out.println(combinationSum);
}
}
附注:这道题我用的是减法,有兴趣的朋友还可以使用加法,加到 target 的时候结算,超过 target 的时候剪枝。
做完这题的朋友,不妨做一下 LeetCode 第 40 题:组合问题 II。