LeetCode 第 60 题：“第 k 个排列”题解

说明：文本首发在力扣的题解版块，更新也会在第 1 时间在上面的网站中更新，这篇文章只是上面的文章的一个快照，您可以点击上面的链接看到其他网友对本文的评论。

给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

"123" "132" "213" "231" "312" "321" 给定 n 和 k，返回第 k 个排列。

说明：

给定 n 的范围是 [1, 9]。给定 k 的范围是[1, n!]。示例 1:

输入: n = 3, k = 3 输出: "213" 示例 2:

输入: n = 4, k = 9 输出: "2314"

回溯 + 剪枝（Python 代码、Java 代码）

思路分析：

比较容易想到的是，使用同「力扣」第 46 题：全排列，即使用回溯的思想，依次得到全排列，输出所求的第 $k$ 个全排列即可。但事实上，我们不必求出所有的全排列。基于以下几点考虑：

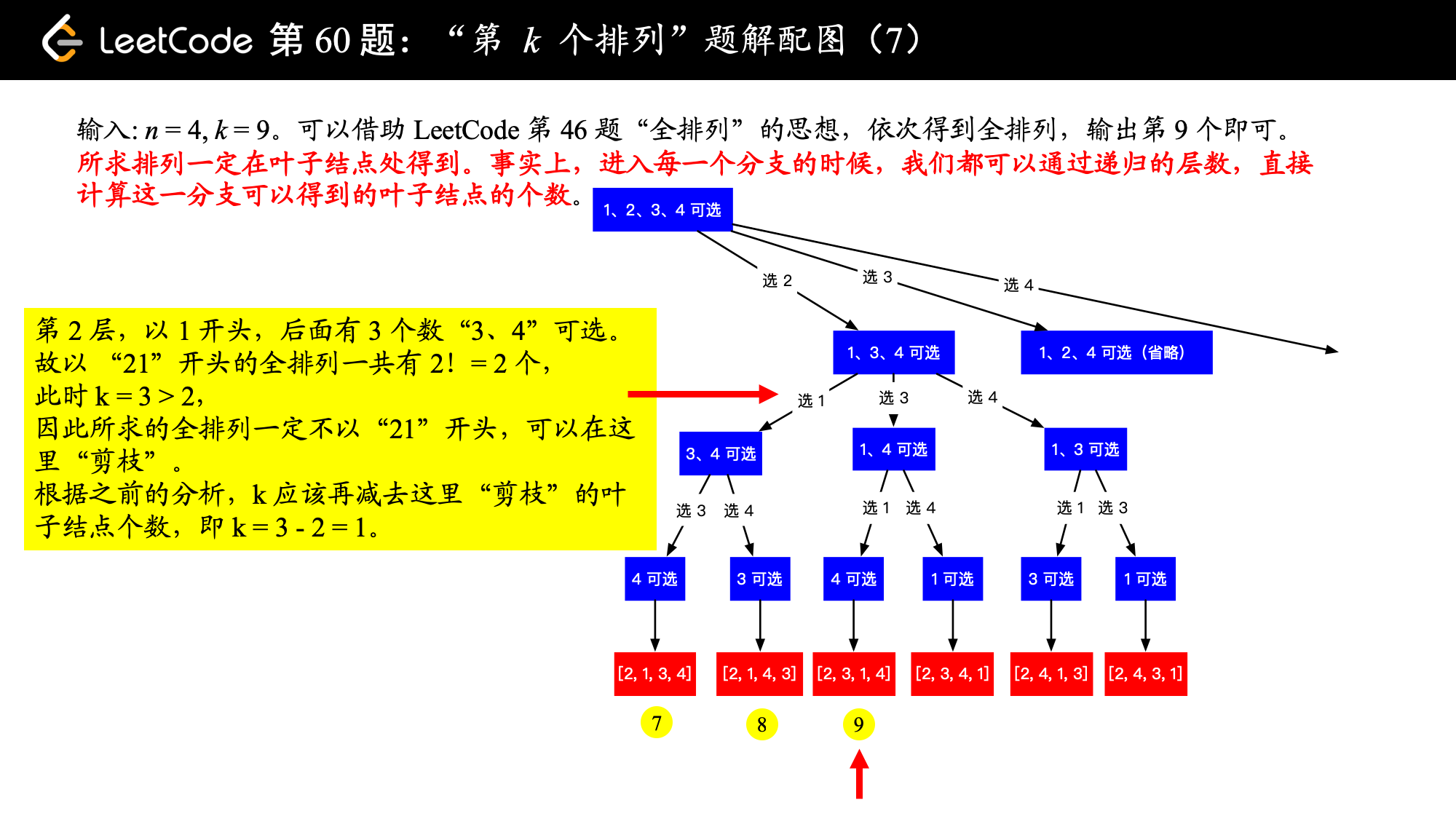
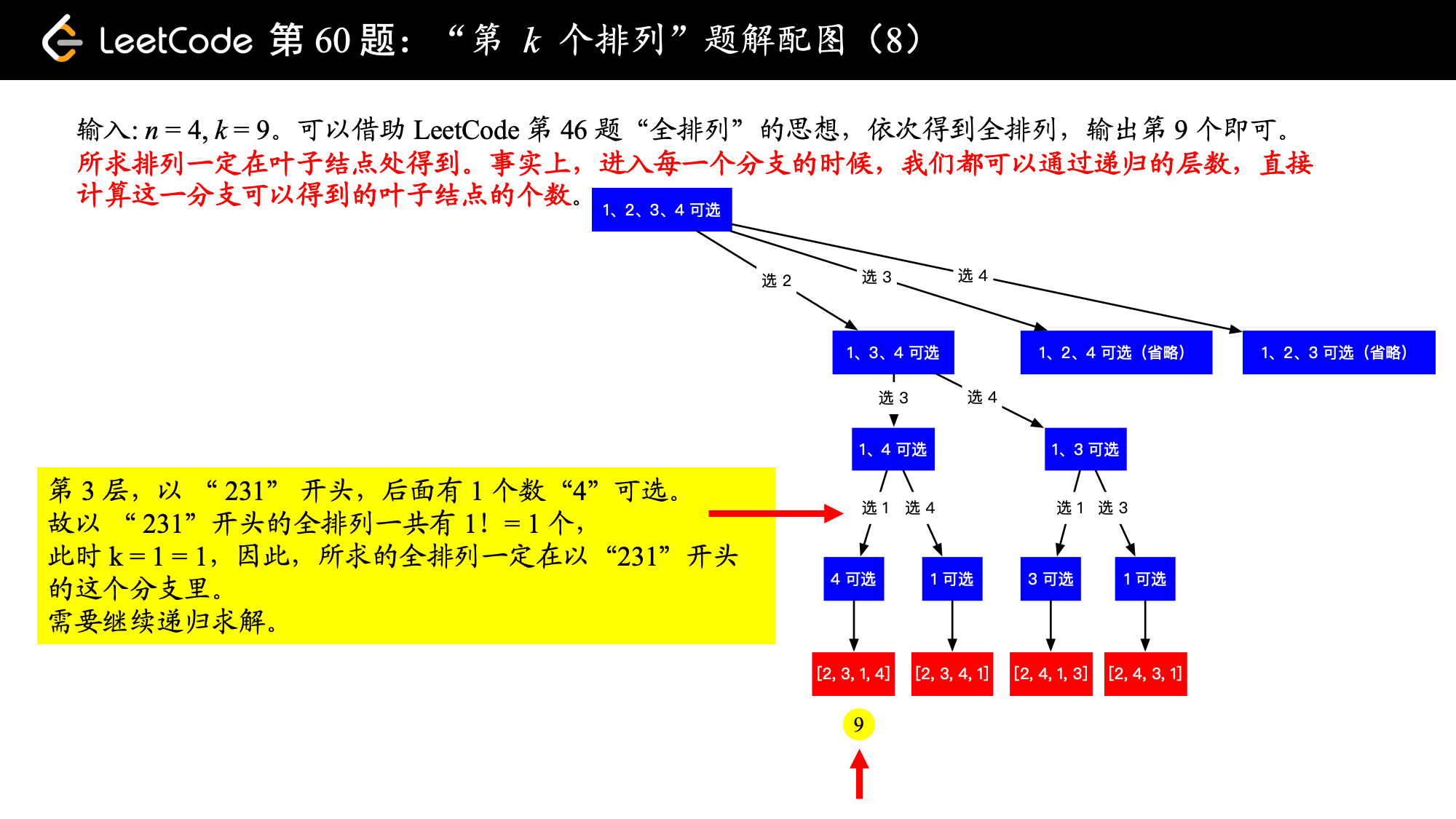
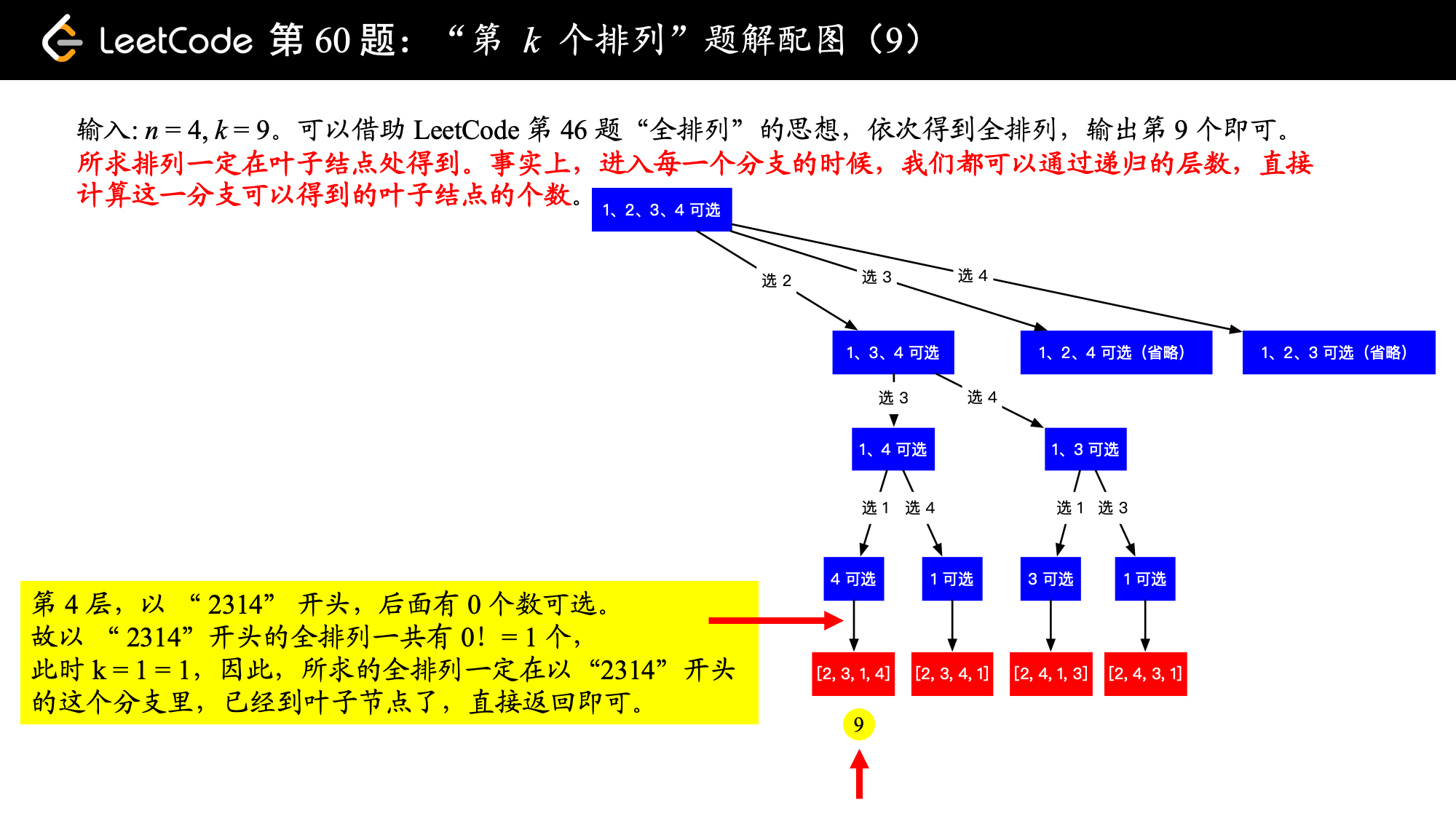
1、我们知道所求排列一定在叶子结点处得到。事实上，进入每一个分支的时候，我们都可以通过递归的层数，直接计算这一分支可以得到的叶子结点的个数。

这是因为：进入一个分支的时候，我们可以根据已经选定的数的个数，进而确定还未选定的数的个数，然后计算阶乘，就知道这一个分支的叶子结点有多少个。

2、如果 $k$ 大于这一个分支将要产生的叶子结点数，直接跳过这个分支，即“剪枝”即可。

这是因为：即使你回溯去做，要设置状态，回溯回来的时候状态还要重置，但其实跳过的这个分支的叶子结点具体是啥我们并不关心。

3、如果 $k$ 小于等于这一个分支将要产生的叶子结点数，那说明所求的全排列一定在这一个分支将要产生的叶子结点里，需要递归求解。

4、计算阶乘的时候，你可以使用循环计算，特别注意： $0!=1$ ，它表示了没有数可选的时候，即表示到达叶子结点了，排列数只剩下 $1$ 个。

又因为题目中说“给定 $n$ 的范围是 $[1, 9]$ ”，故可以实现把从 $0$ 到 $9$ 的阶乘计算好，放在一个数组里，可以根据索引直接获得阶乘值，见文后“代码 2”。

下面以示例 2：输入: $n = 4$ ， $k = 9$ ，介绍如何使用“回溯 + 剪枝” 的思想得到输出 "2314"。

（温馨提示：下面的幻灯片中，有几页上有较多的文字，可能需要您停留一下，可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。）

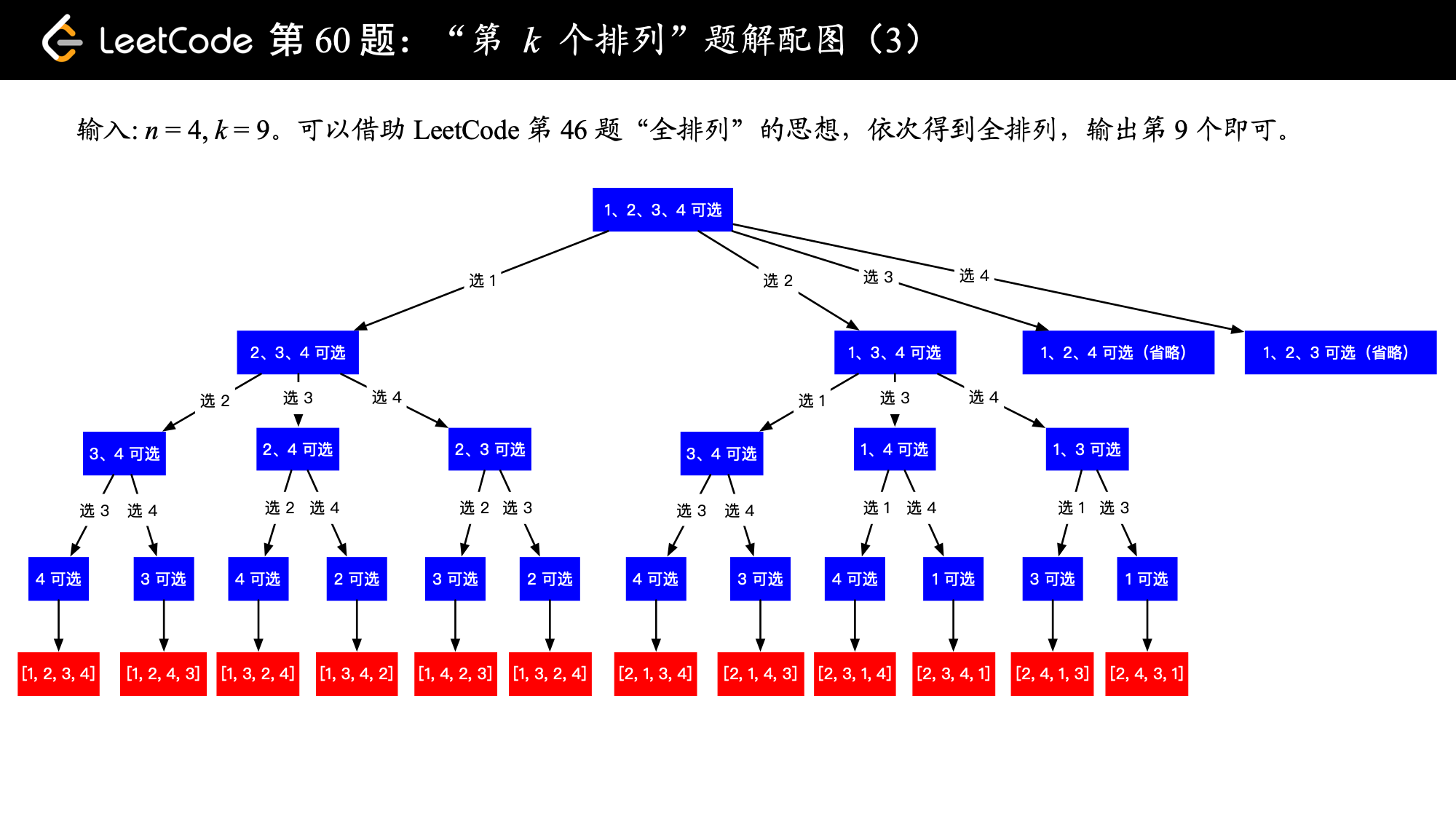
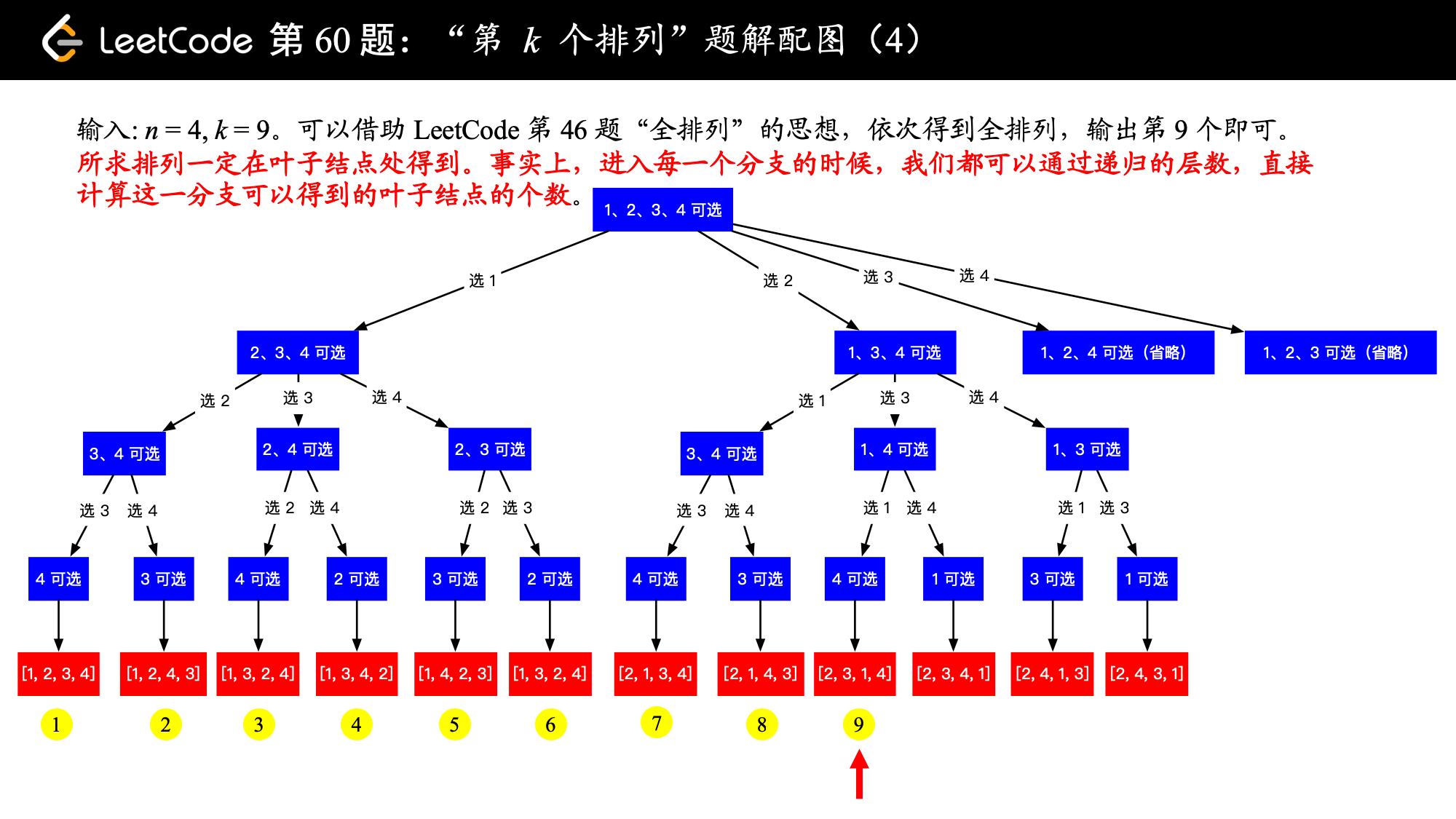
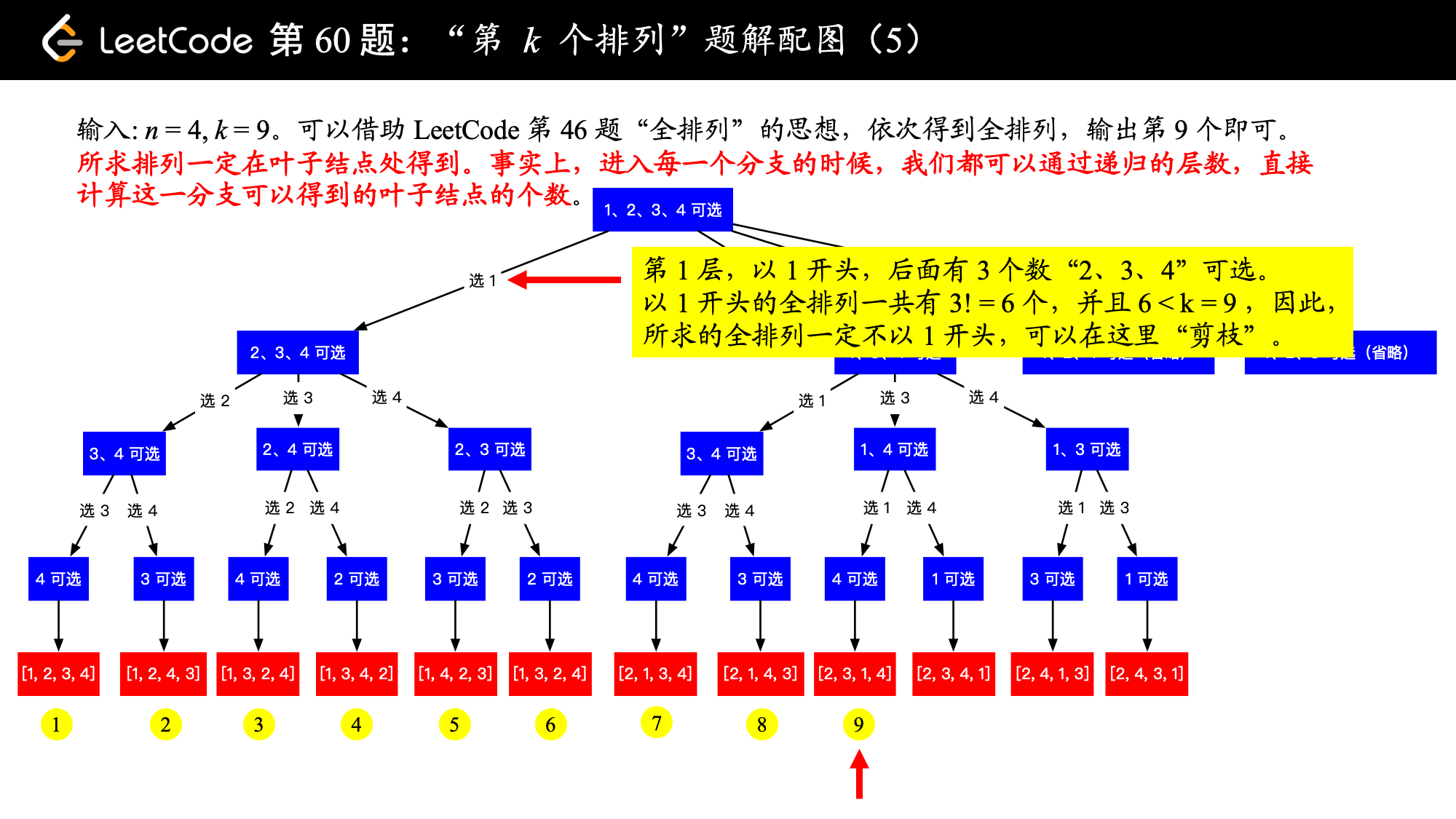
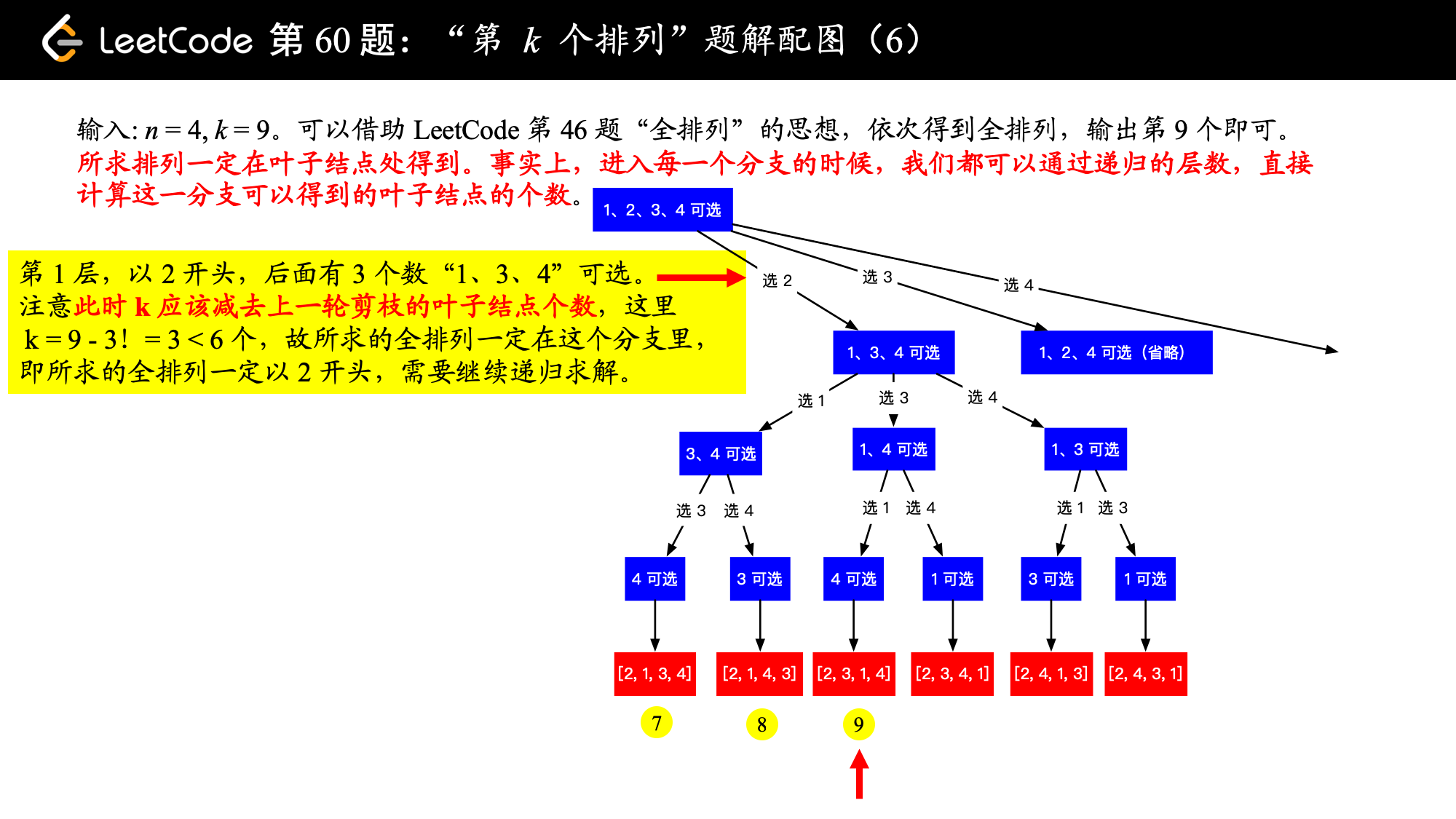
在编码上，我使用了「力扣」第 46 题：全排列的题解《回溯算法 + 位掩码（Python 代码、Java 代码）》的编码风格，如果阅读下面的代码有障碍的朋友，可以先看一看这篇题解，重点理解为什么要使用 used 数组。

参考代码 1：阶乘值通过计算得到。

Python 代码：

class Solution:

    def getPermutation(self, n: int, k: int) -> str:
        if n == 0:
            return []
        nums = [i + 1 for i in range(n)]
        used = [False for _ in range(n)]

        return self.__dfs(nums, used, n, k, 0, [])

    def __factorial(self, n):
        # 这种编码方式包括了 0 的阶乘是 1 这种情况
        res = 1
        while n:
            res *= n
            n -= 1
        return res

    def __dfs(self, nums, used, n, k, depth, pre):
        if depth == n:
            # 在叶子结点处结算
            return ''.join(pre)
        # 后面的数的全排列的个数
        ps = self.__factorial(n - 1 - depth)
        print(ps)
        for i in range(n):
            # 如果这个数用过，就不再考虑
            if used[i]:
                continue
            # 后面的数的全排列的个数小于 k 的时候，执行剪枝操作
            if ps < k:
                k -= ps
                continue
            pre.append(str(nums[i]))
            # 因为直接走到叶子结点，因此状态不用恢复
            used[i] = True
            return self.__dfs(nums, used, n, k, depth + 1, pre)

Java 代码：

import java.util.ArrayList;
import java.util.List;

public class Solution {

    public String getPermutation(int n, int k) {
        int[] nums = new int[n];
        boolean[] used = new boolean[n];
        for (int i = 0; i < n; i++) {
            nums[i] = i + 1;
            used[i] = false;
        }
        List<String> pre = new ArrayList<>();
        return dfs(nums, used, n, k, 0, pre);
    }

    private int factorial(int n) {
        // 这种编码方式包括了 0 的阶乘是 1 这种情况
        int res = 1;
        while (n > 0) {
            res *= n;
            n -= 1;
        }
        return res;
    }

    private String dfs(int[] nums, boolean[] used, int n, int k, int depth, List<String> pre) {
        if (depth == n) {
            StringBuilder sb = new StringBuilder();
            for (String c : pre) {
                sb.append(c);
            }
            return sb.toString();
        }
        int ps = factorial(n - 1 - depth);
        for (int i = 0; i < n; i++) {
            if (used[i]) {
                continue;
            }
            if (ps < k) {
                k -= ps;
                continue;
            }
            pre.add(nums[i] + "");
            used[i] = true;
            return dfs(nums, used, n, k, depth + 1, pre);
        }
        // 如果参数正确的话，代码不会走到这里
        throw new RuntimeException("参数错误");
    }
}

参考代码 2：阶乘值直接查表得到。

Python 代码：

class Solution:

    def getPermutation(self, n: int, k: int) -> str:
        if n == 0:
            return []
        nums = [i + 1 for i in range(n)]
        used = [False for _ in range(n)]
        factorial = [1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
        return self.__dfs(nums, used, n, k, 0, [], factorial)

    def __dfs(self, nums, used, n, k, depth, pre, factorial):
        if depth == n:
            # 在叶子结点处结算
            return ''.join(pre)
        # 后面的数的全排列的个数
        ps = factorial[n - 1 - depth]
        for i in range(n):
            # 如果这个数用过，就不再考虑
            if used[i]:
                continue
            # 后面的数的全排列的个数小于 k 的时候，执行剪枝操作
            if ps < k:
                k -= ps
                continue
            pre.append(str(nums[i]))
            # 因为直接走到叶子结点，因此状态不用恢复
            used[i] = True
            return self.__dfs(nums, used, n, k, depth + 1, pre, factorial)

Java 代码：

import java.util.ArrayList;
import java.util.List;

public class Solution {

    public String getPermutation(int n, int k) {
        int[] nums = new int[n];
        boolean[] used = new boolean[n];
        for (int i = 0; i < n; i++) {
            nums[i] = i + 1;
            used[i] = false;
        }
        int[] factorial = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};
        List<String> pre = new ArrayList<>();
        return dfs(nums, used, n, k, 0, pre, factorial);
    }

    private String dfs(int[] nums, boolean[] used, int n, int k, int depth, List<String> pre, int[] factorial) {
        if (depth == n) {
            StringBuilder sb = new StringBuilder();
            for (String c : pre) {
                sb.append(c);
            }
            return sb.toString();
        }
        int ps = factorial[n - 1 - depth];
        for (int i = 0; i < n; i++) {
            if (used[i]) {
                continue;
            }
            if (ps < k) {
                k -= ps;
                continue;
            }
            pre.add(nums[i] + "");
            used[i] = true;
            return dfs(nums, used, n, k, depth + 1, pre, factorial);
        }
        // 如果参数正确的话，代码不会走到这里
        throw new RuntimeException("参数错误");
    }
}

复杂度分析：

时间复杂度： $O(2^{N})$ ，回溯算法的时间复杂度是指数级别的，因为我们使用了大量的剪枝操作，故对于解这道问题是可以接受的。
空间复杂度： $O(N)$ ，nums、used、pre 都与 $N$ 等长，factorial 数组就 $10$ 个数，是常数级别的。

← LeetCode 第 47 题：“全排列 II”题解 LeetCode 第 77 题：“组合”题解 →

# LeetCode 第 60 题：“第 k 个排列”题解

# 回溯 + 剪枝（Python 代码、Java 代码）

LeetCode 第 60 题：“第 k 个排列”题解

回溯 + 剪枝（Python 代码、Java 代码）