LeetCode 第 1081 题：“不同字符的最小子序列”题解

说明：文本首发在力扣的题解版块，更新也会在第 1 时间在上面的网站中更新，这篇文章只是上面的文章的一个快照，您可以点击上面的链接看到其他网友对本文的评论。

返回字符串 text 中按字典序排列最小的子序列，该子序列包含 text 中所有不同字符一次。

示例 1：

输入："cdadabcc" 输出："adbc" 示例 2：

输入："abcd" 输出："abcd" 示例 3：

输入："ecbacba" 输出："eacb" 示例 4：

输入："leetcode" 输出："letcod"

提示：

1 <= text.length <= 1000 text 由小写英文字母组成

贪心算法 + 栈、位掩码（Python 代码、Java 代码）

理解题意

首先理解题意。

1、字典序

建议在网上搜索关键字“字典序”，我这里通过例子解释“字典序”的概念。如果一个字符串含有 1 个字母 a、2 个字母 b、和 1 个字母 c。那么这个字符串可以是 aabc，也可以是 abac，也可以是 aacb，它们的字典序为：

aabc < aacb < abac

即从第 0 位开始比较，ascii 码数值小的排在前面，如果遇到相同字母，就延后一位比较 ascii 码数值大小。

2、子序列

要注意这里子序列的含义：
（1）并不要求是连续子序列，例如 aabc 的子序列之一可以是 ac；
（2）子序列中各个字符的相对顺序应该与原字符串一致，例如 ca 就不是 aabc 的子序列；
（3）子序列包含 text 中所有不同字符一次，这里注意关键词 “所有” 和 “一次”，所以要求我们找出的子序列包含的字符应该是 “不重不漏” 的。

思路分析

根据题目，这是一个“最优化问题”，根据字典序的定义比较容易想到的是，我们尽量让字典序靠前的字符出现在子序列的前面，如果子序列中每个字符的 ascii 码数值是依次增加的，那无疑是这个子序列就是所有子序列中字典序最靠前的那个子序列。

那如果那些字典序靠前的字符出现得比较晚该怎么办呢？此时就要看，已经出现过的字符将来还有没有可能出现，如果将来有可能出现，就把前面的字符依次删去，经过这样的流程，得到的子序列就符合题意，这是 贪心算法 的思想，局部最优则全局最优。

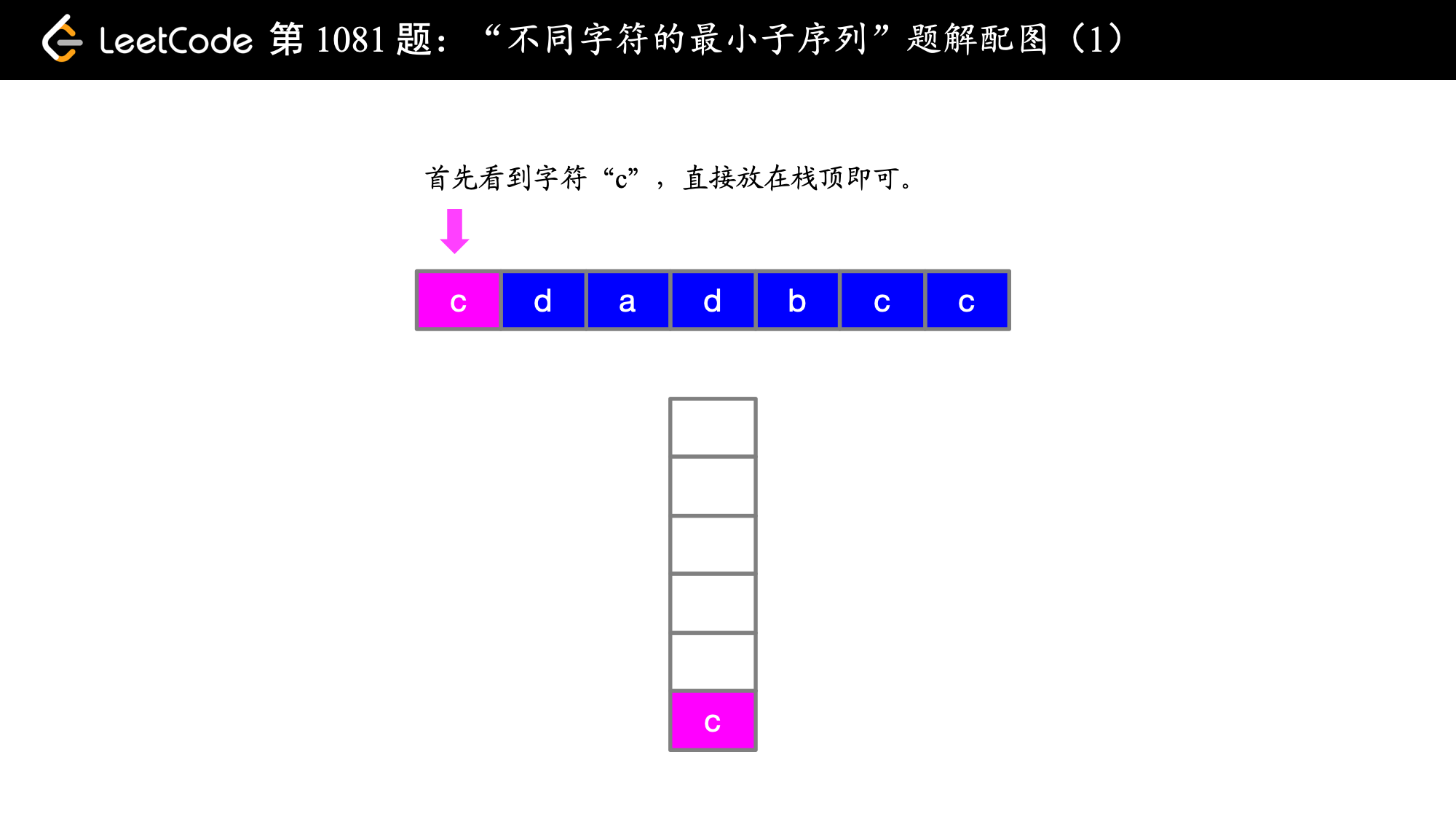
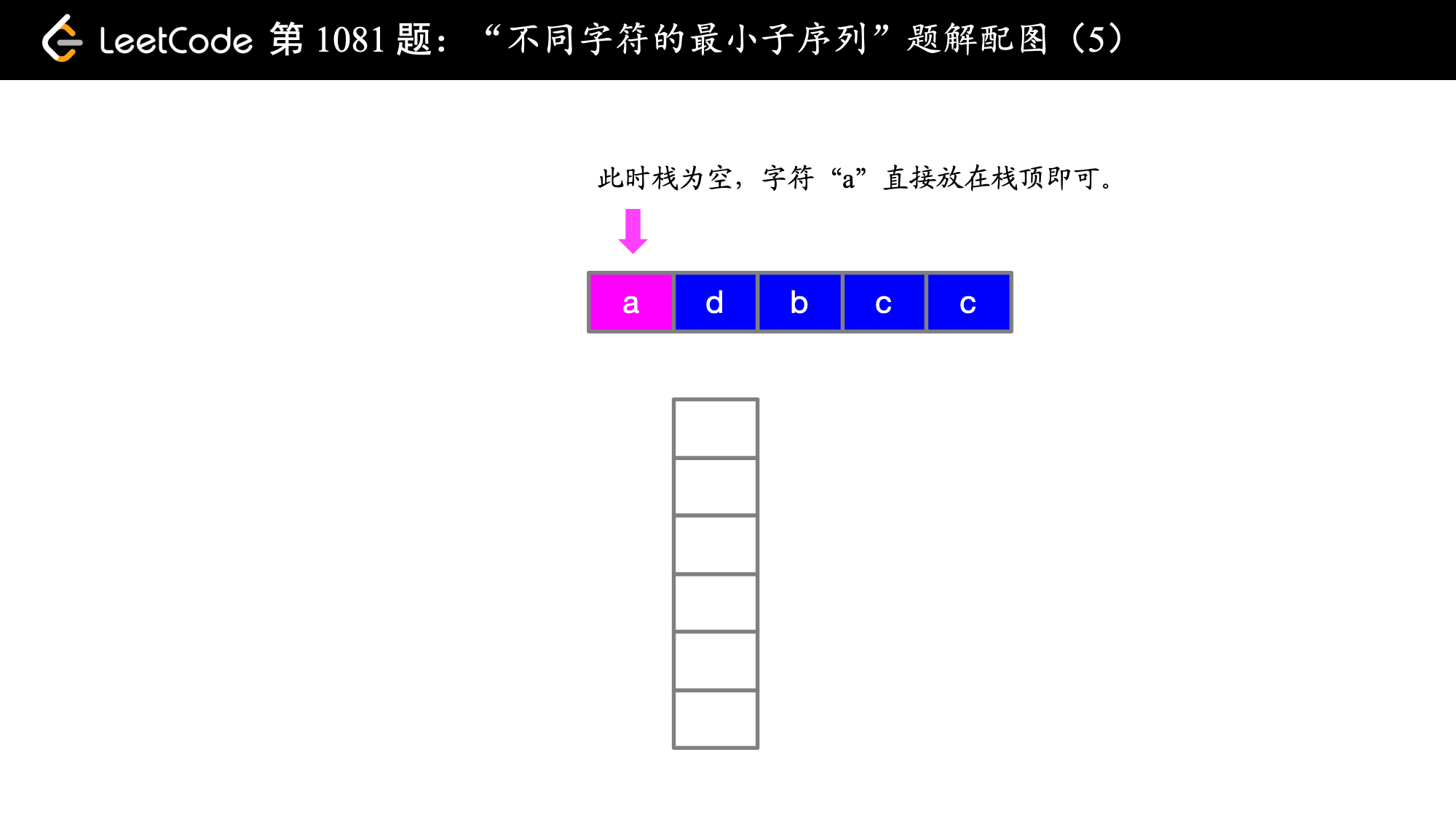
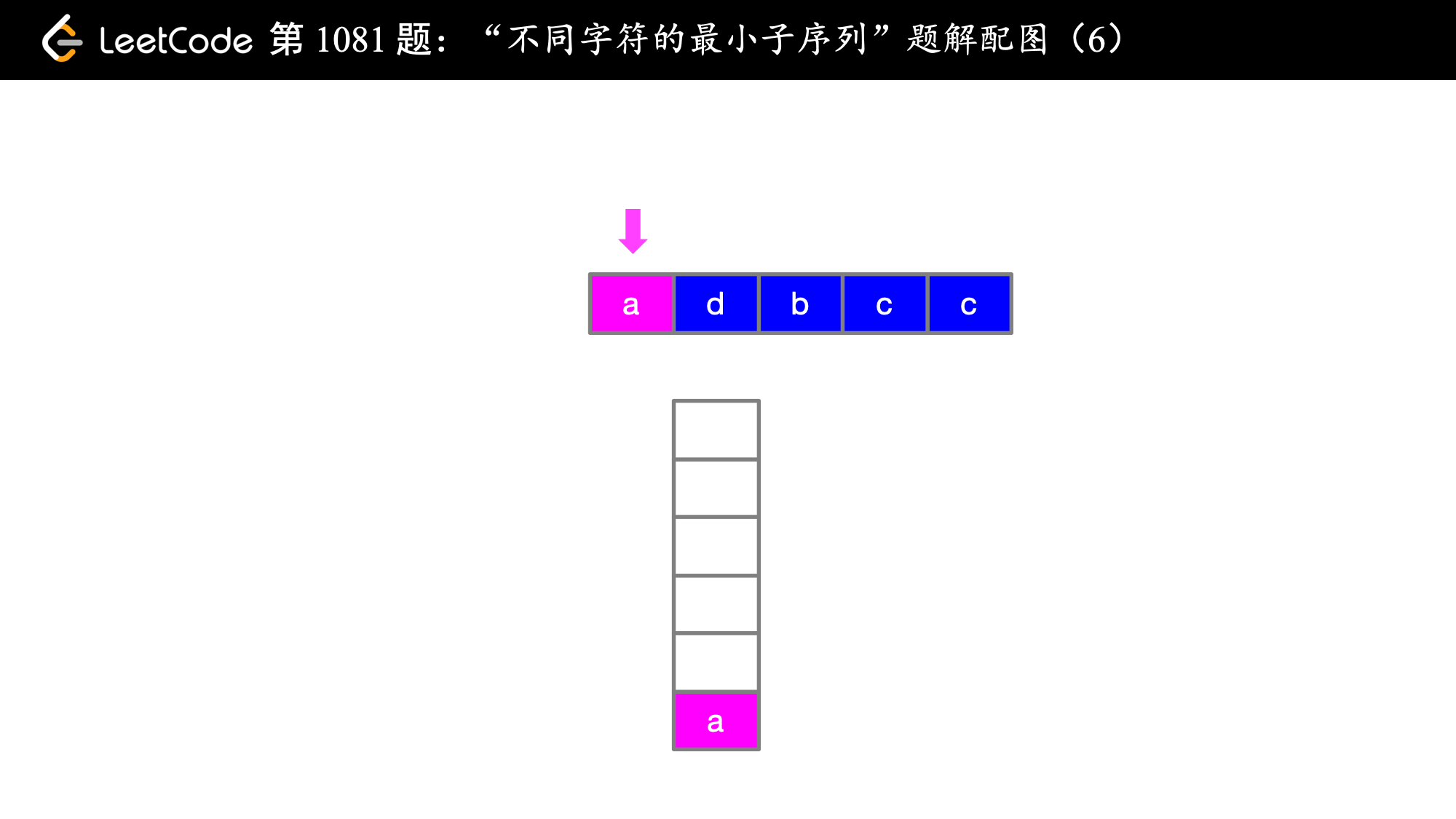
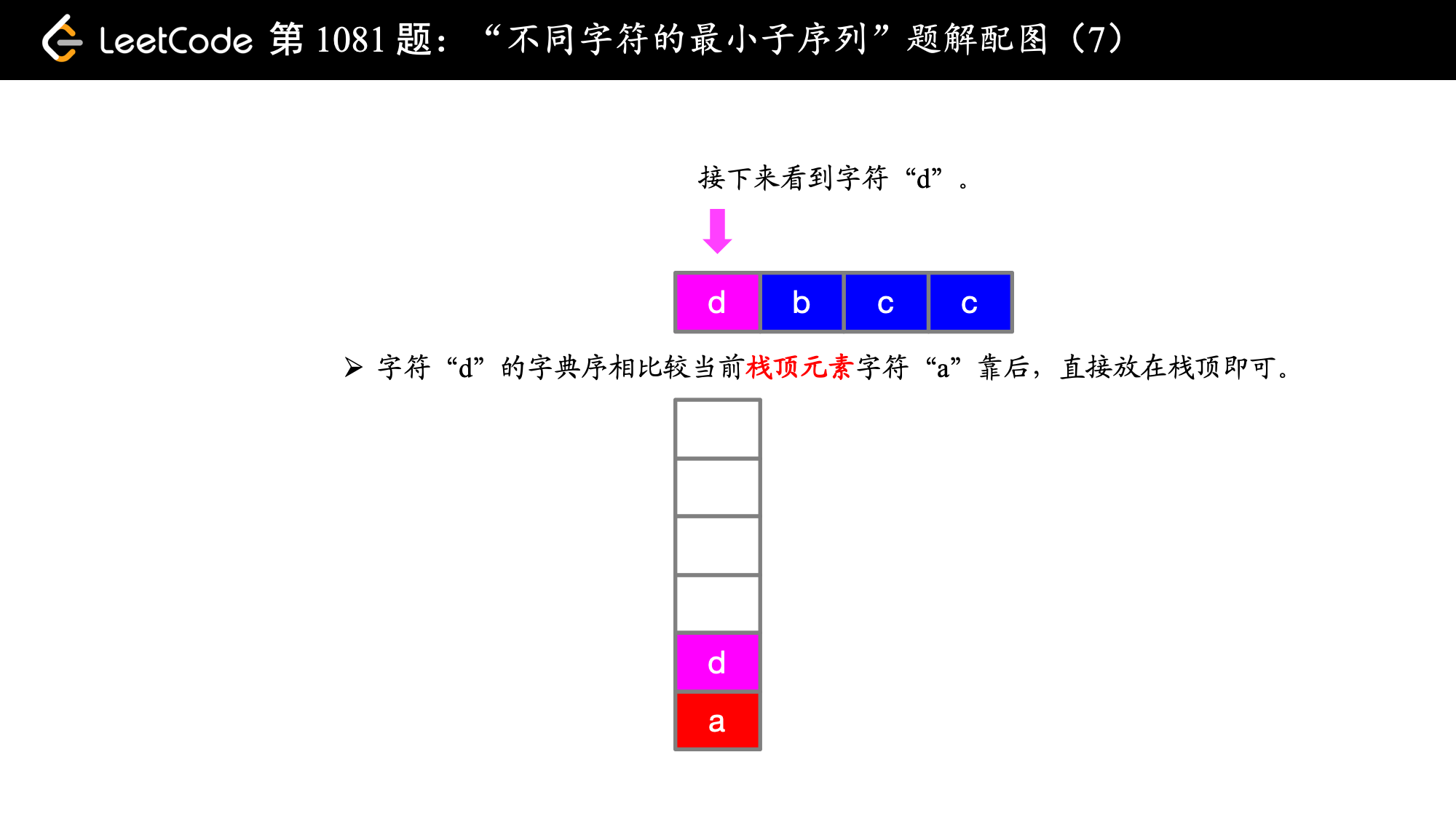
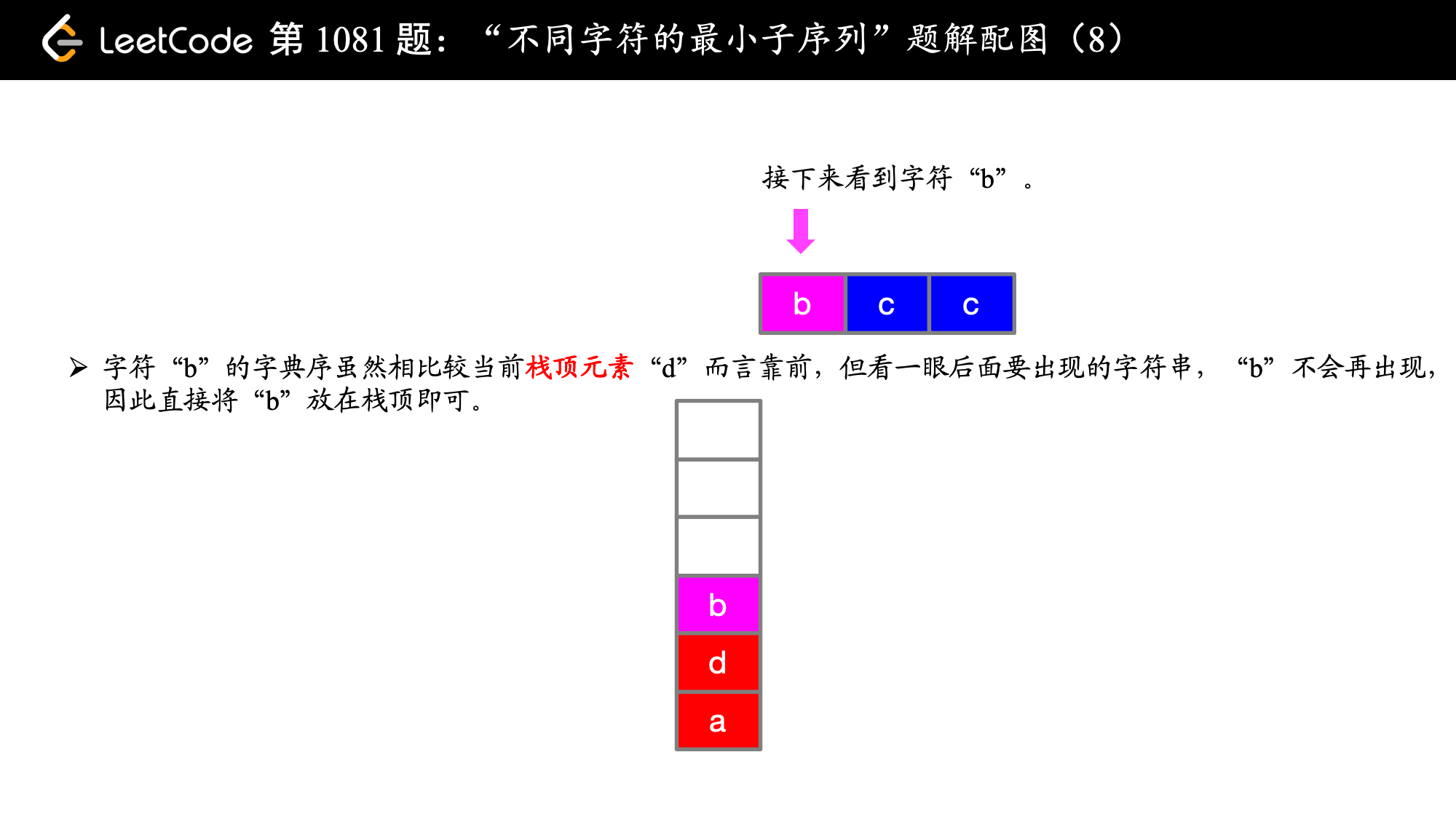
下面以例 1 cdadabcc 讲解一下算法的具体执行流程：

（温馨提示：下面的幻灯片中，有几页上有较多的文字，可能需要您停留一下，可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。）

,,,,,,,,,

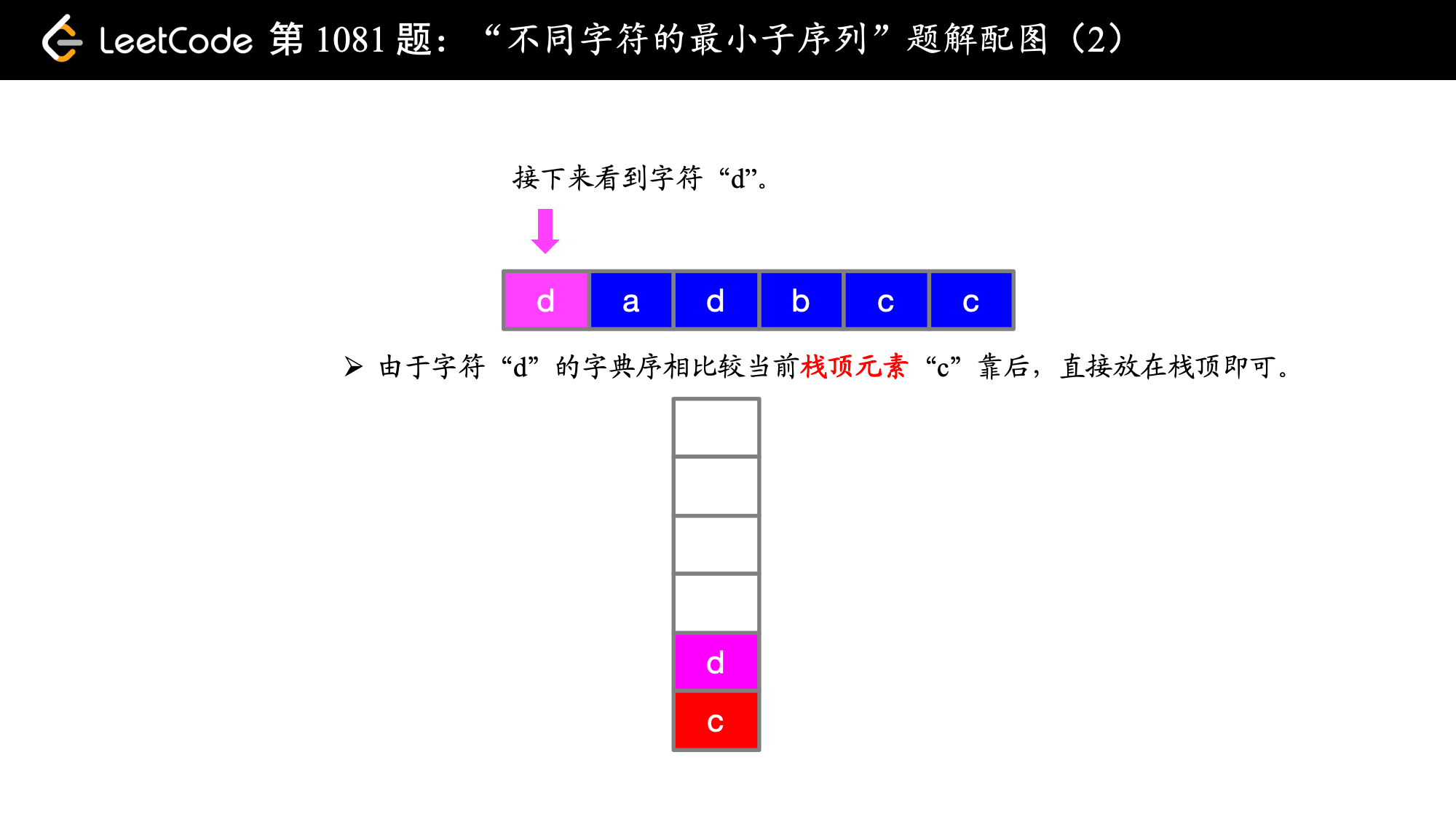
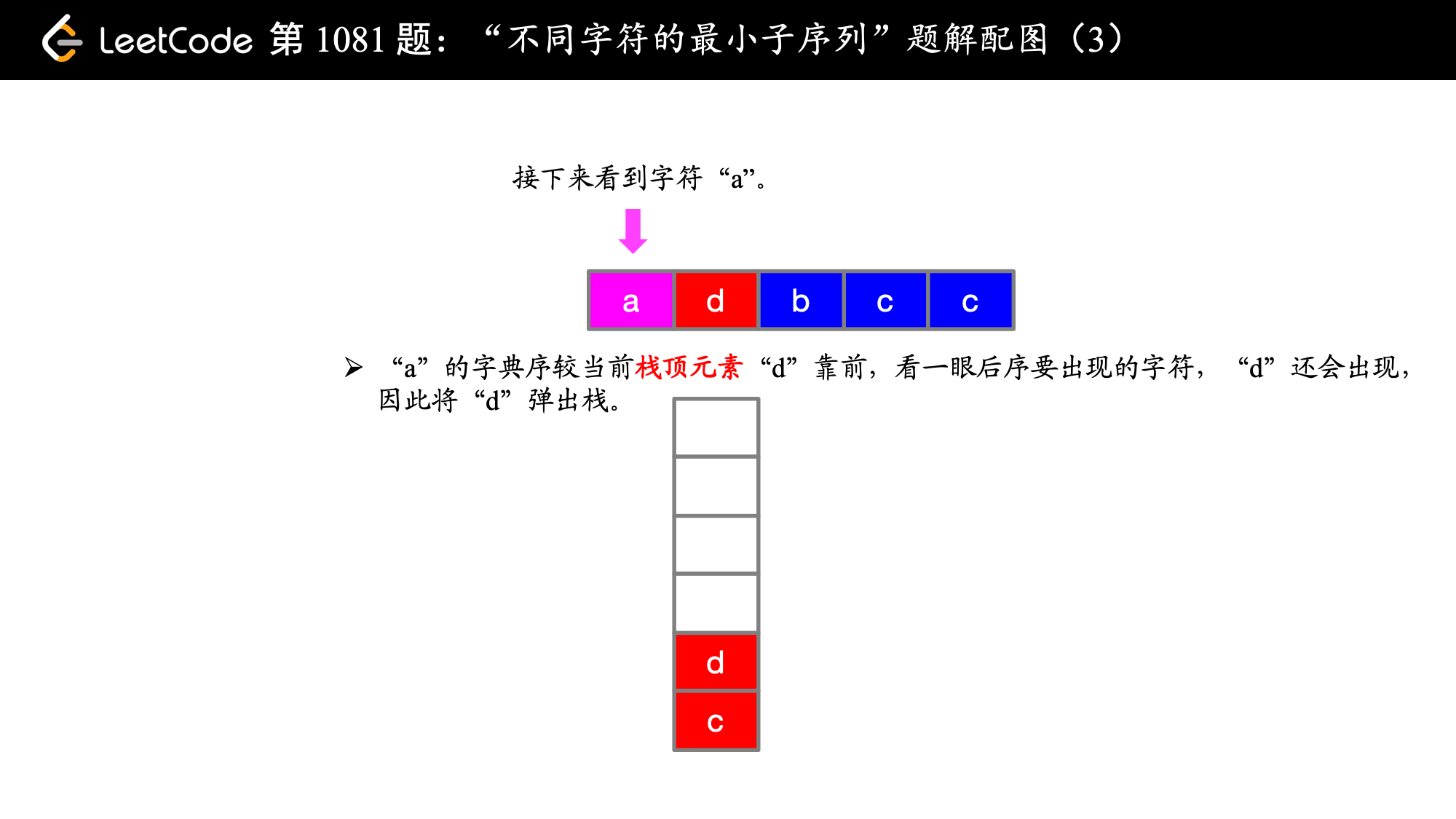
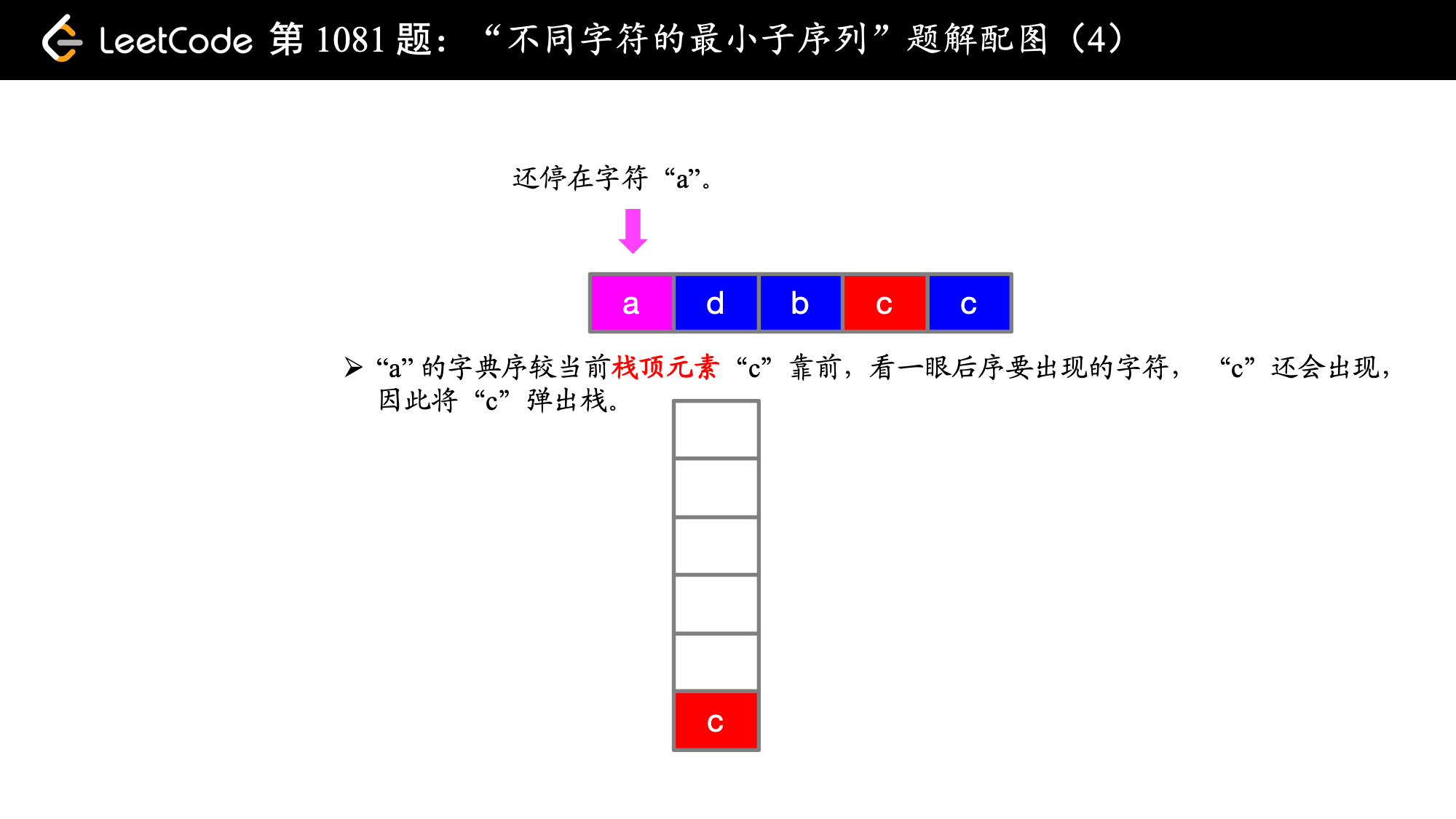
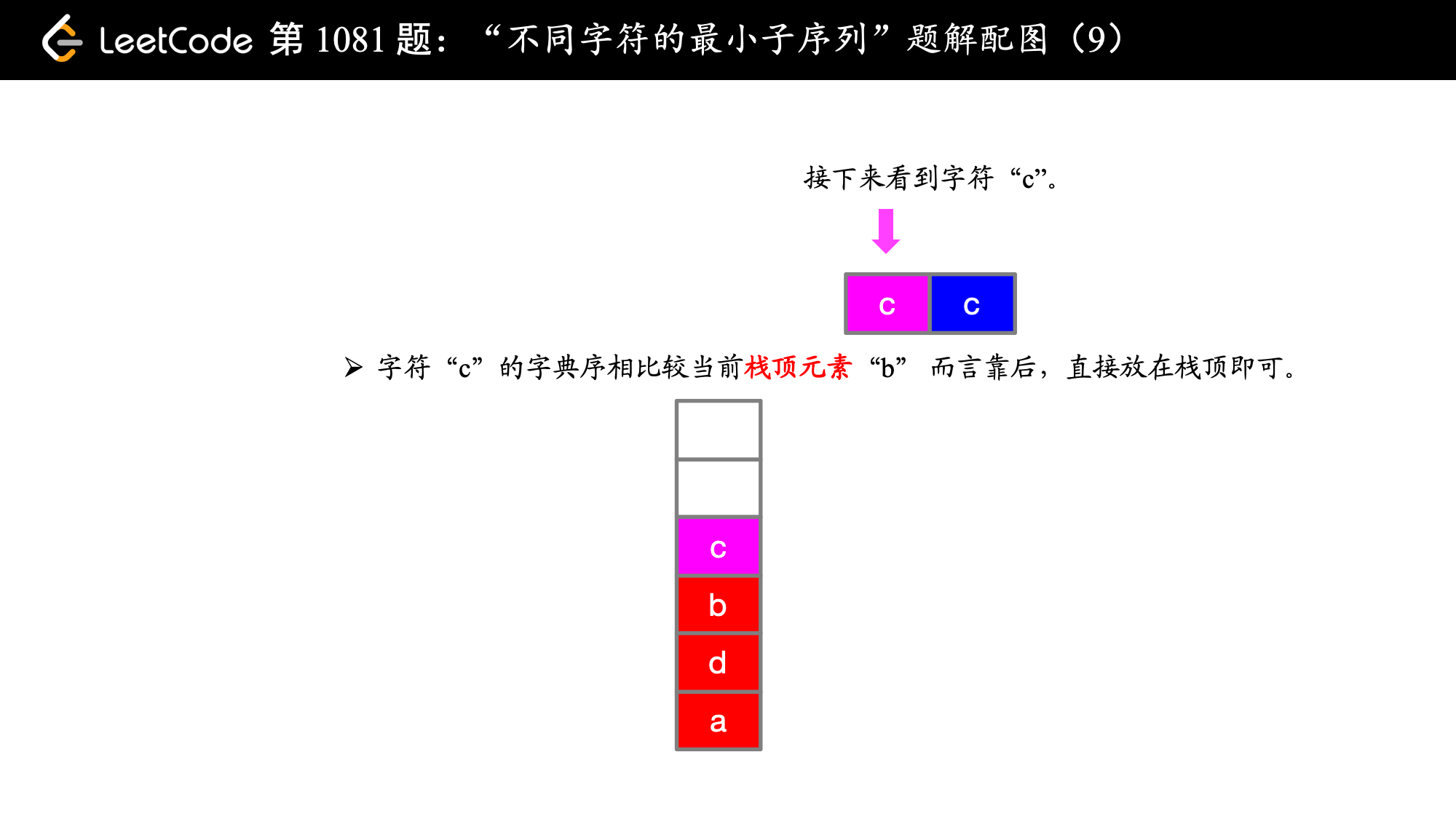
在第 1 步和第 2 步的时候，即在遍历索引为 0 和索引为 1 的字符的时候，字典序 c < d 成立，故 cd 是目前为止得到的字典序最靠前的子序列，这是显然的，关键是当 a 来了之后，此时 a 前面的 d 是字典序靠后的字符，此时想到有没有可能后面还有 d，看了一眼，果然有 d ，那就把前面的 d 放弃，用同样的方式考察 c，发现后面 c 还有可能出现，因此 c 也被放弃了，此时我们就让字典序最靠前的 a 在最终得到的子序列的最前面（局部最优体现在这里）。

到了第 5 步的时候，虽然 b 的字典序比它前面的 d 要靠前，但此时 d 不会再出现，因此 d 就不能离开当前子序列。

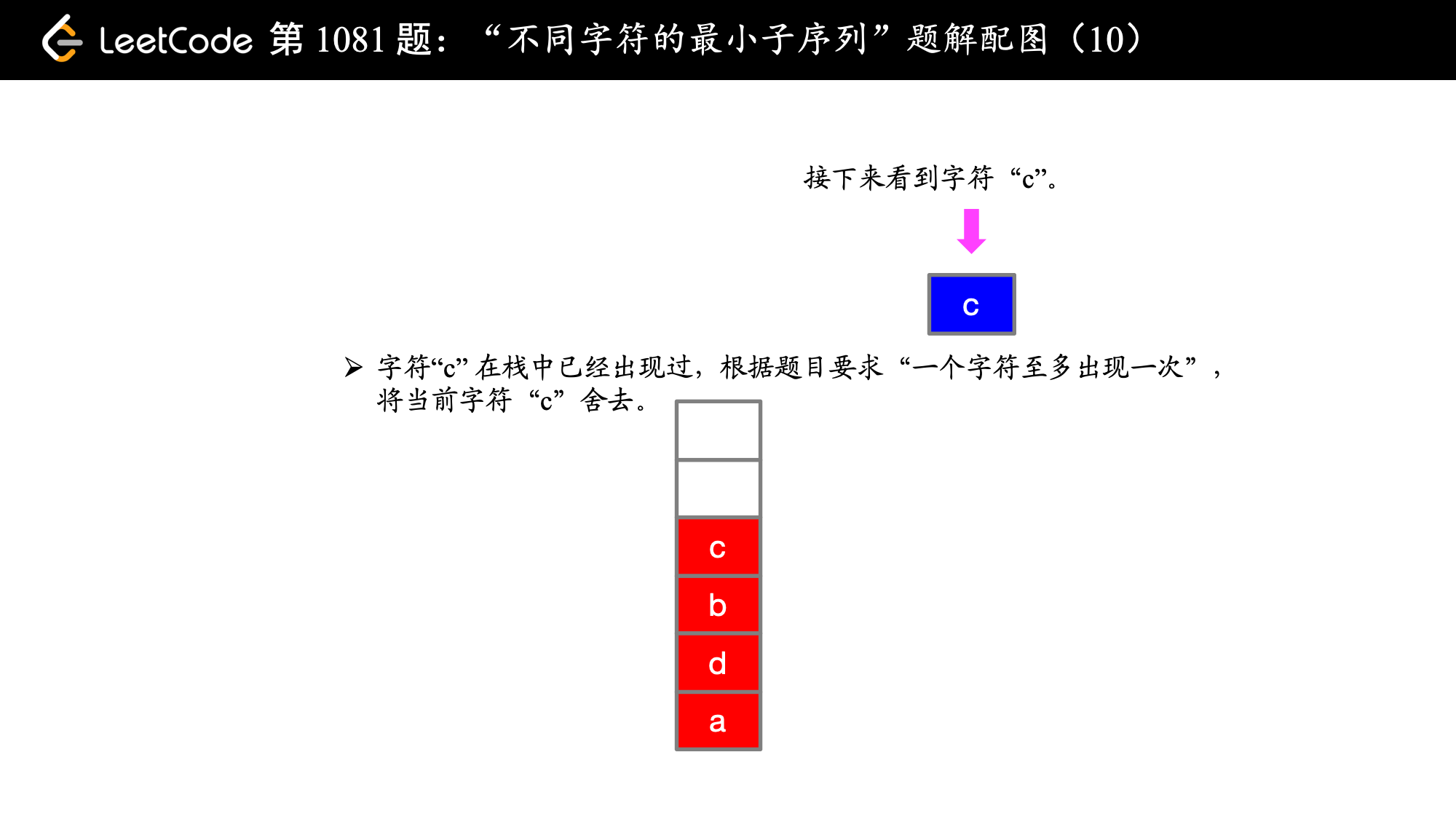
第 7 步，c 在之前的子序列中已经出现过了，就不再考虑。

编码实现

Python 代码：

class Solution:
    def smallestSubsequence(self, text: str) -> str:
        size = len(text)
        stack = []
        for i in range(size):
            if text[i] in stack:
                continue
            while stack and ord(text[i]) < ord(stack[-1]) and \
                    text.find(stack[-1], i) != -1:
                stack.pop()
            stack.append(text[i])
        return ''.join(stack)

Java 代码：

import java.util.Stack;

public class Solution {

    public String smallestSubsequence(String text) {
        int len = text.length();
        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < len; i++) {
            Character c = text.charAt(i);
            if (stack.contains(c)) {
                continue;
            }
            while (!stack.empty() && c < stack.peek() && text.indexOf(stack.peek(), i) != -1) {
                stack.pop();
            }
            stack.push(c);
        }
        StringBuilder sb = new StringBuilder();
        for (Character c : stack) {
            sb.append(c);
        }
        return sb.toString();
    }
}

解释：这里使用 text[i] in stack 看一个字符是不是已经出现过，使用 text.find(stack[-1], i) != -1 看栈顶的那个字符将来会不会出现。这里两个方法都用到了 Python 的库函数。

注意到，题目当中有说到 “text 由小写英文字母组成”，因此字母就一共只有 26 个，上面两个方法都是在判重，因此比较容易想到使用位掩码的技巧。

Python 代码：

class Solution:
    def smallestSubsequence(self, text: str) -> str:
        size = len(text)
        stack = []
        pre = 0
        # 从索引 i 到索引 size - 1 的位掩码
        post = [0] * size

        for i in range(size):
            for j in range(i, size):
                post[i] |= (1 << (ord(text[j]) - ord('a')))

        for i in range(size):
            # print(stack, text[i])
            if pre & (1 << ord(text[i]) - ord('a')):
                # print(i, pre & (1 << ord(text[i]) - ord('a')))
                continue
            while stack and ord(text[i]) < ord(stack[-1]) \
                    and post[i] & (1 << (ord(stack[-1]) - ord('a'))):
                top = stack.pop()
                pre ^= (1 << ord(top) - ord('a'))
            pre |= (1 << ord(text[i]) - ord('a'))
            stack.append(text[i])
        return ''.join(stack)

Java 代码：

import java.util.Stack;

public class Solution {

    public String smallestSubsequence(String text) {
        int len = text.length();
        // 从索引 i 到索引 size - 1 的位掩码
        int[] post = new int[len];
        int pre = 0;
        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < len; i++) {
            for (int j = i; j < len; j++) {
                // System.out.println(text.charAt(j));
                post[i] |= (1 << (text.charAt(j) - 'a'));
            }
        }

        // System.out.println(Arrays.toString(post));
        for (int i = 0; i < len; i++) {
            Character c = text.charAt(i);
            if ((pre & (1 << (c - 'a'))) > 0) {
                continue;
            }
            while (!stack.empty() && c < stack.peek() &&
                    (post[i] & (1 << (stack.peek() - 'a'))) != 0) {
                Character top = stack.pop();
                pre ^= (1 << top - 'a');
            }
            pre |= (1 << c - 'a');
            stack.push(c);
        }
        StringBuilder sb = new StringBuilder();
        for (Character c : stack) {
            sb.append(c);
        }
        return sb.toString();
    }
}

← LeetCode 第 455 题：“分发饼干”题解

# LeetCode 第 1081 题：“不同字符的最小子序列”题解

# 贪心算法 + 栈、位掩码（Python 代码、Java 代码）

# 理解题意

# 1、字典序

# 2、子序列

# 思路分析

# 编码实现