LeetCode 第 23 题：“合并 K 个排序链表”题解

题解地址：贪心算法、优先队列 + 分治法（Python 代码、Java 代码）。

说明：文本首发在力扣的题解版块，更新也会在第 1 时间在上面的网站中更新，这篇文章只是上面的文章的一个快照，您可以点击上面的链接看到其他网友对本文的评论。

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

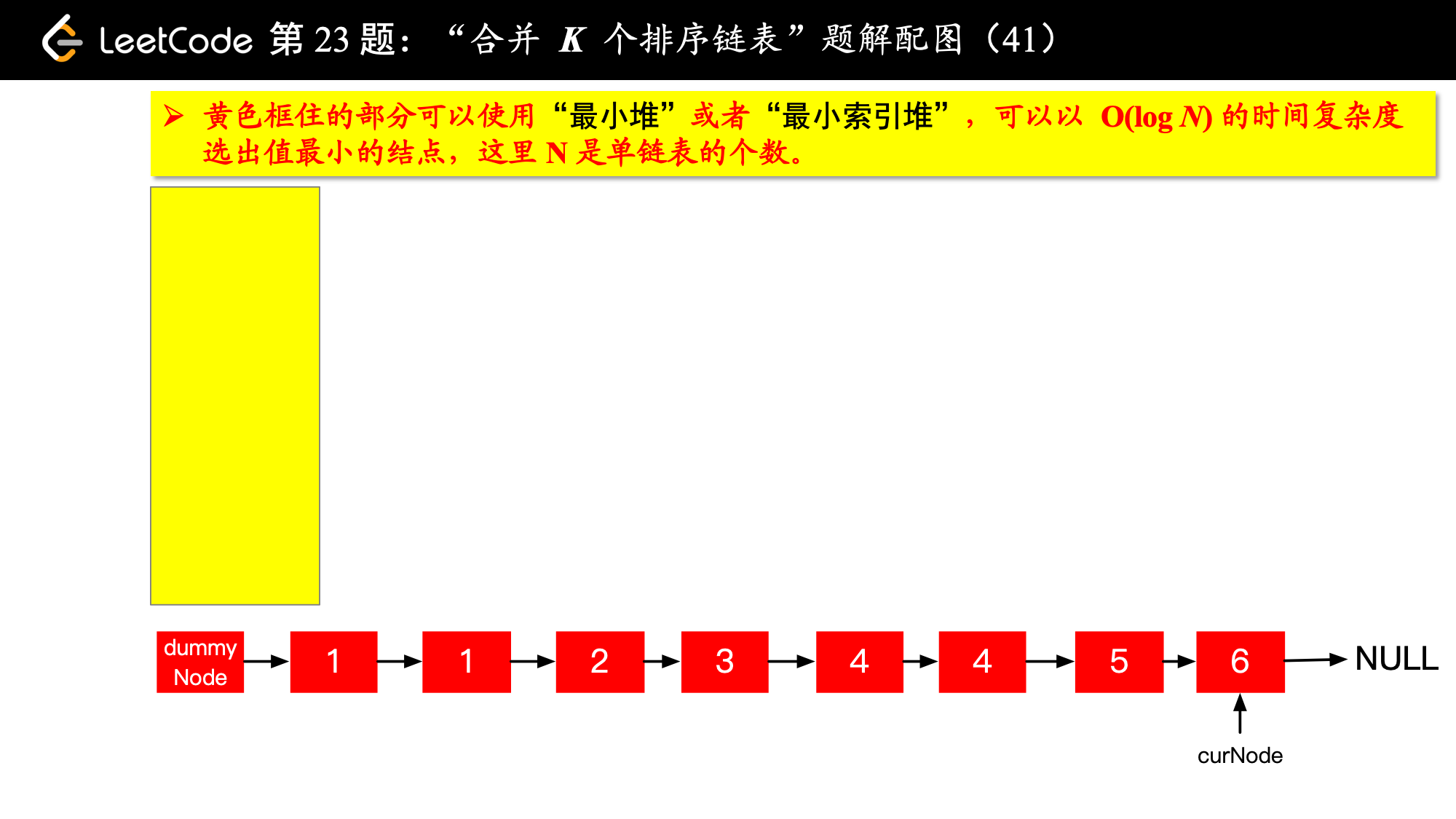
输入: [ 1->4->5, 1->3->4, 2->6 ] 输出: 1->1->2->3->4->4->5->6

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/merge-k-sorted-lists 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

贪心算法、优先队列 + 分治法（Python 代码、Java 代码）

方法一：贪心算法、优先队列

思路分析：

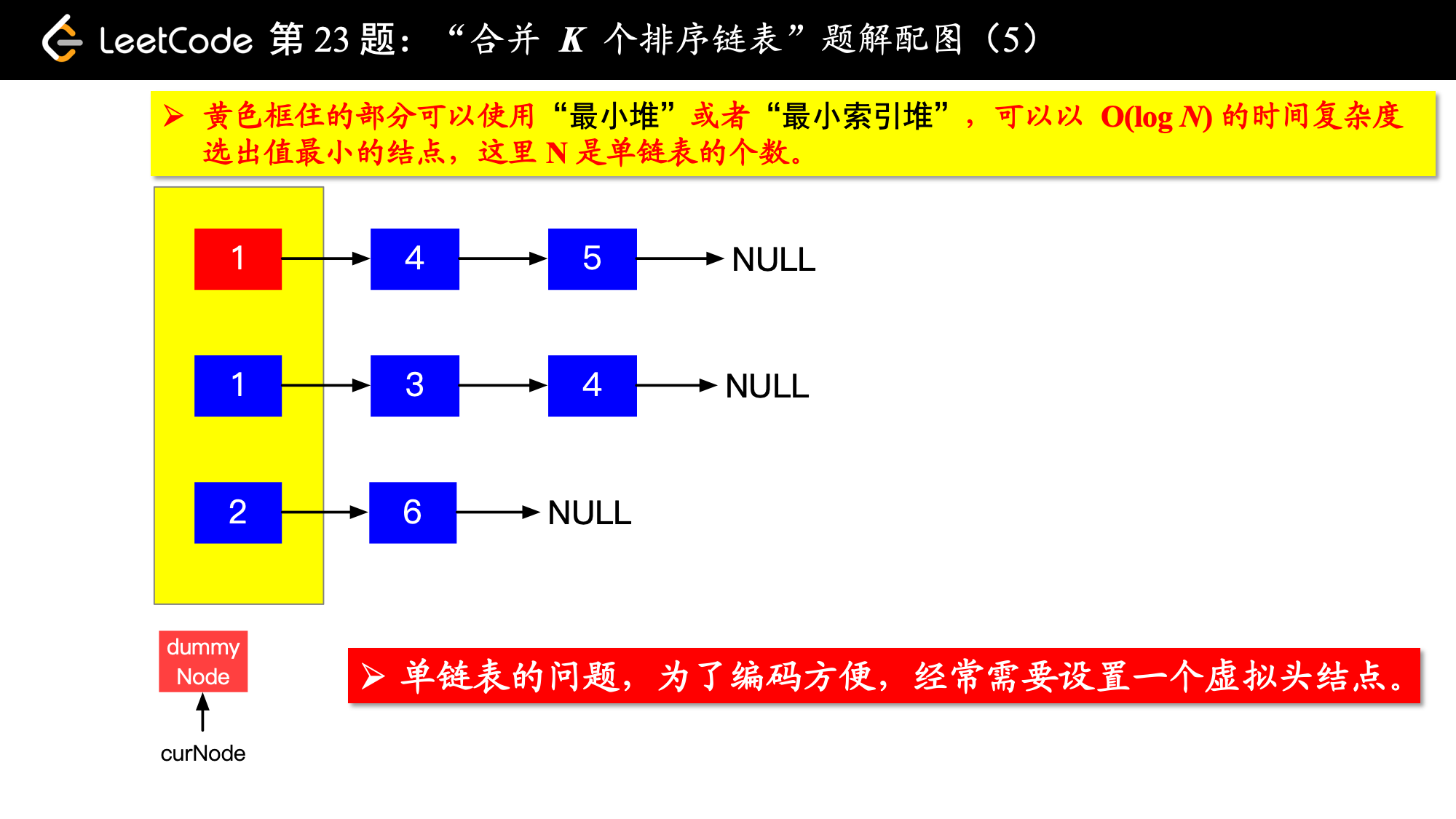
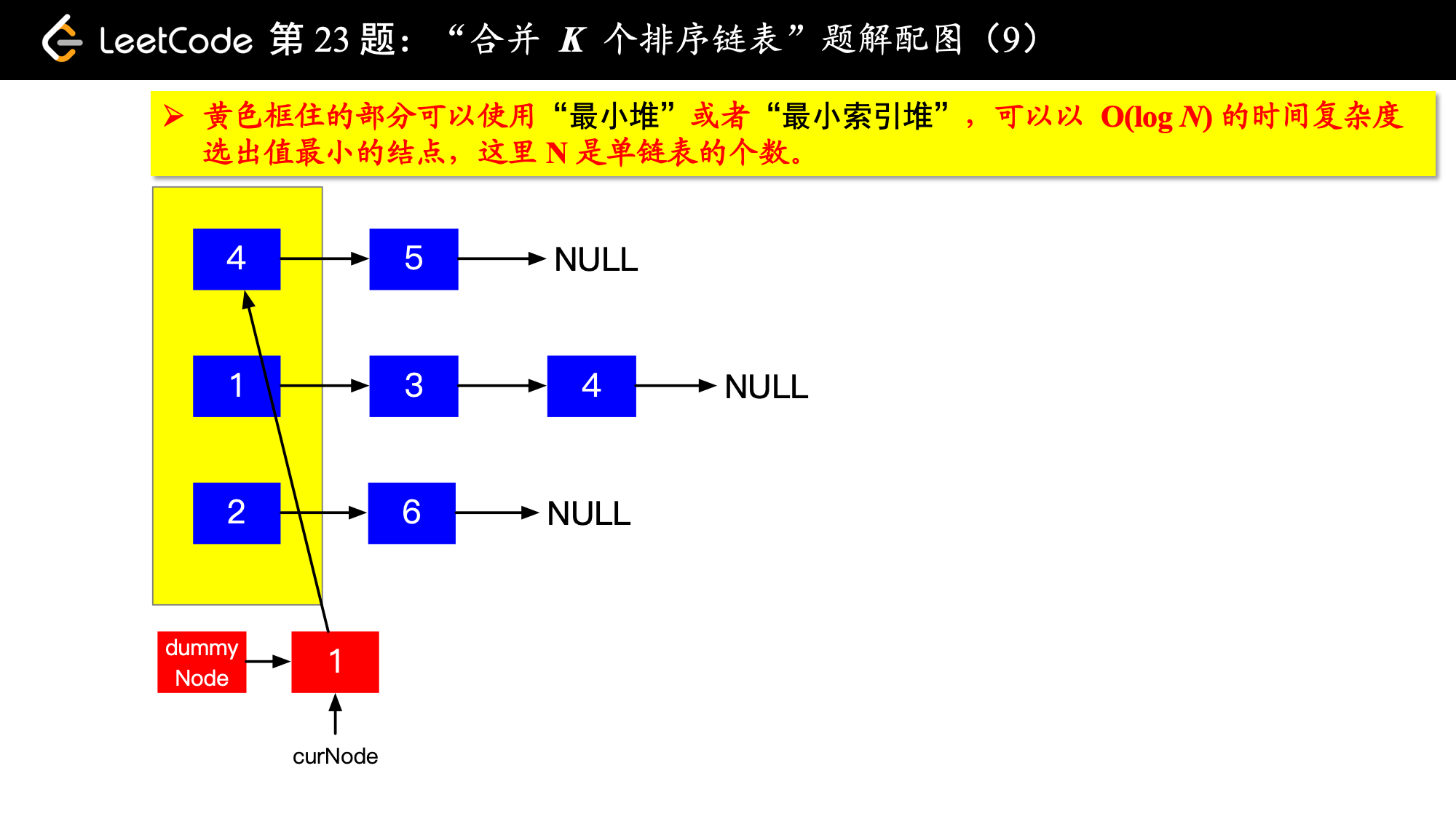
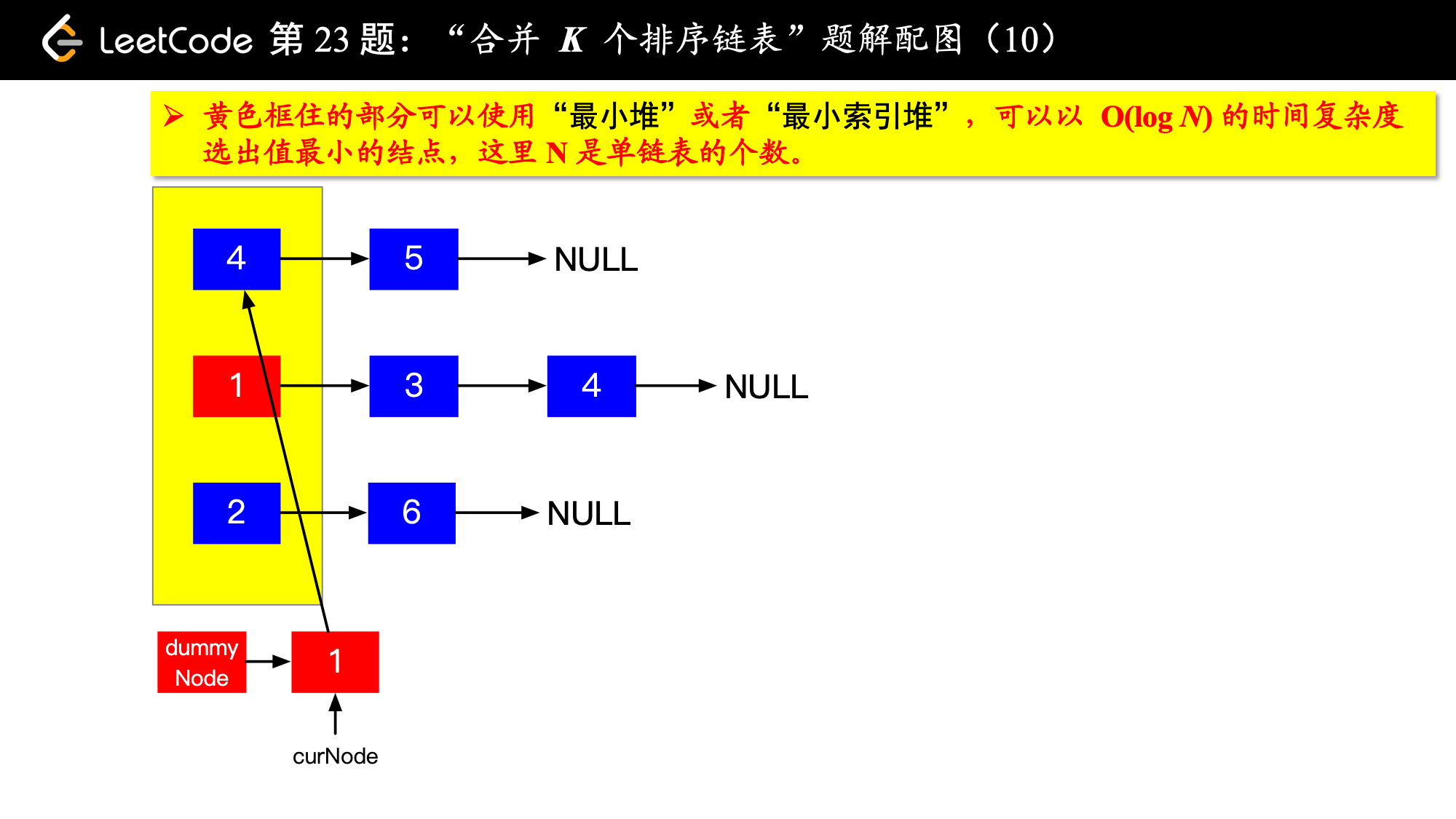
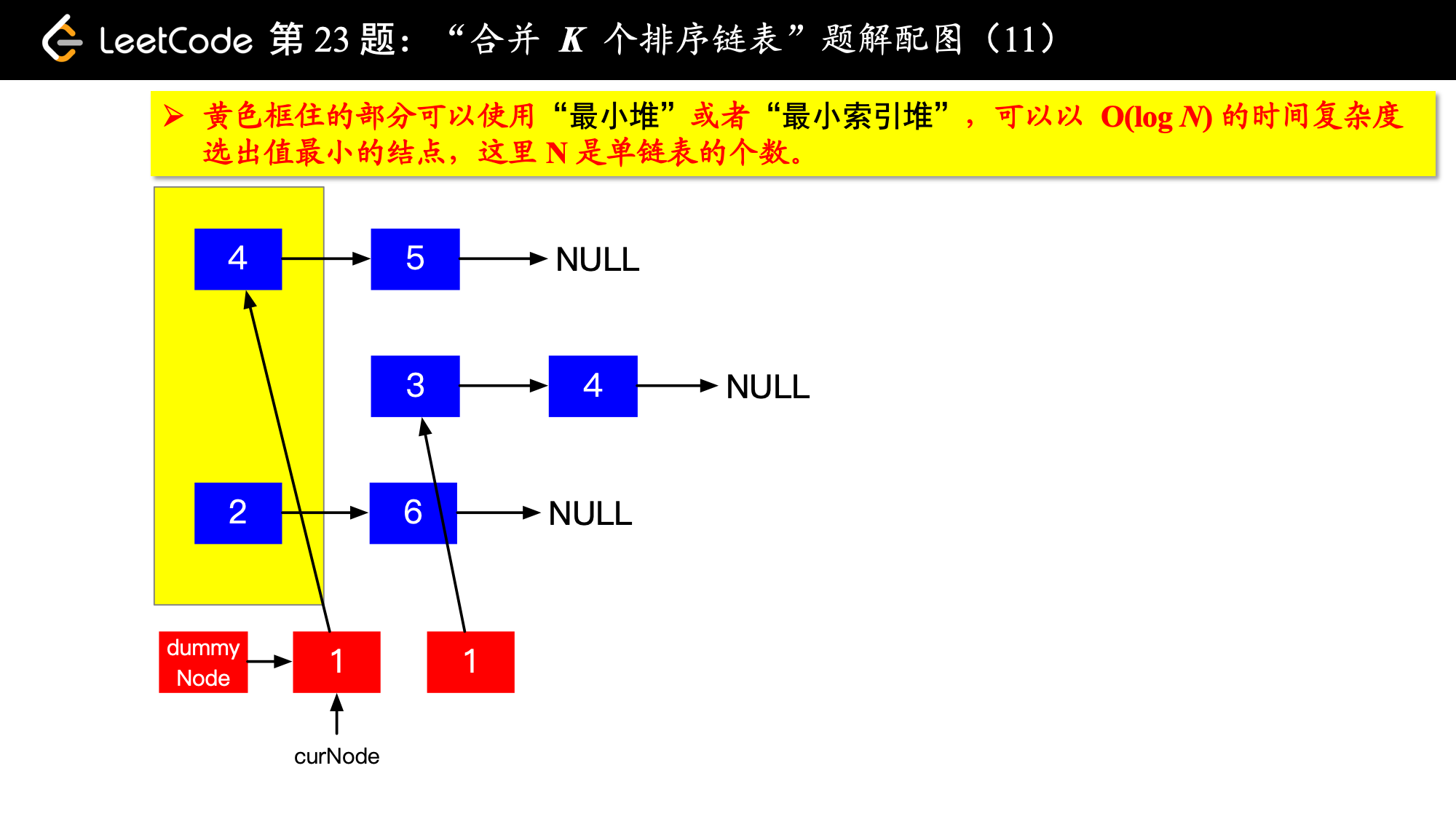
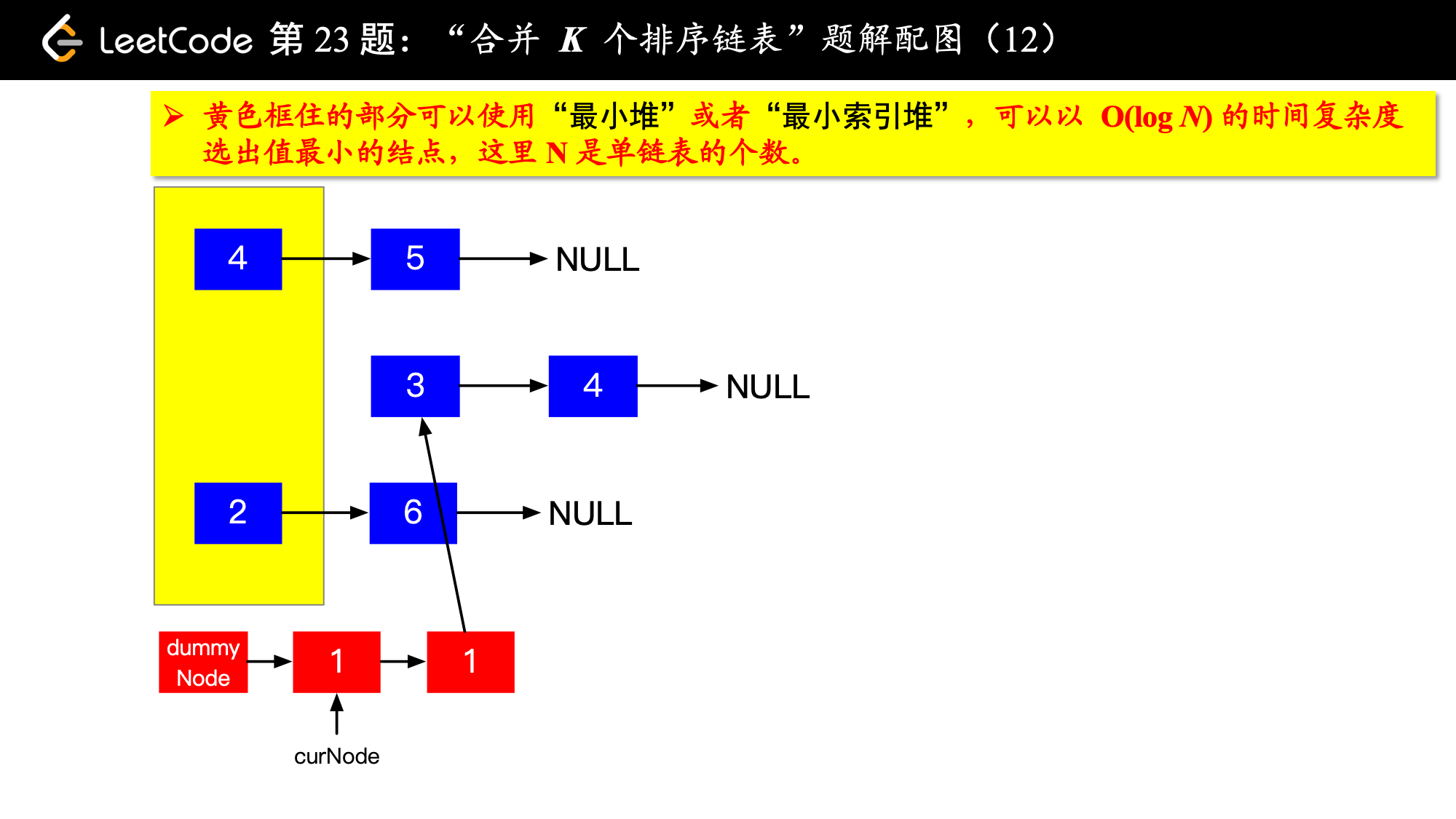
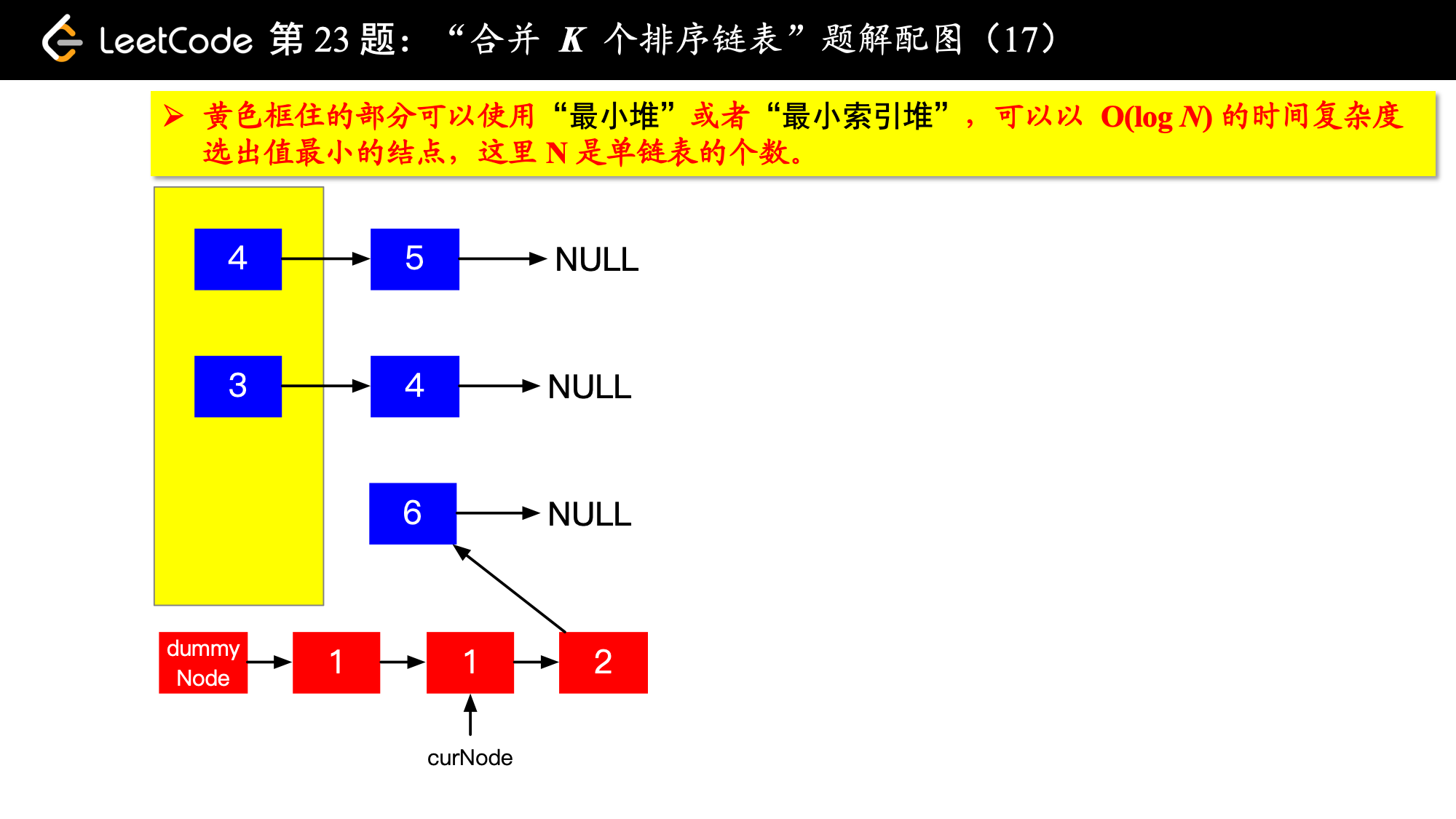
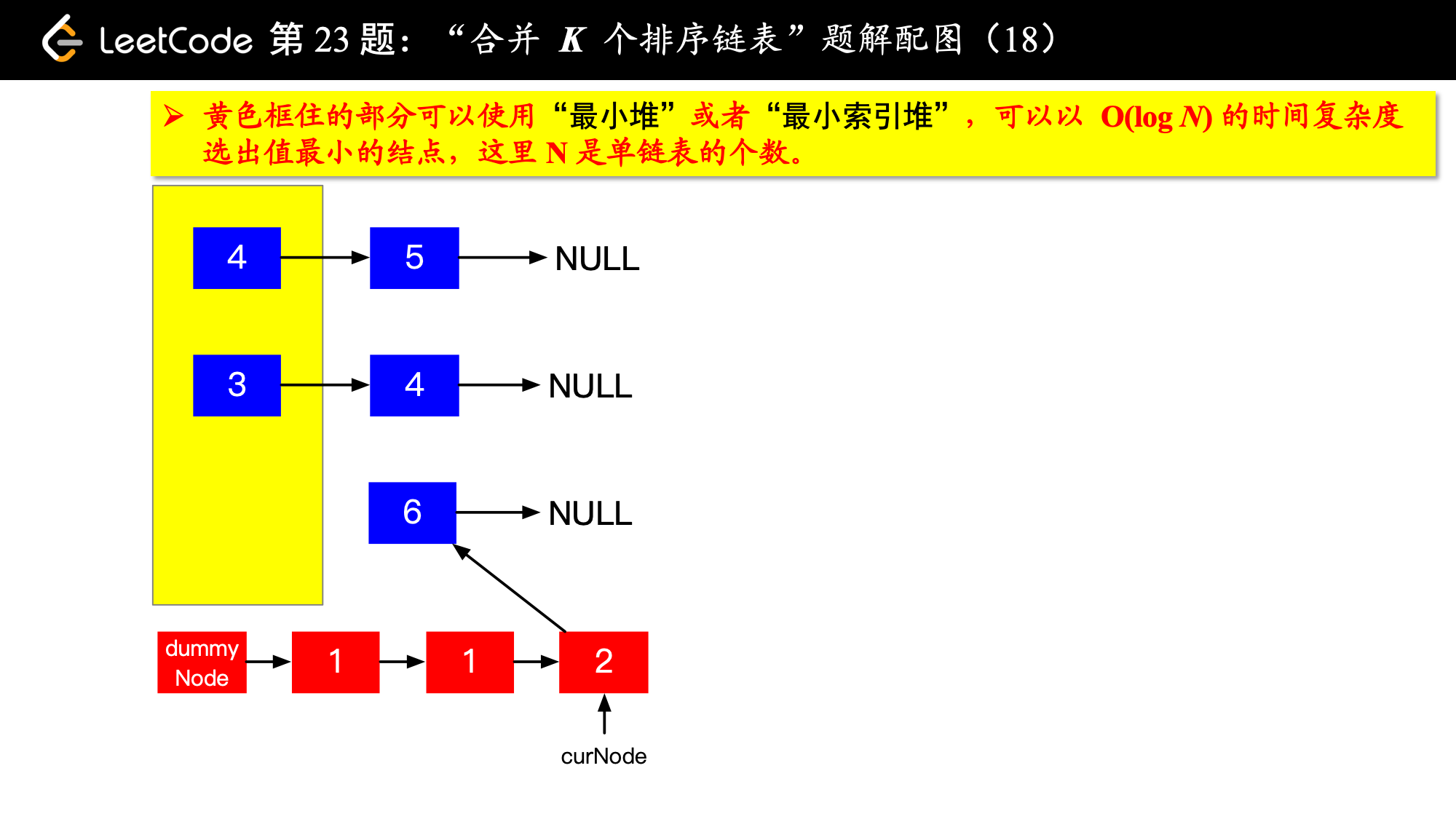
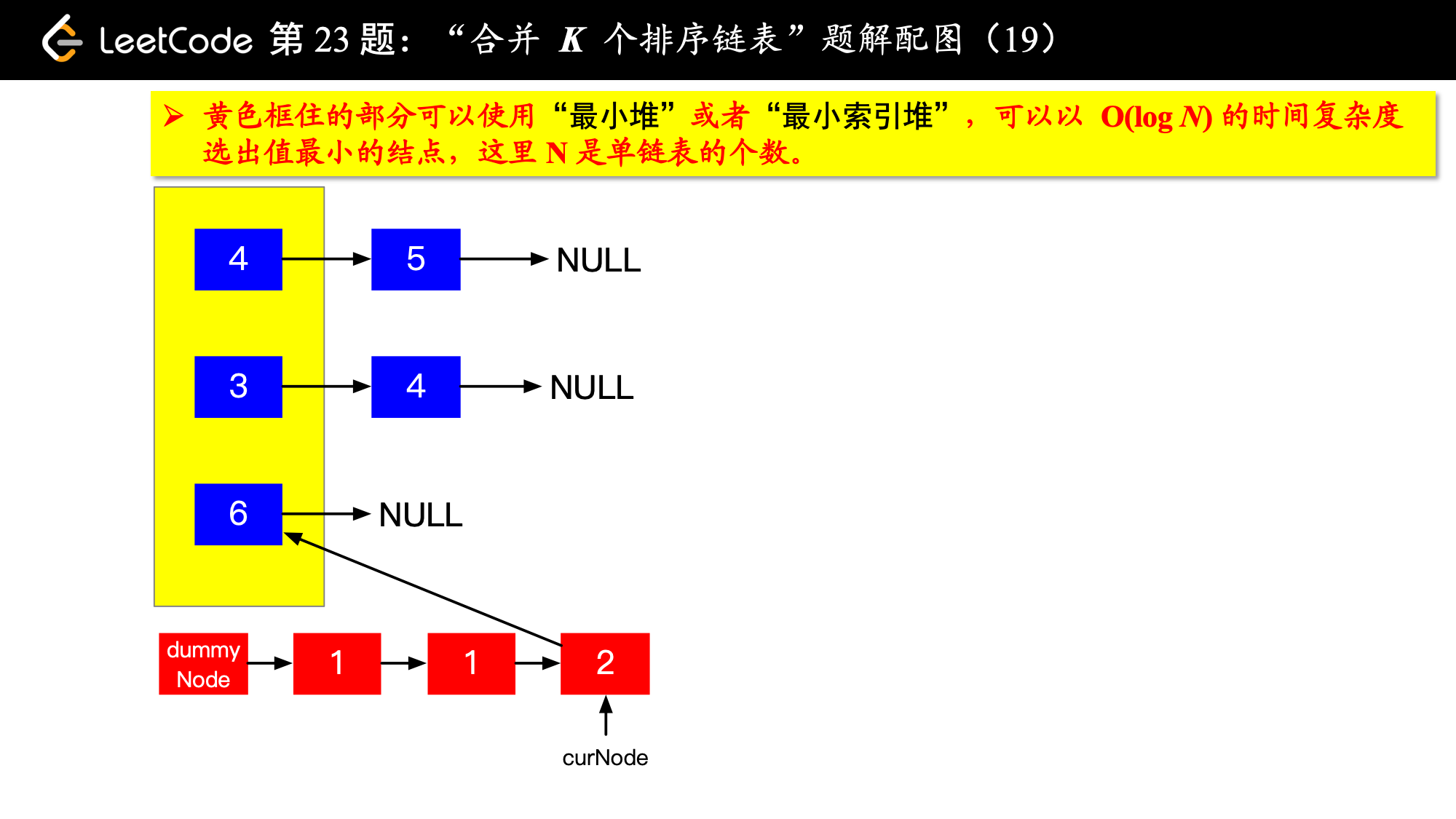
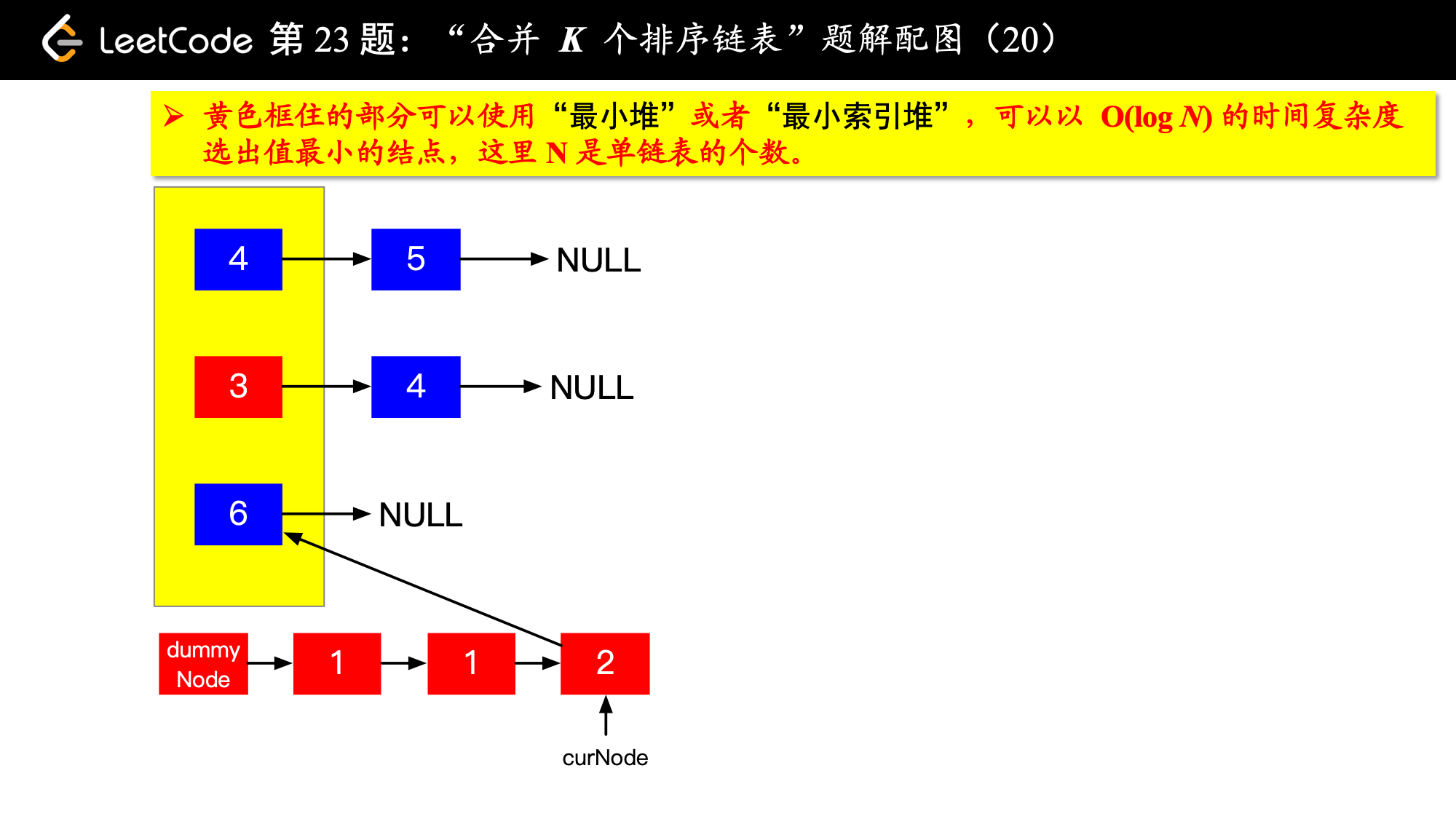
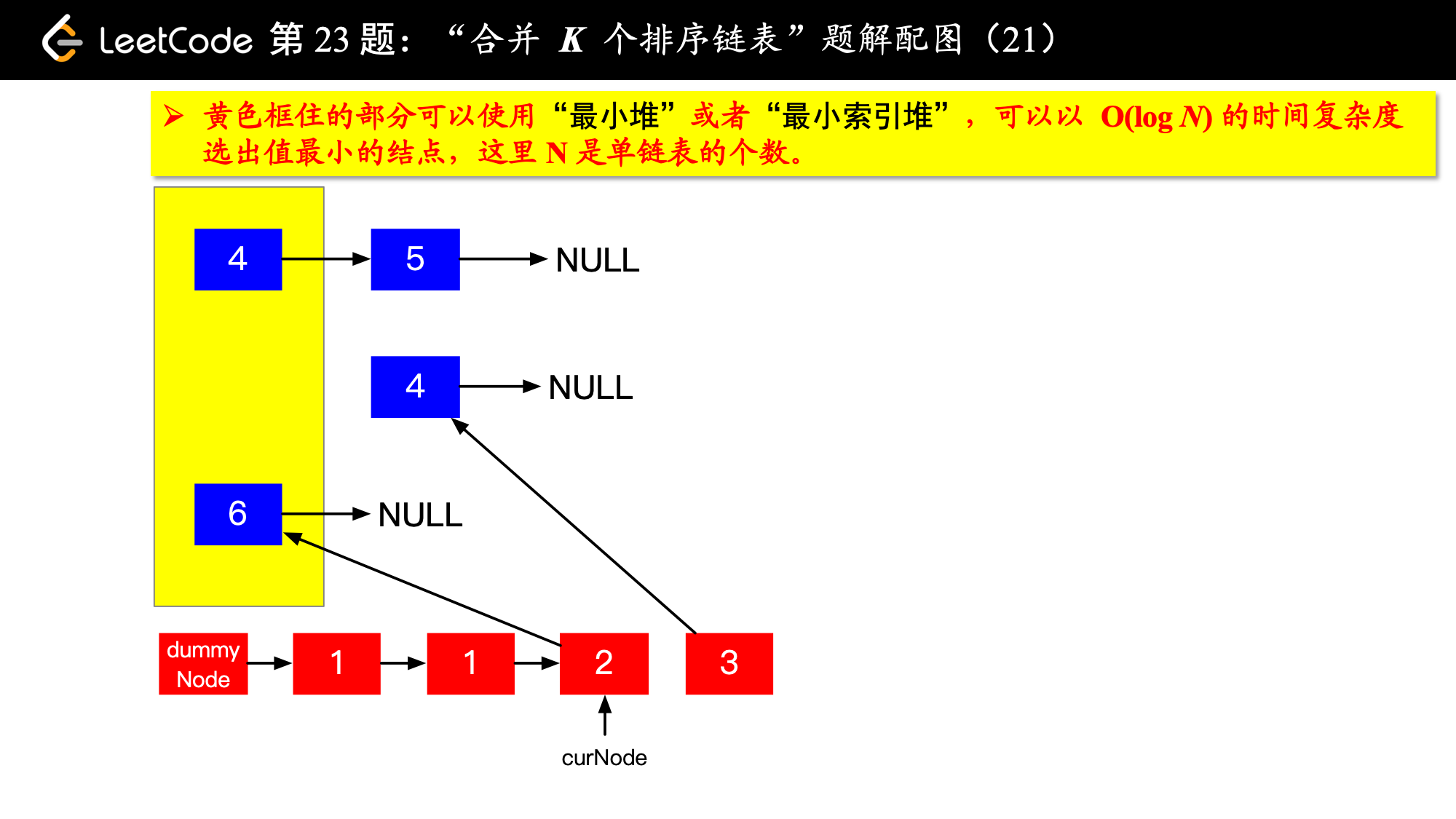
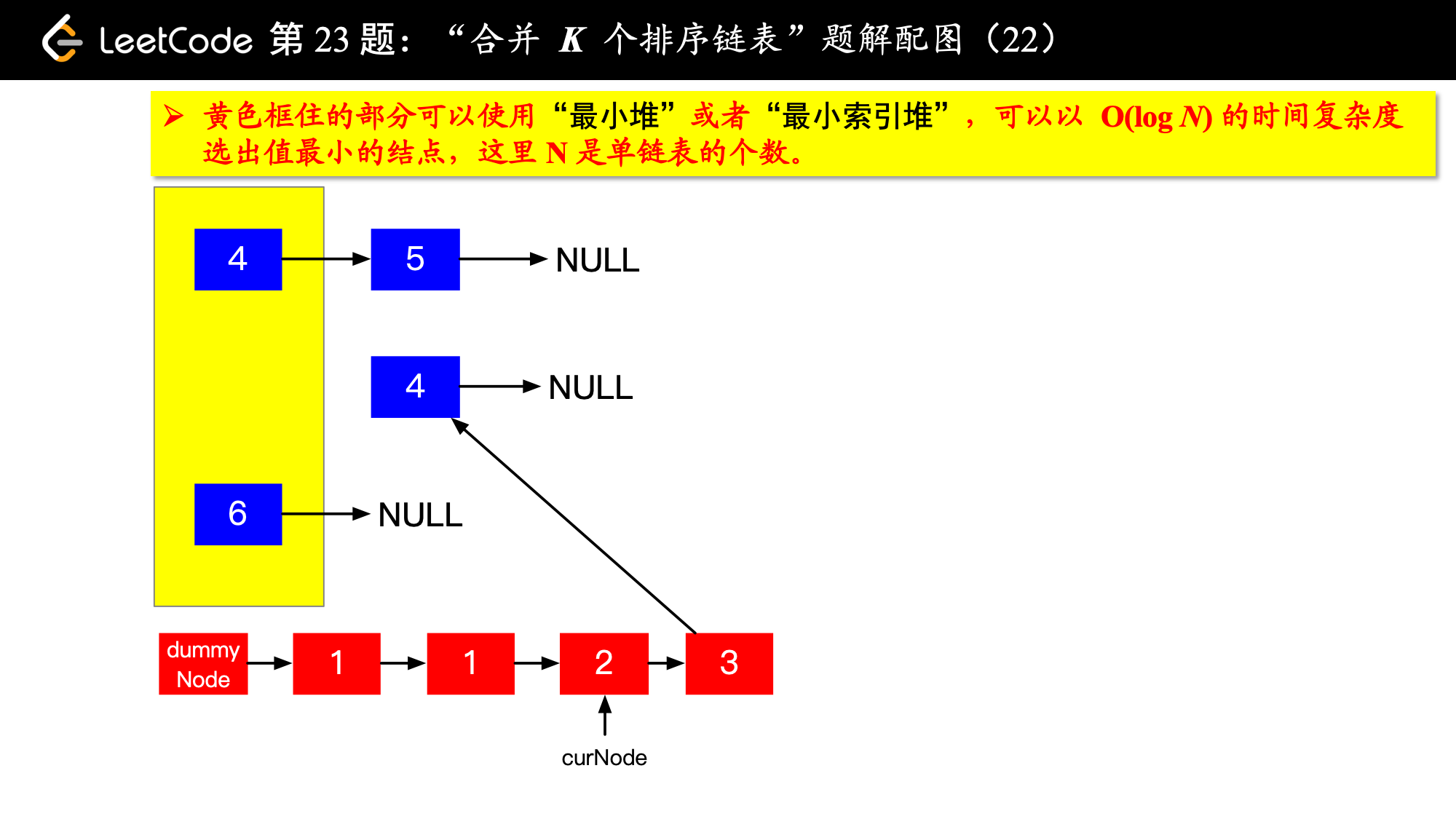
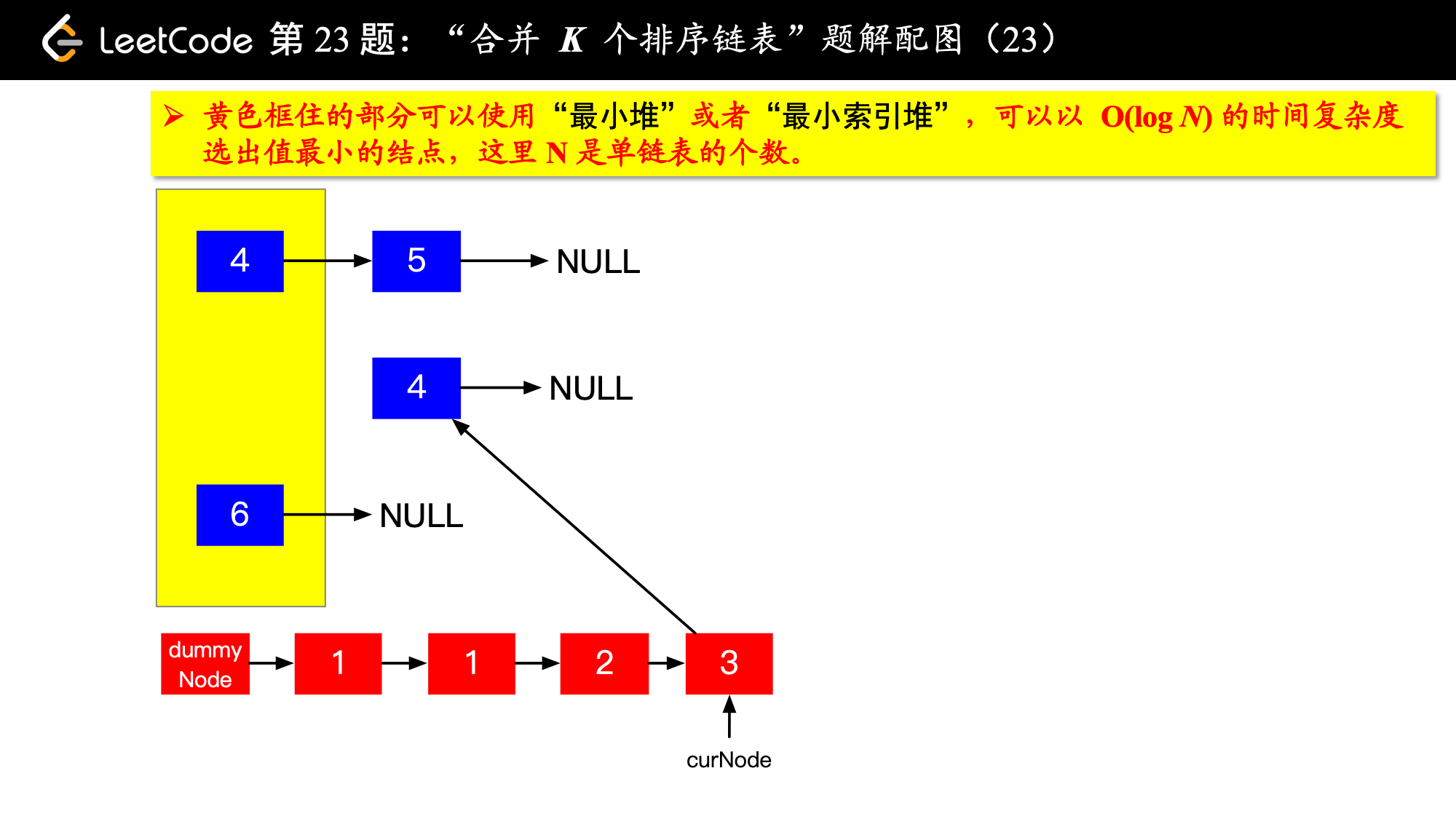
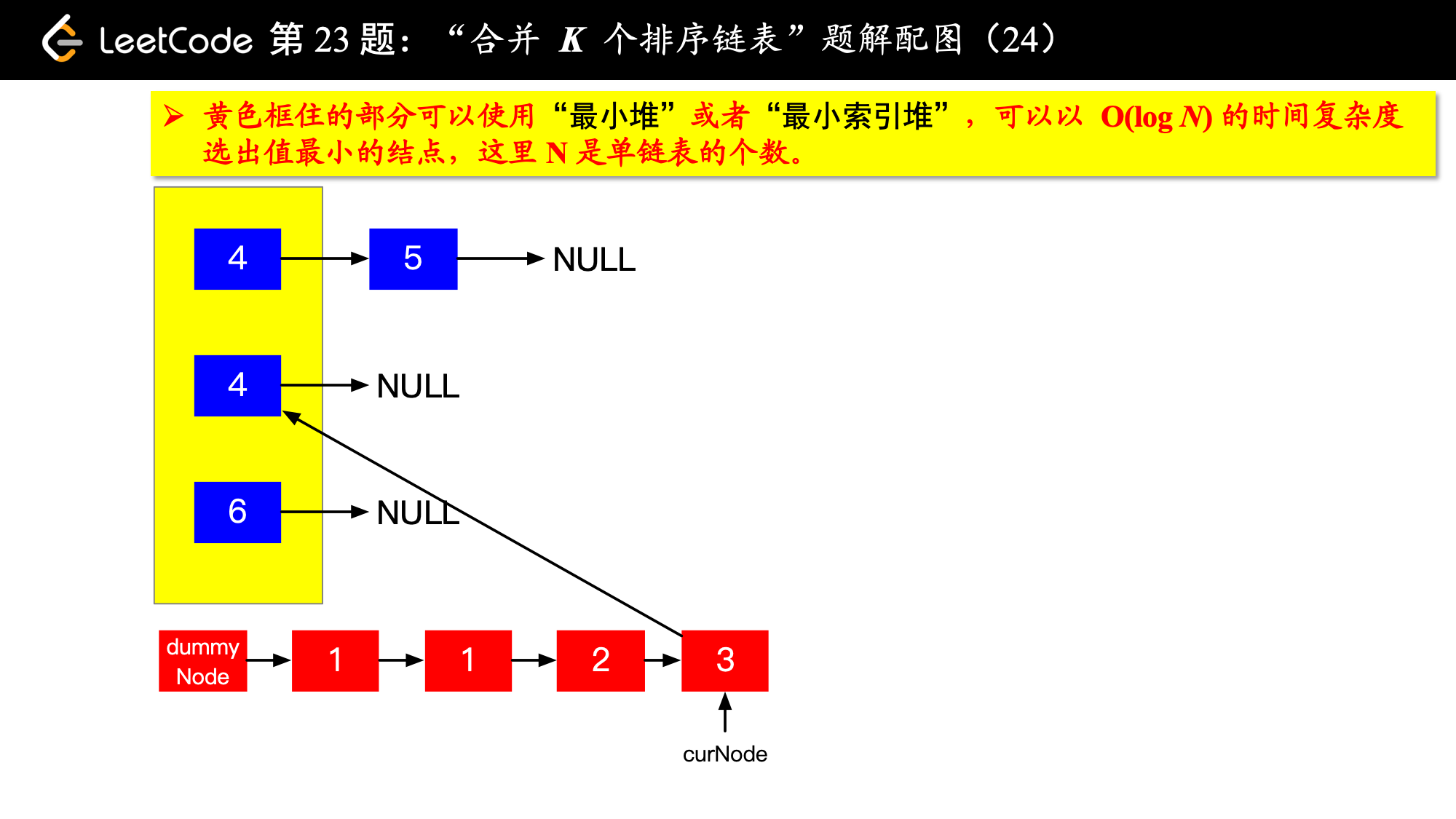
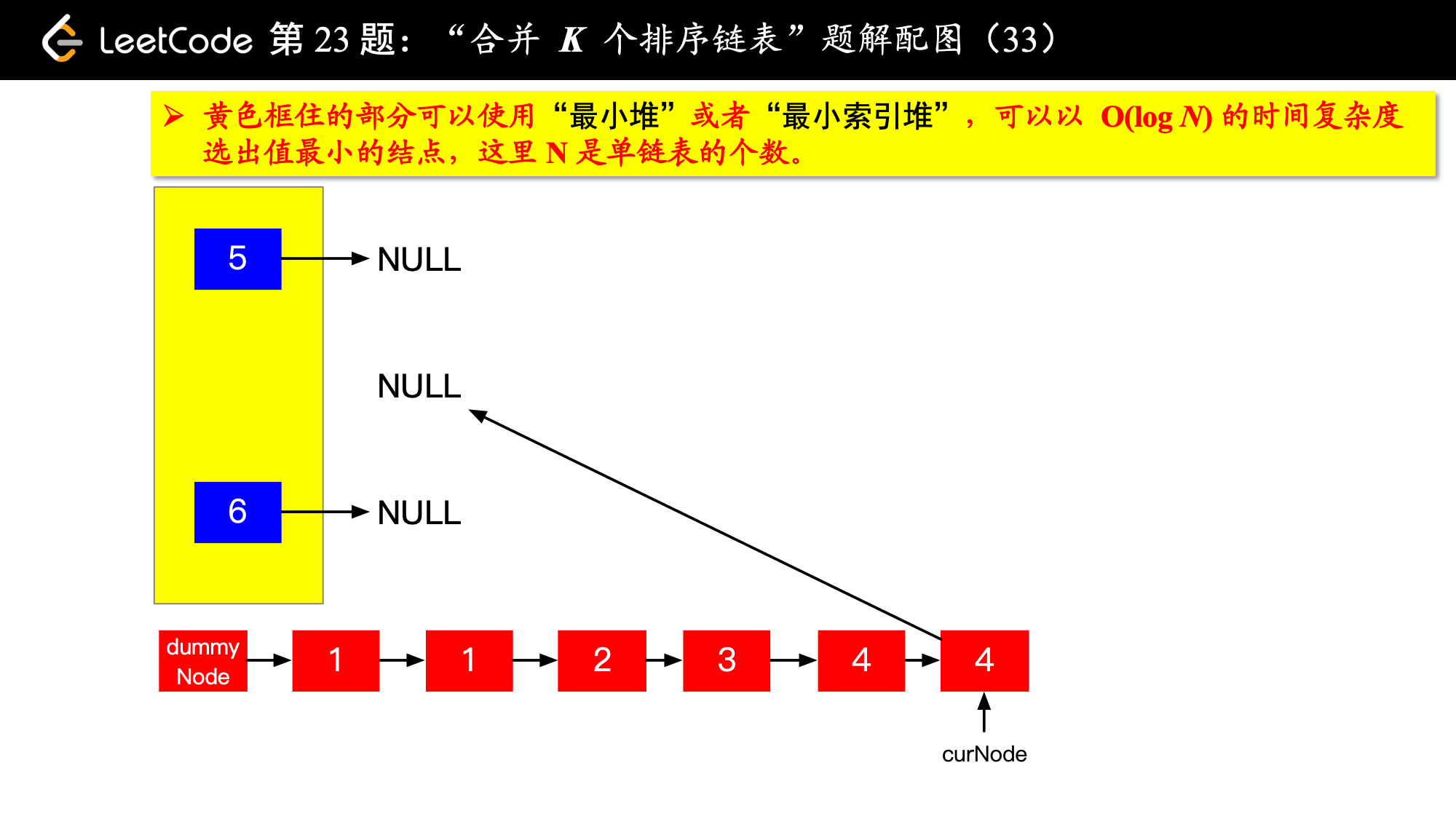
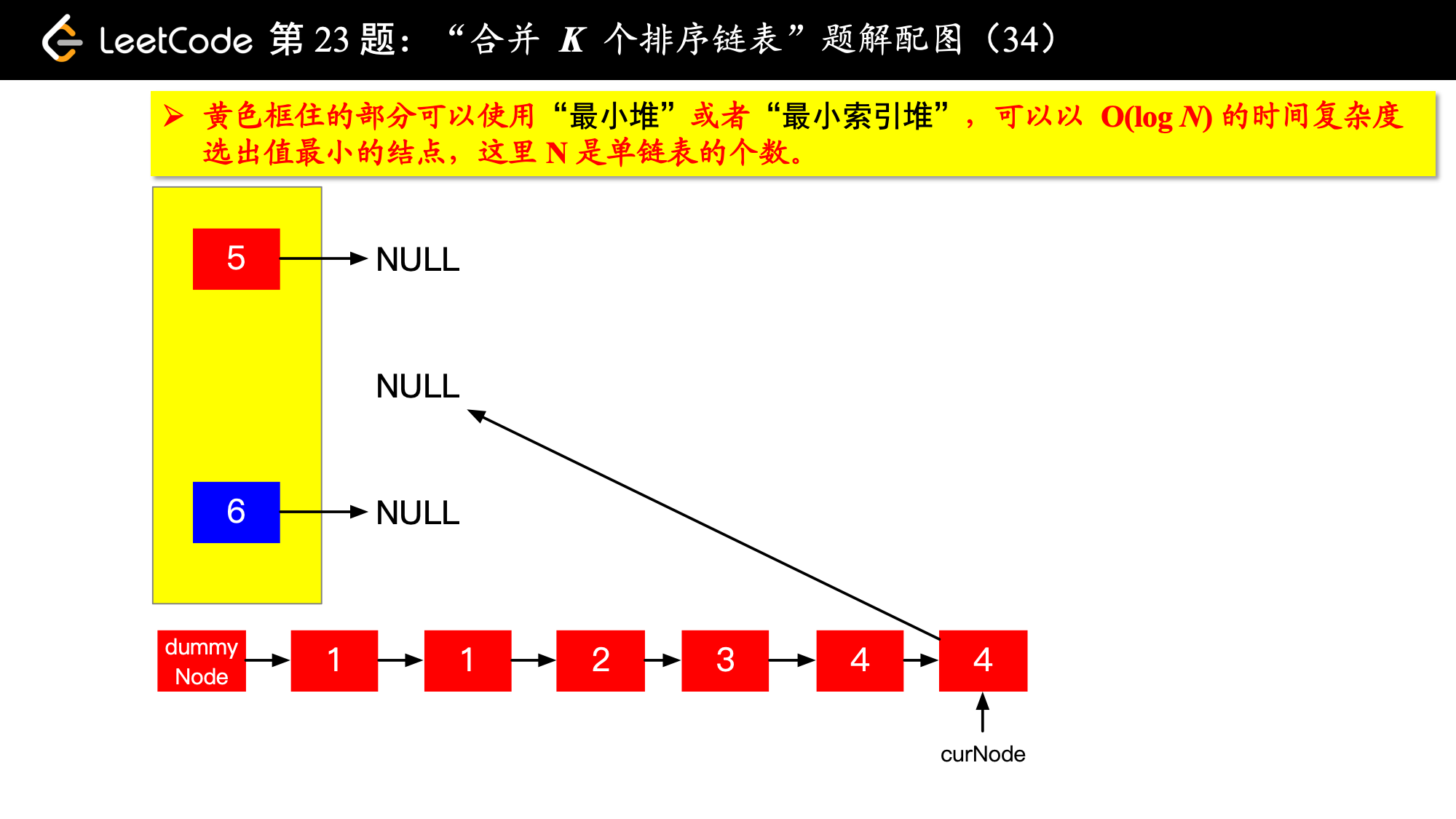
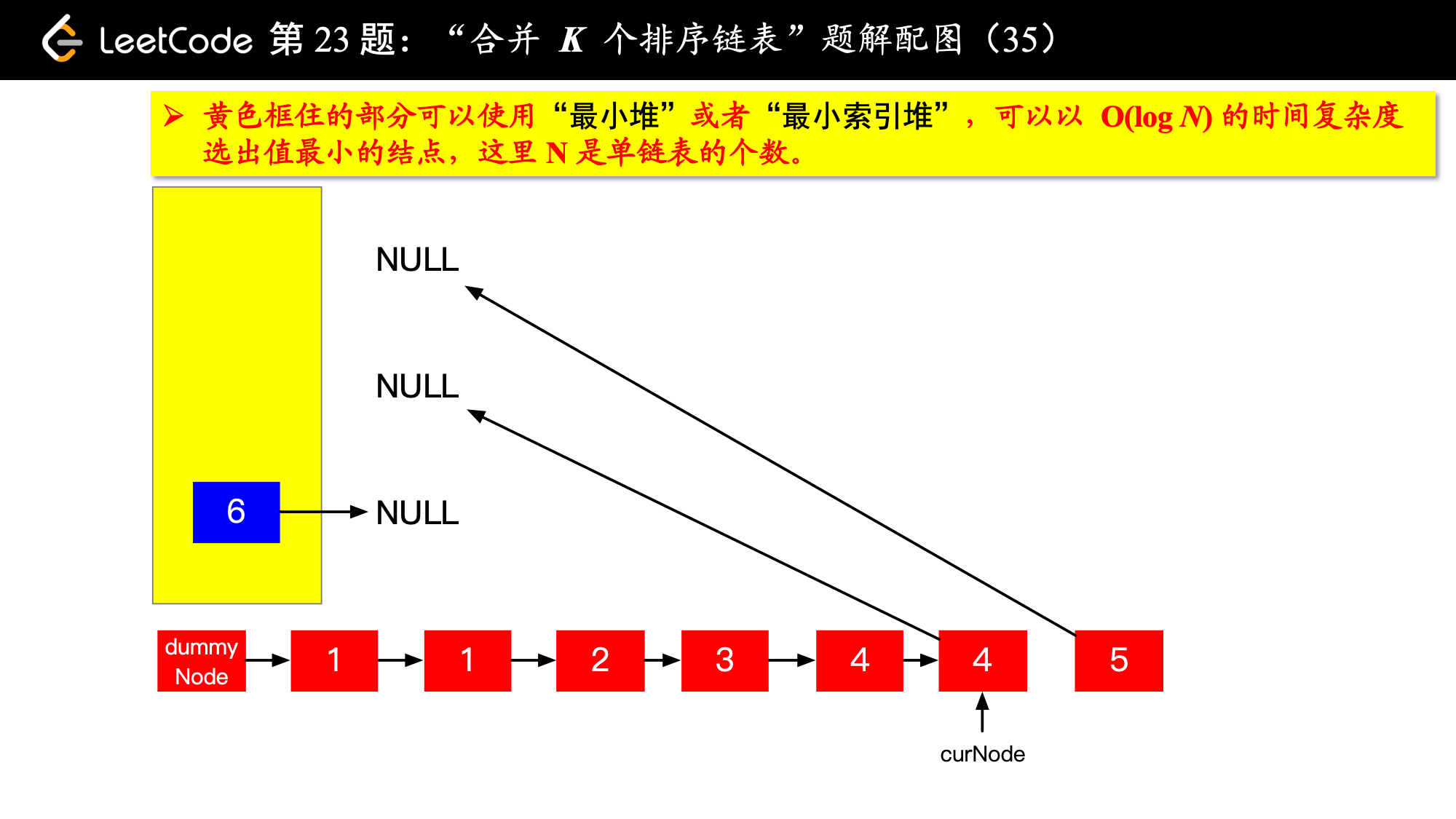
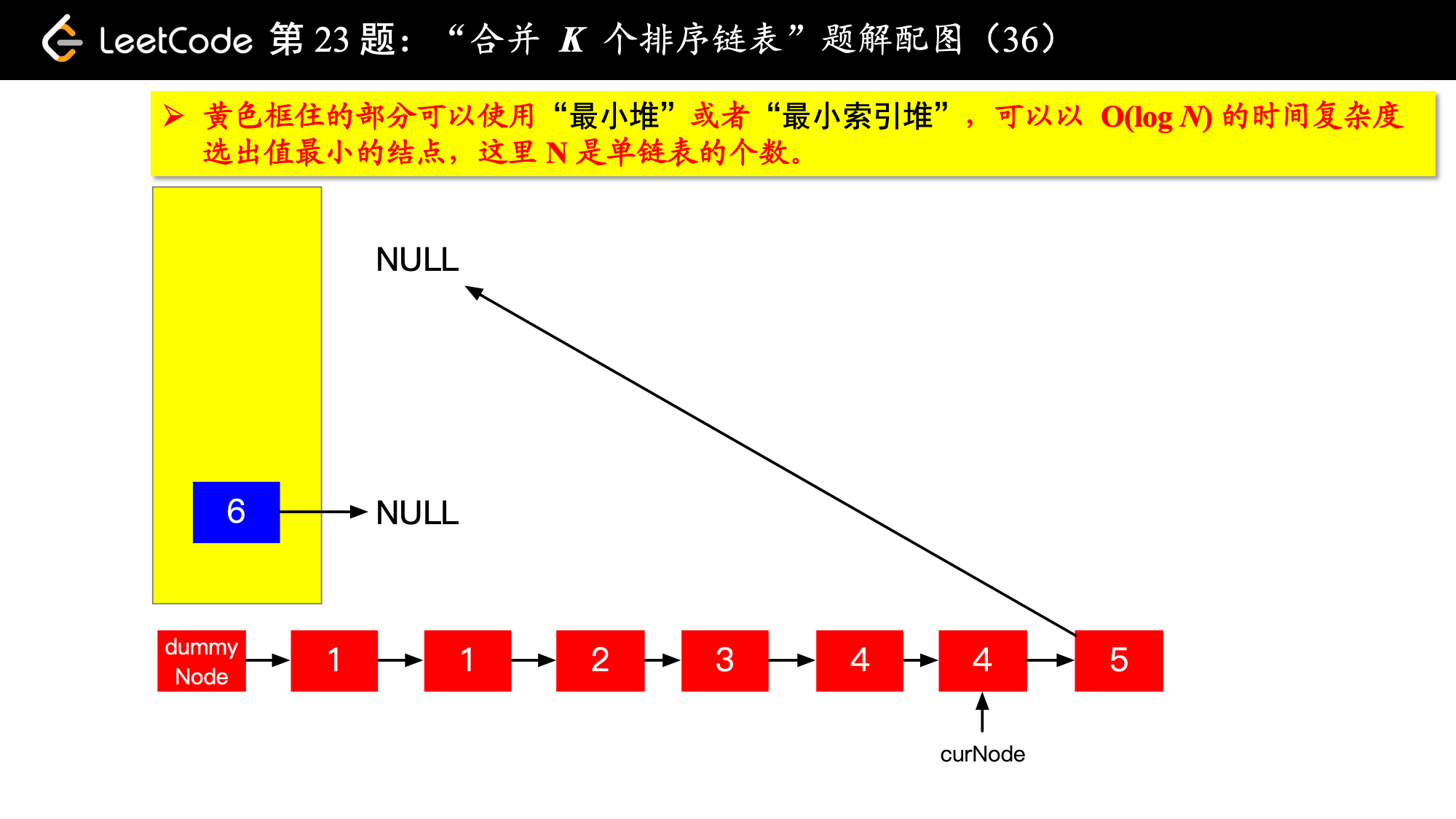
1、由于是 $k$ 个排序链表，那么这 $k$ 个排序的链表头结点中 val 最小的结点就是合并以后的链表中最小的结点；

2、最小结点所在的链表的头结点就要更新了，更新成最小结点的下一个结点（如果有的话），此时还是这 $k$ 个链表，这 $k$ 个排序的链表头结点中 val 最小的结点就是合并以后的链表中第 $2$ 小的结点。

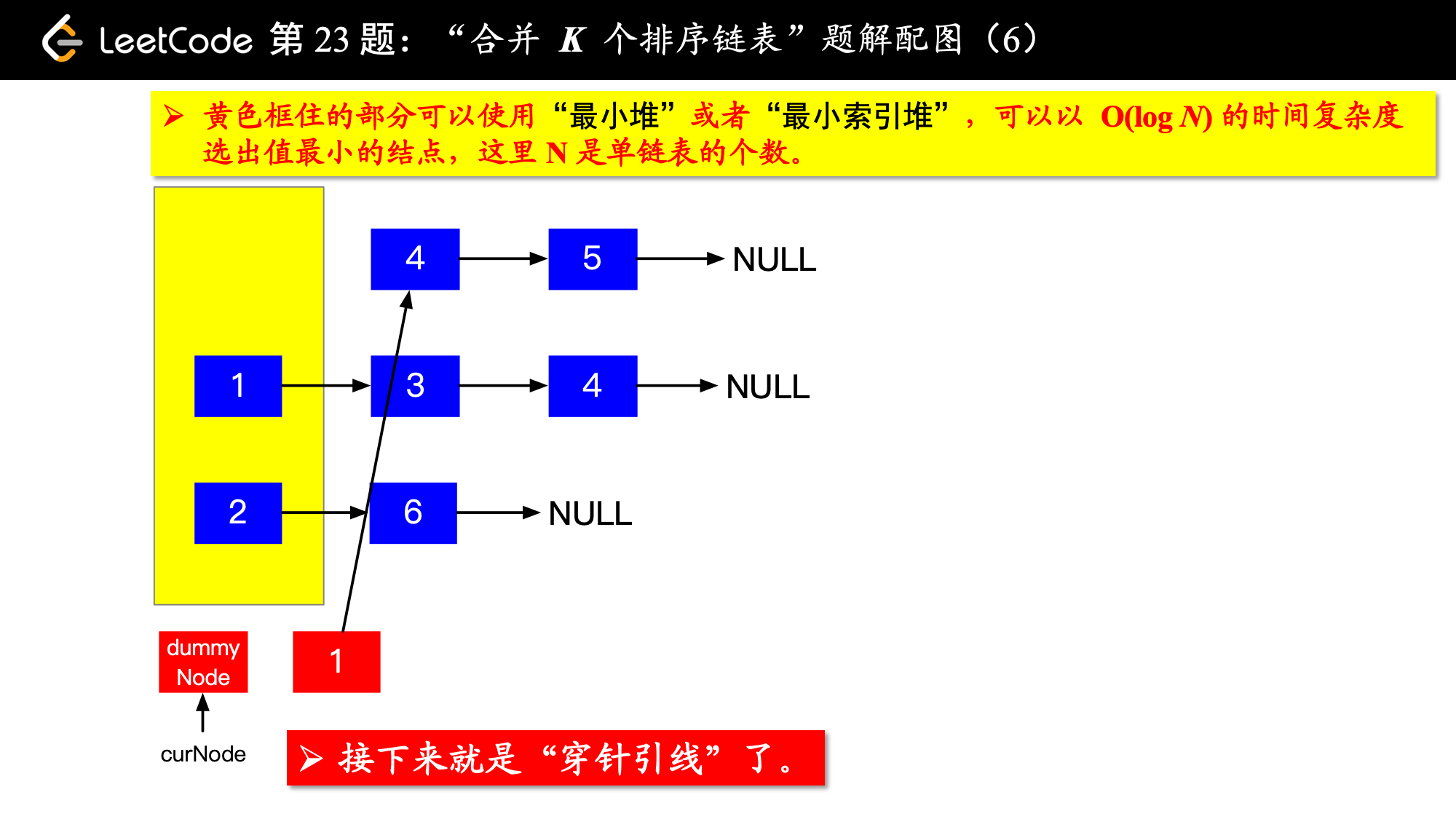
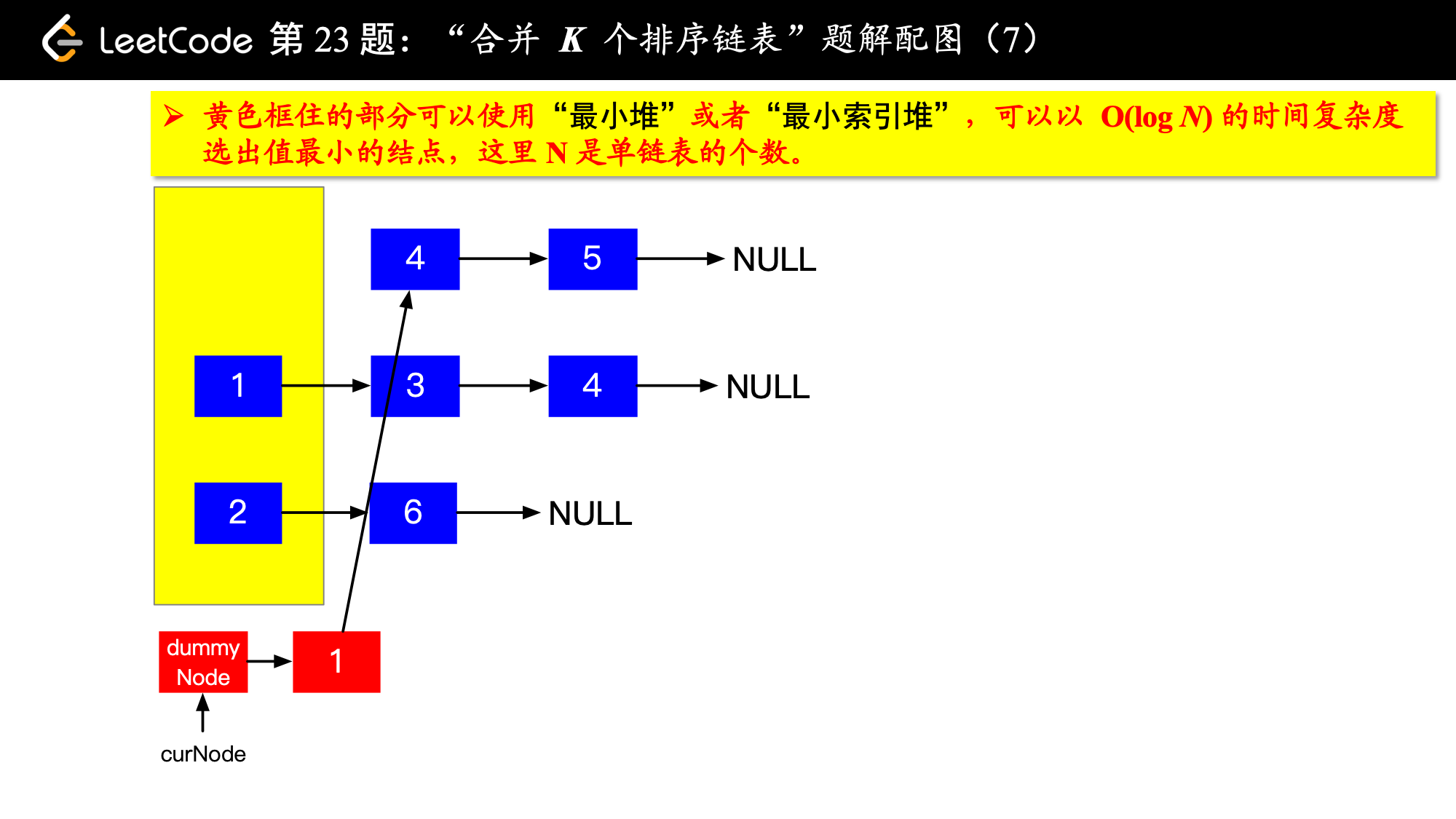
写到这里，我想你应该差不多明白了，我们每一次都从这 $k$ 个排序的链表头结点中拿出 val 最小的结点“穿针引线”成新的链表，这个链表就是题目要求的“合并后的排序链表”。“局部最优，全局就最优”，这不就是贪心算法的思想吗。

这里我们举生活中的例子来理解这个思路。

假设你是一名体育老师，有 $3$ 个班的学生，他们已经按照身高从矮到高排好成了 $3$ 列纵队，现在要把这 $3$ 个班的学生也按照身高从矮到高排列 $1$ 列纵队。我们可以这么做：

1、让 $3$ 个班的学生按列站在你的面前，这时你能看到站在队首的学生的全身；
2、每一次队首的 $3$ 名同学，请最矮的同学出列到“队伍4”（即我们最终认为排好序的队列），出列的这一列的后面的所有同学都向前走一步（其实走不走都行，只要你能比较出站在你面前的 3 位在队首的同学同学的高矮即可）；
3、重复第 2 步，直到 $3$ 个班的同学全部出列完毕。

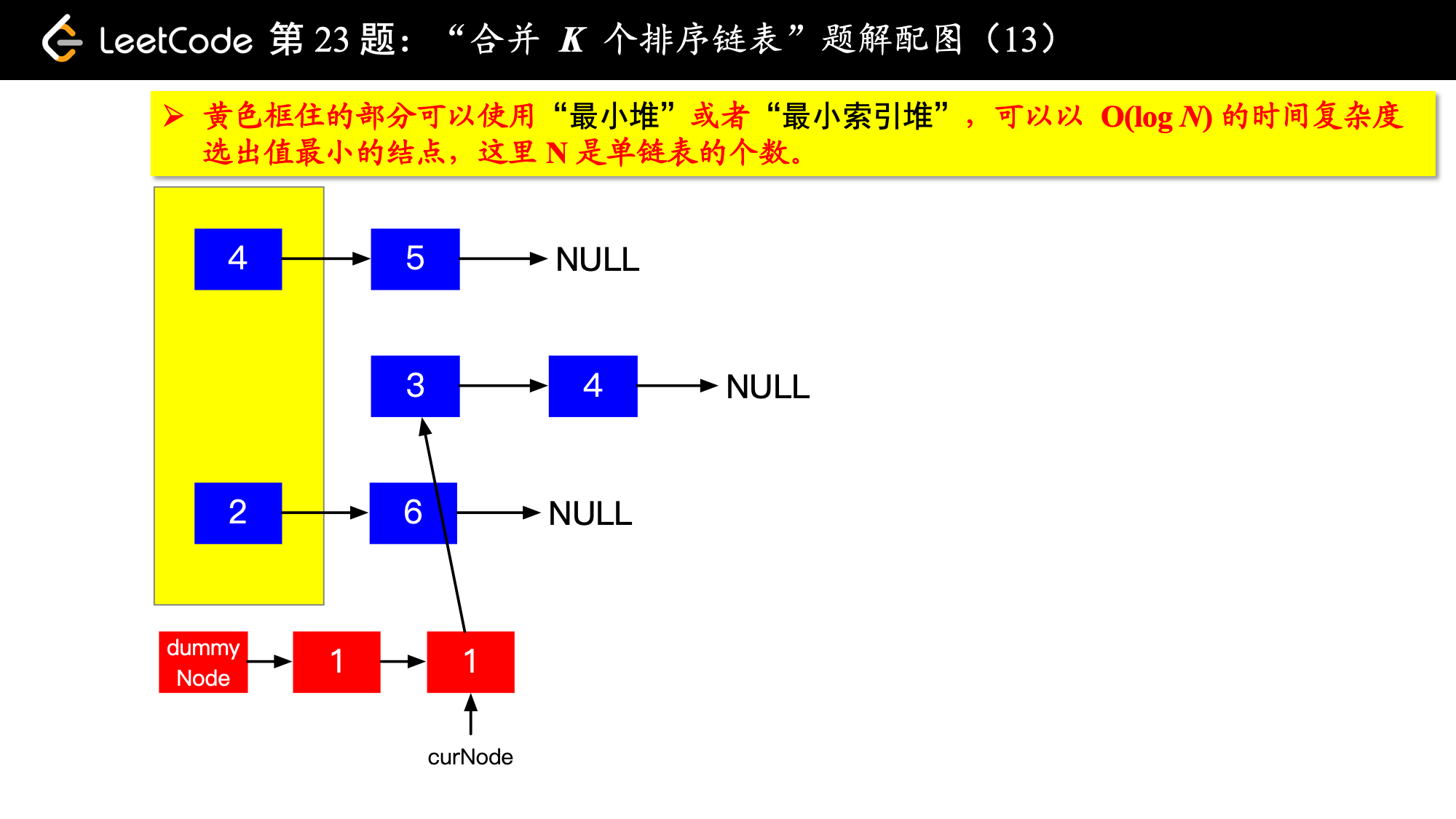
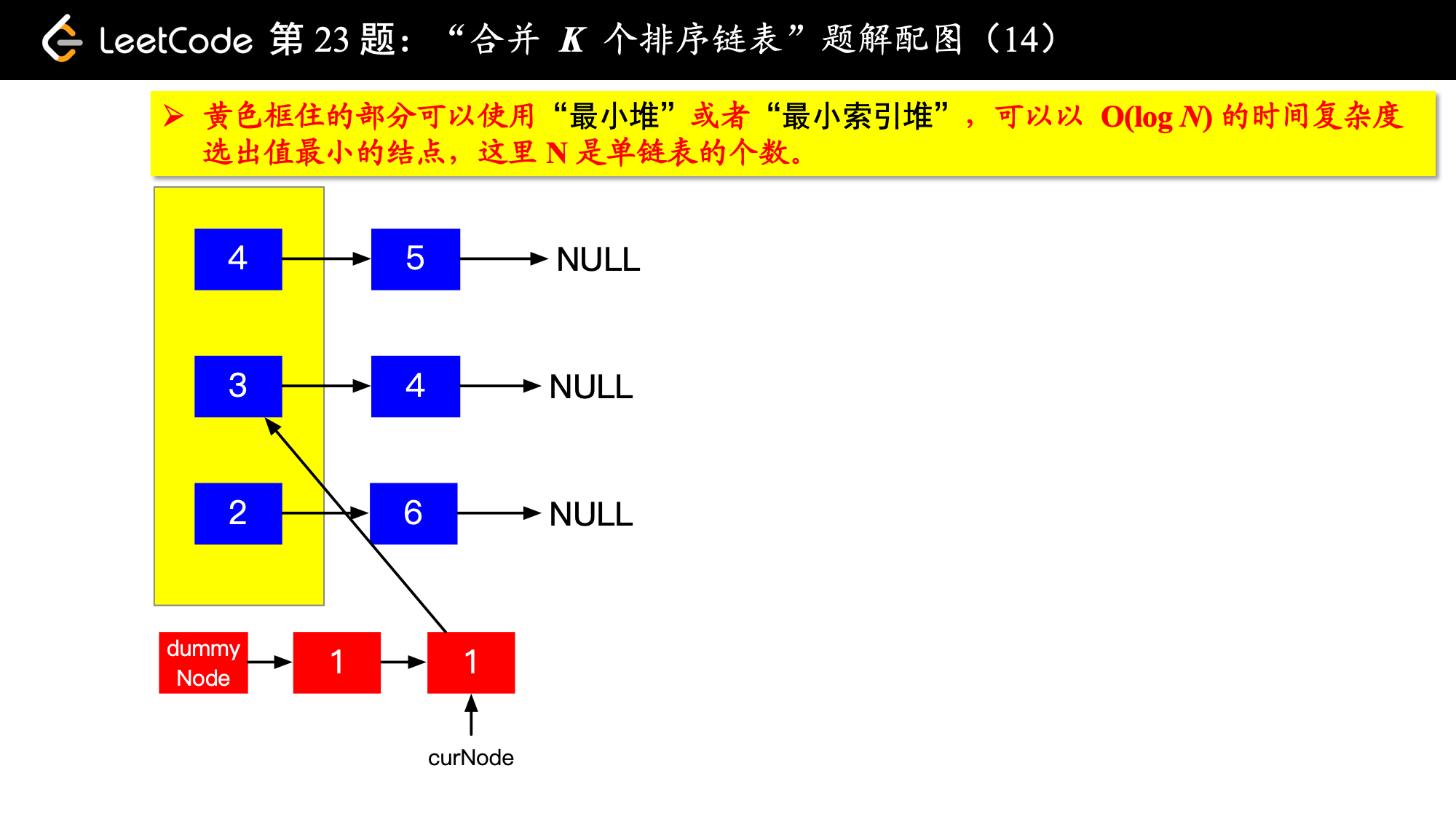
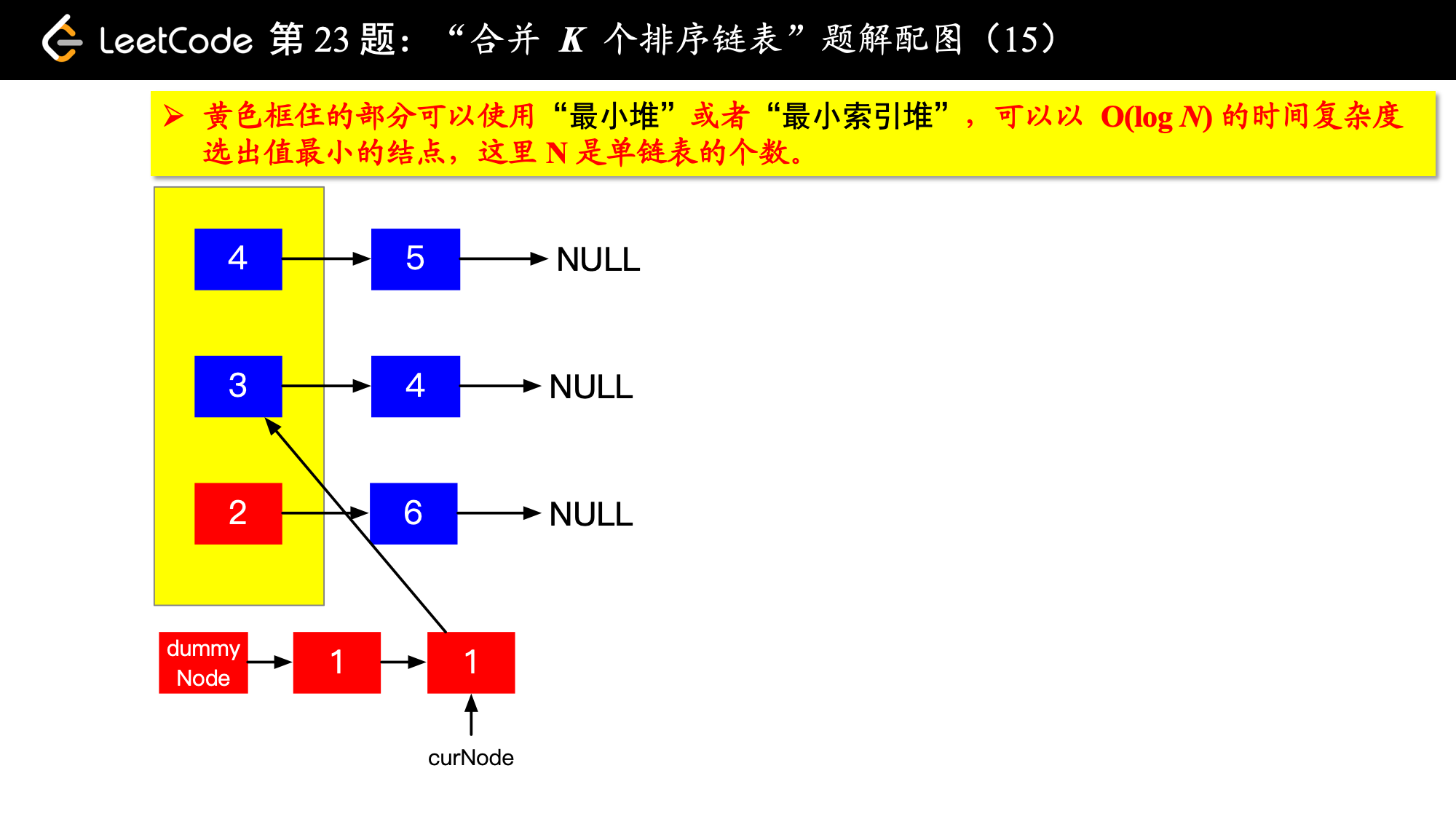
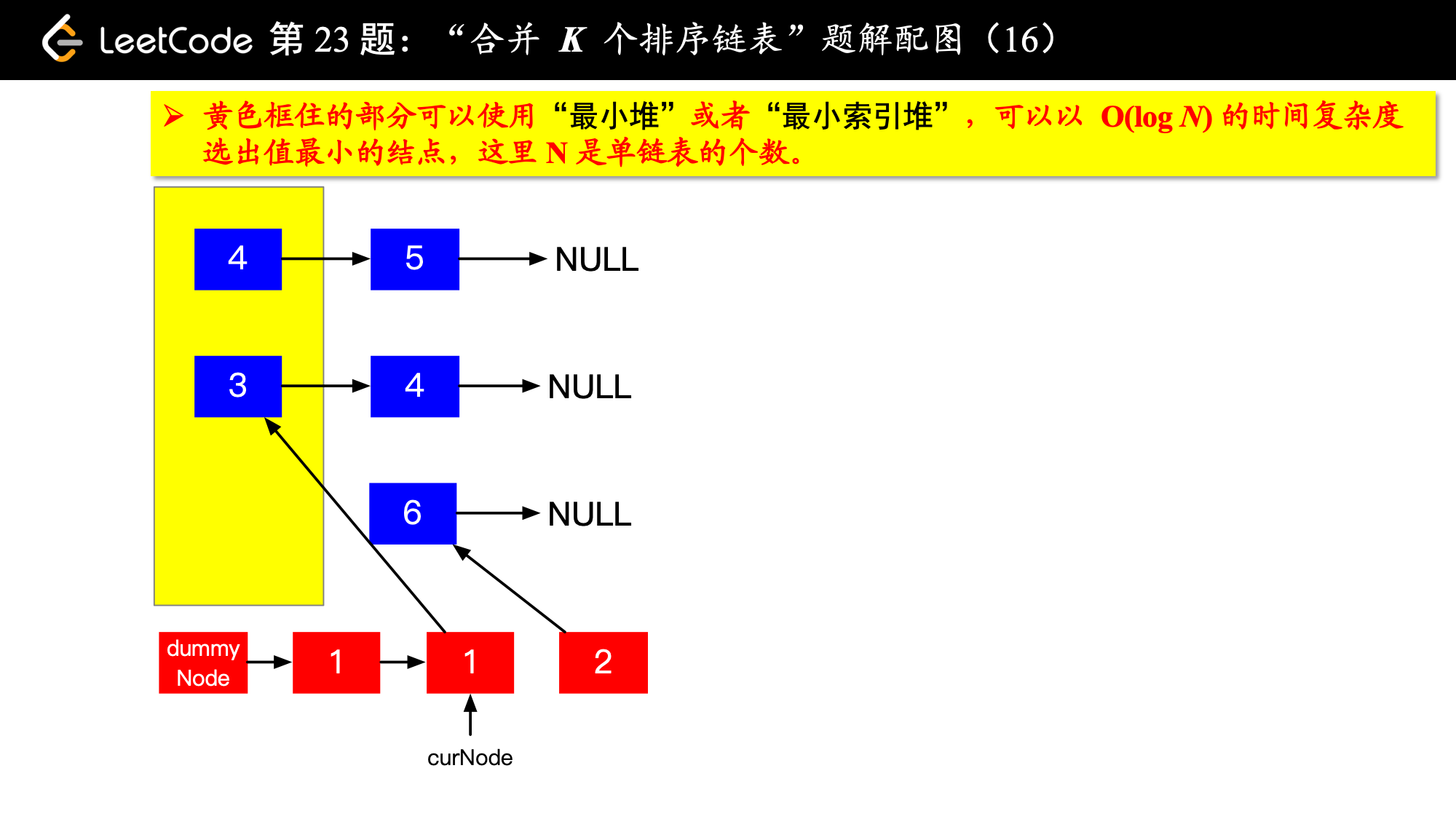
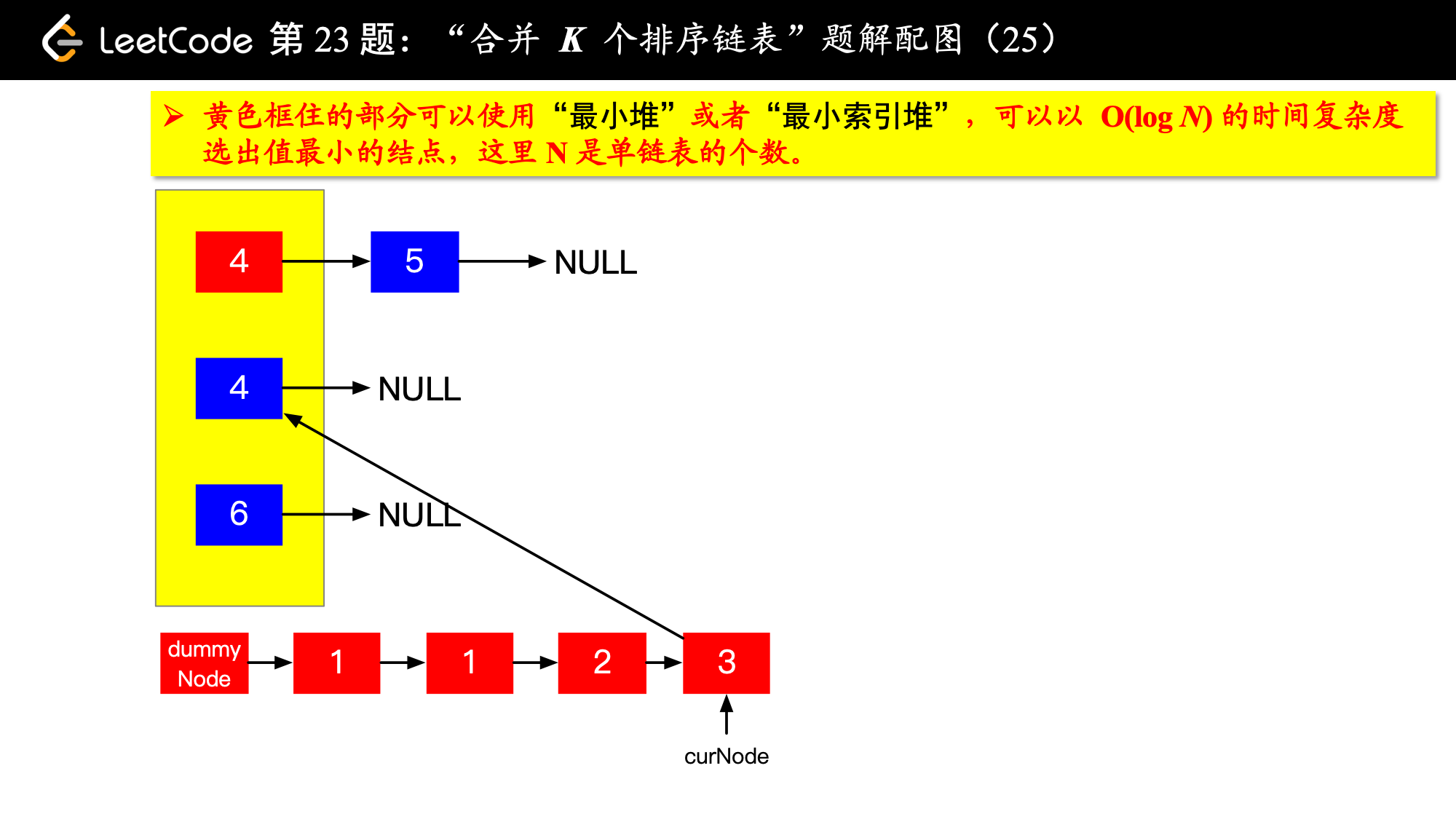
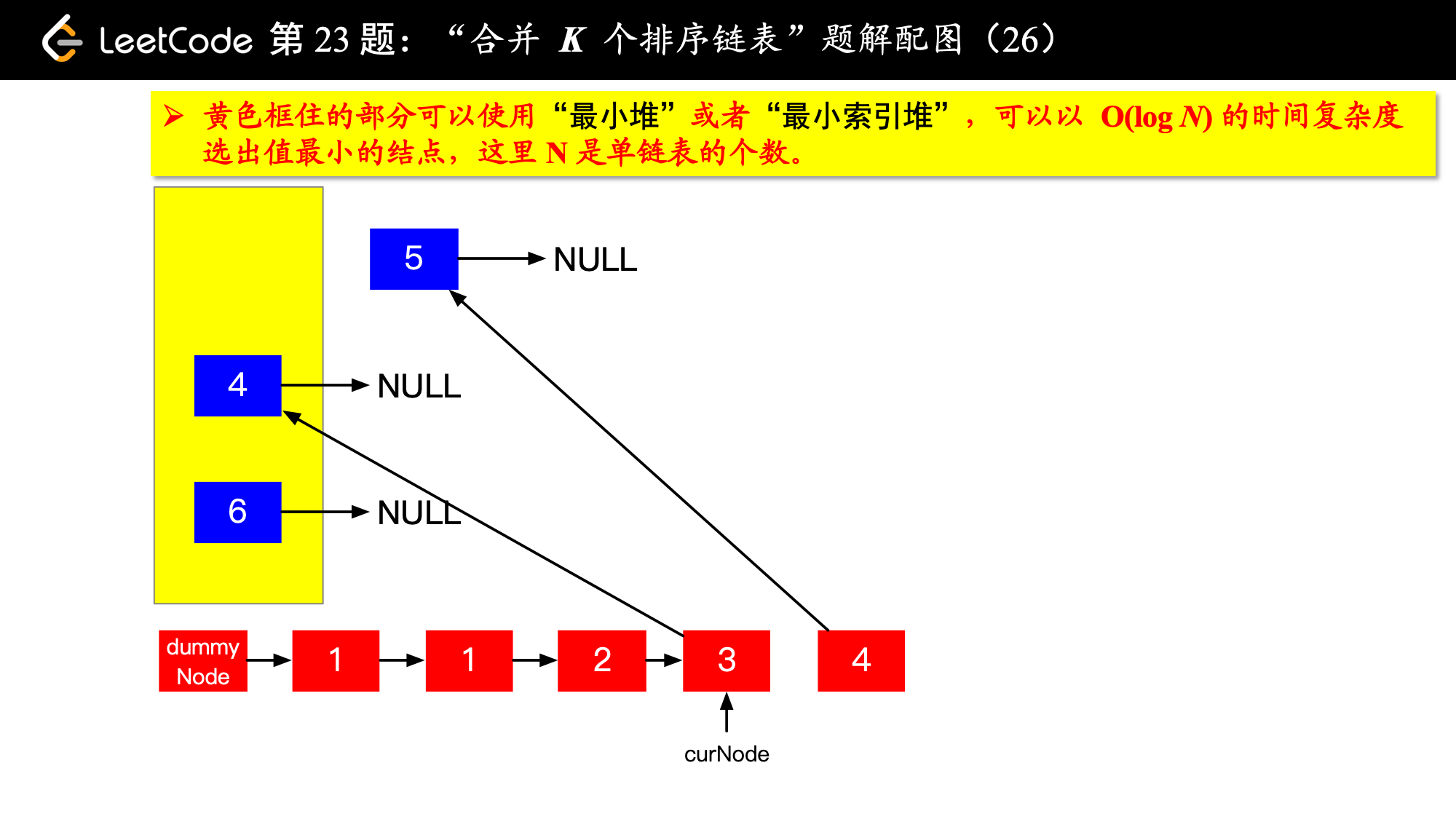
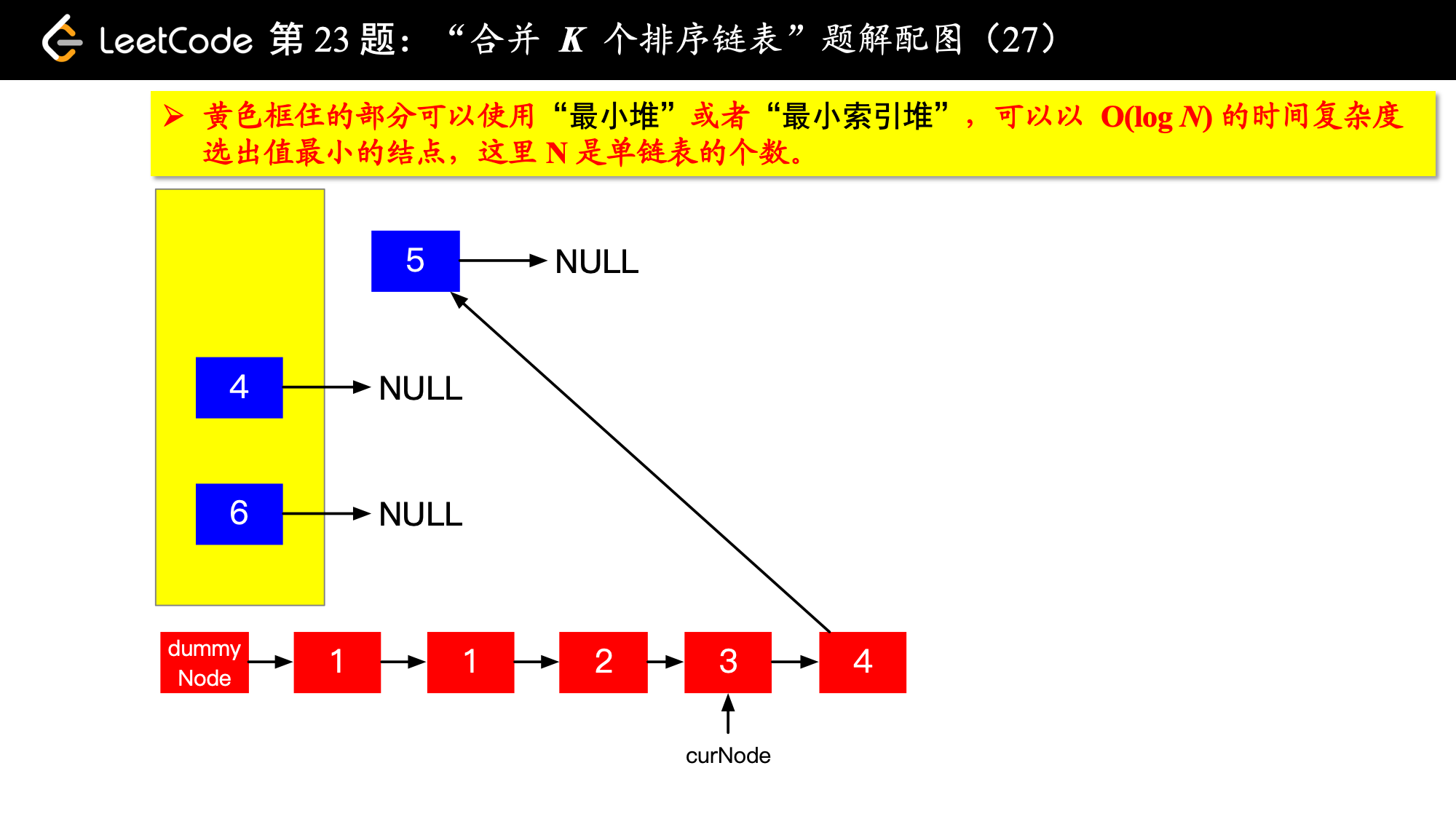
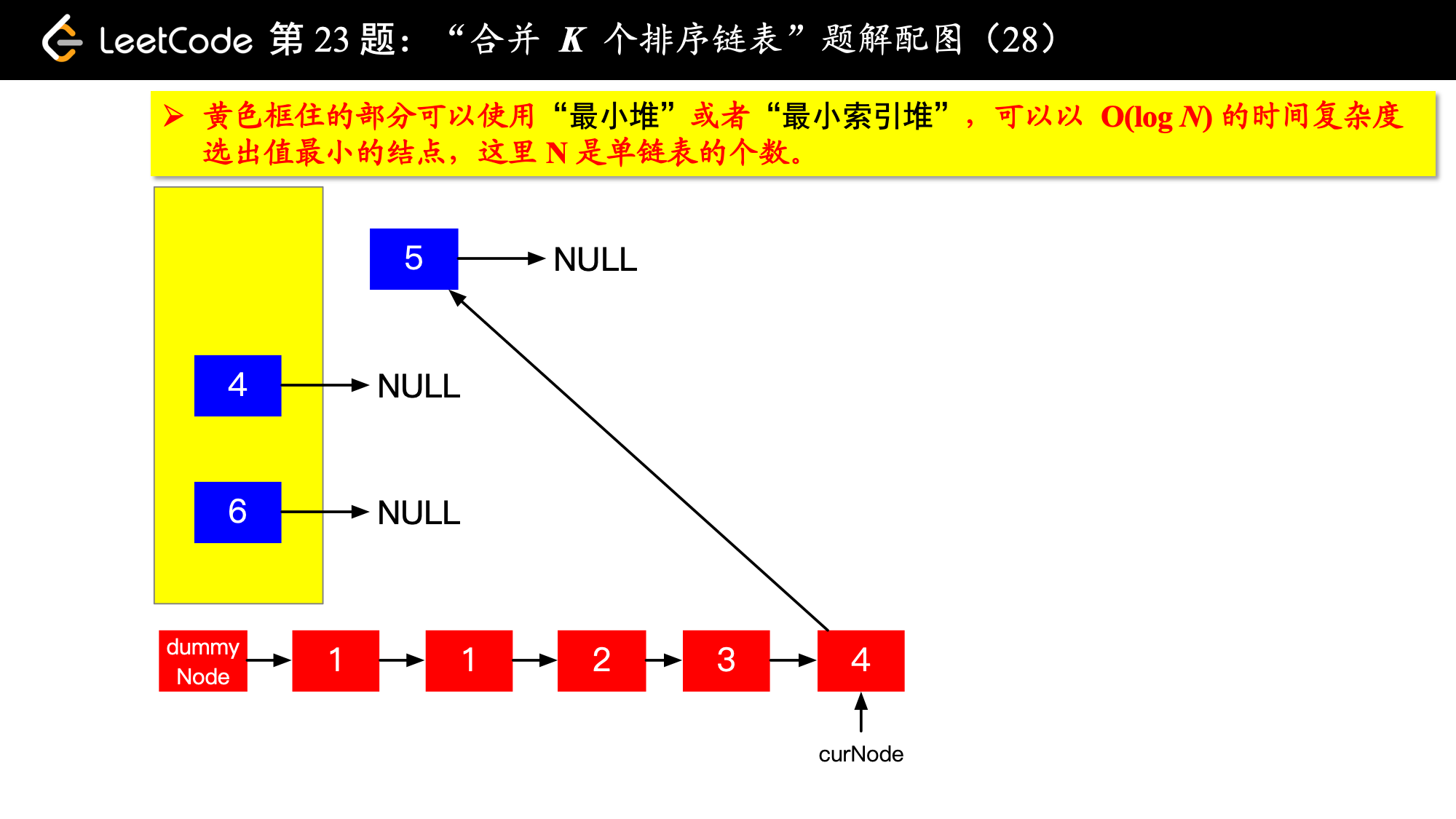
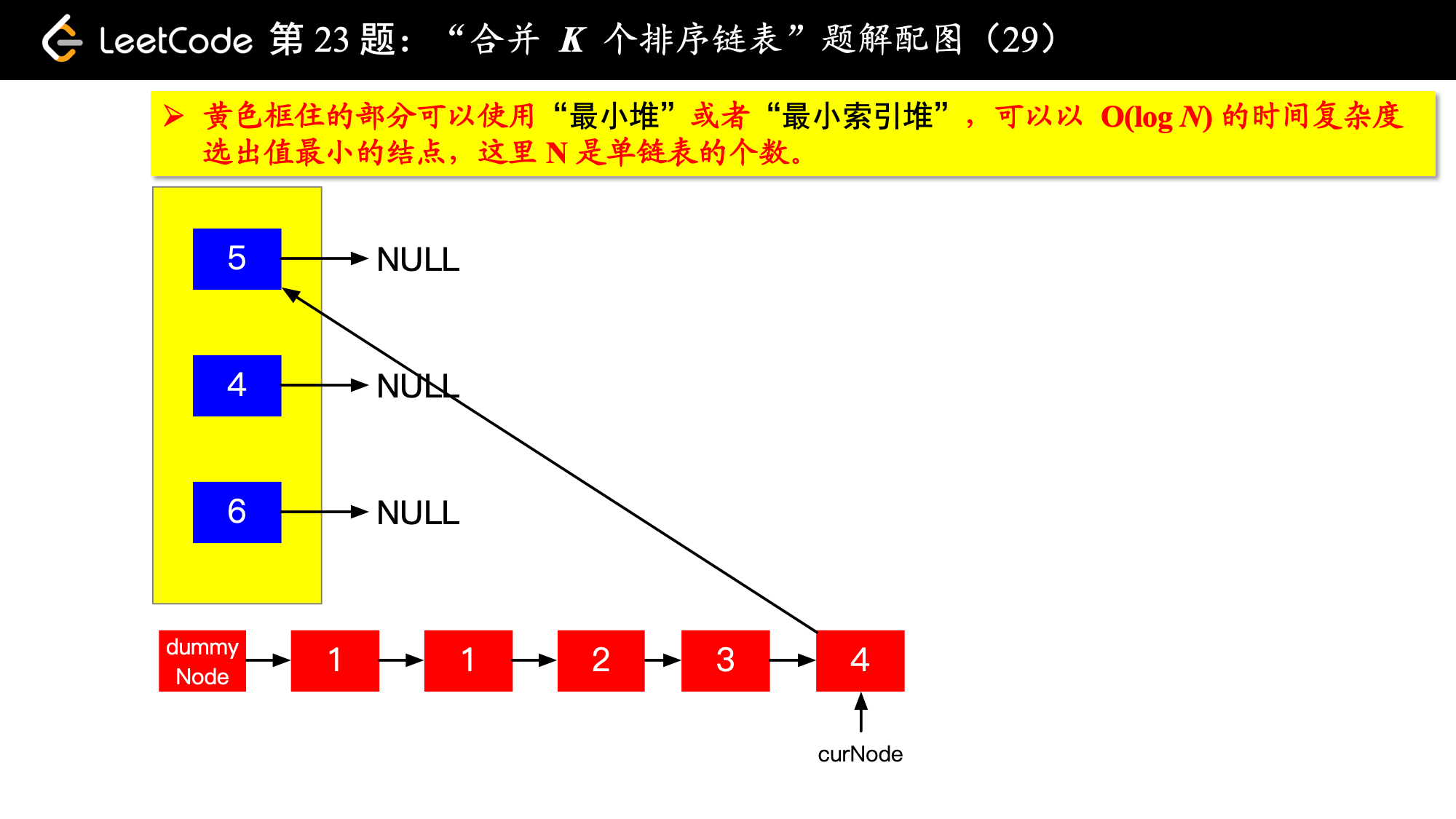
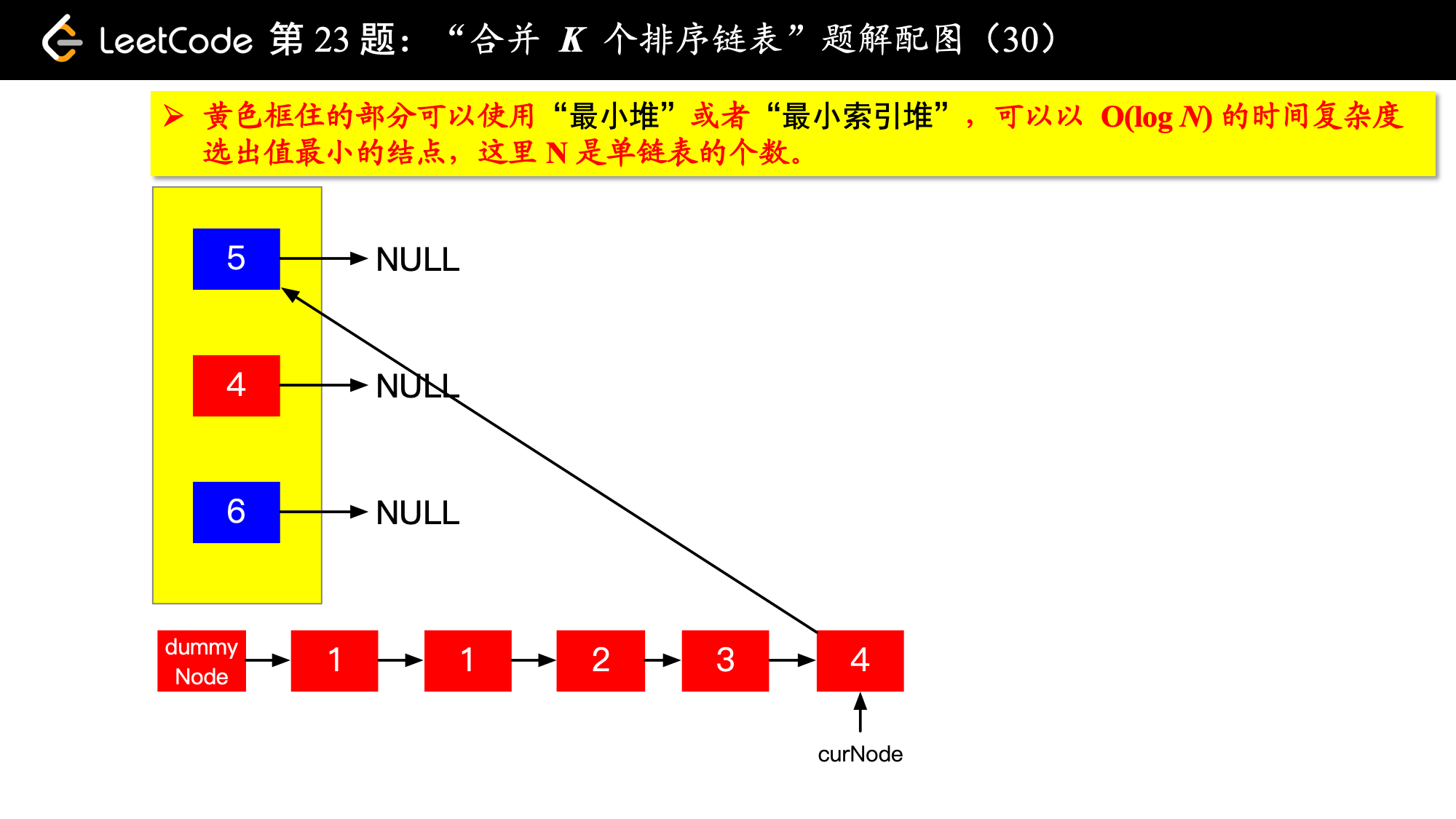
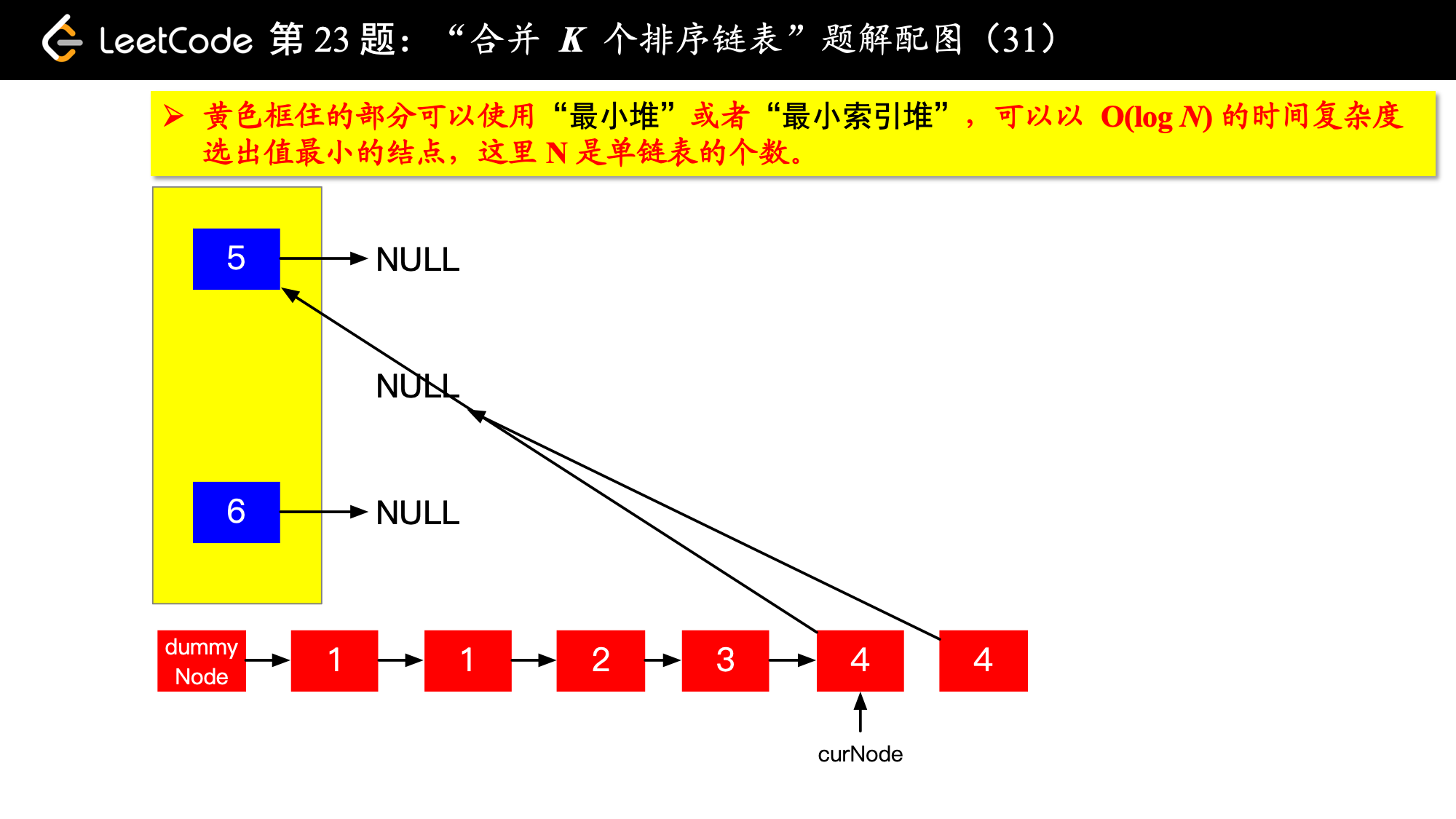
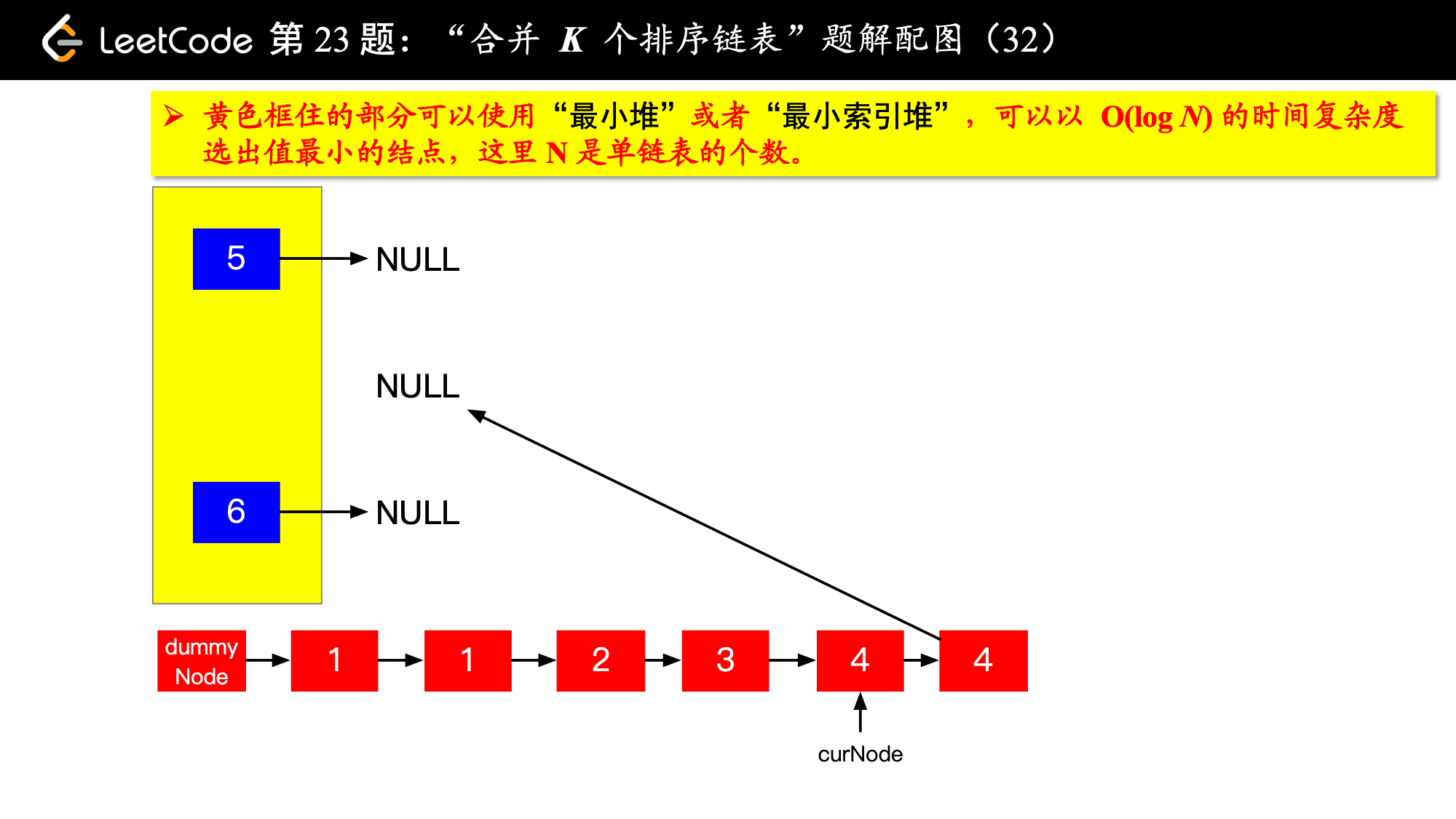
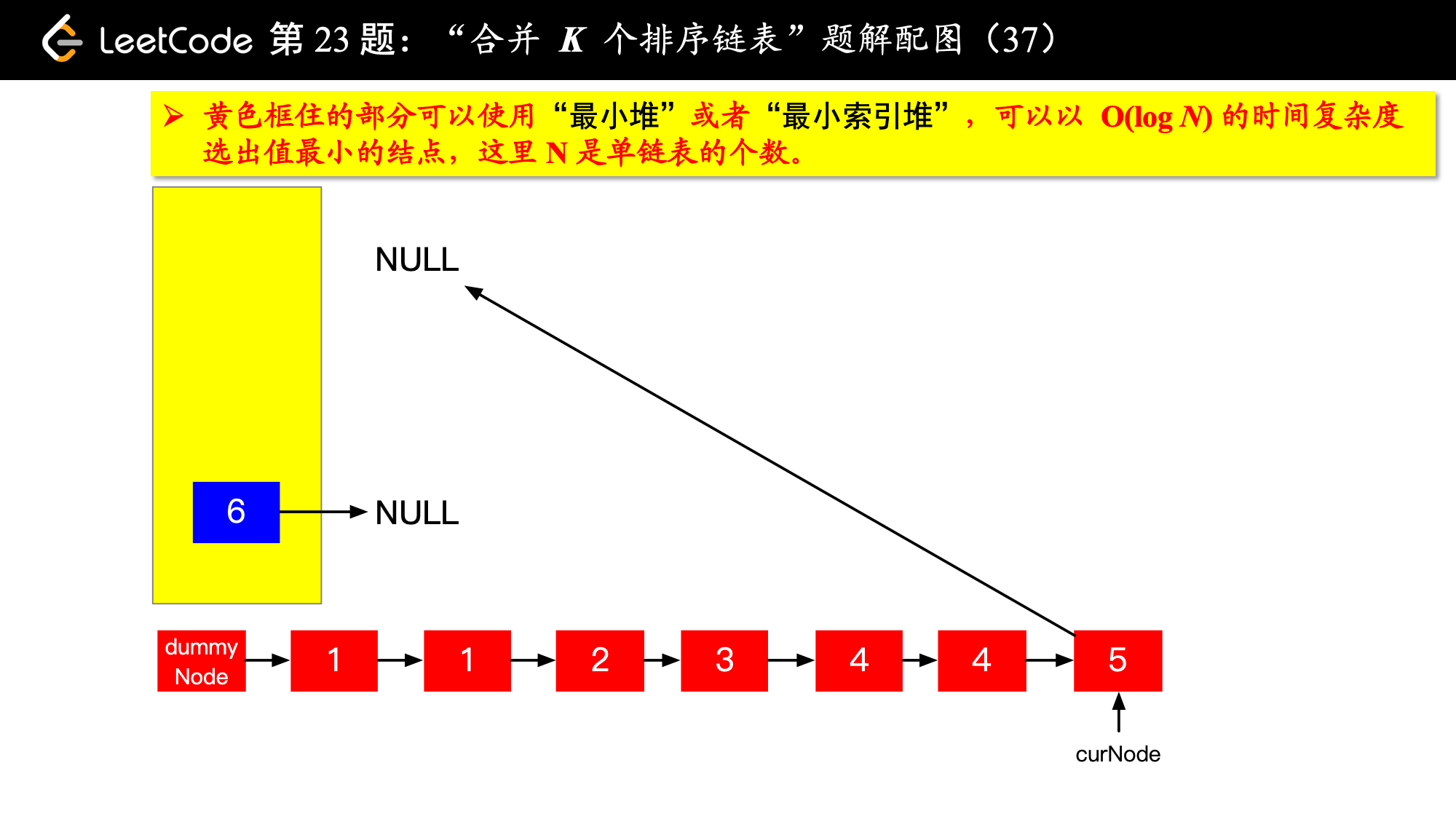
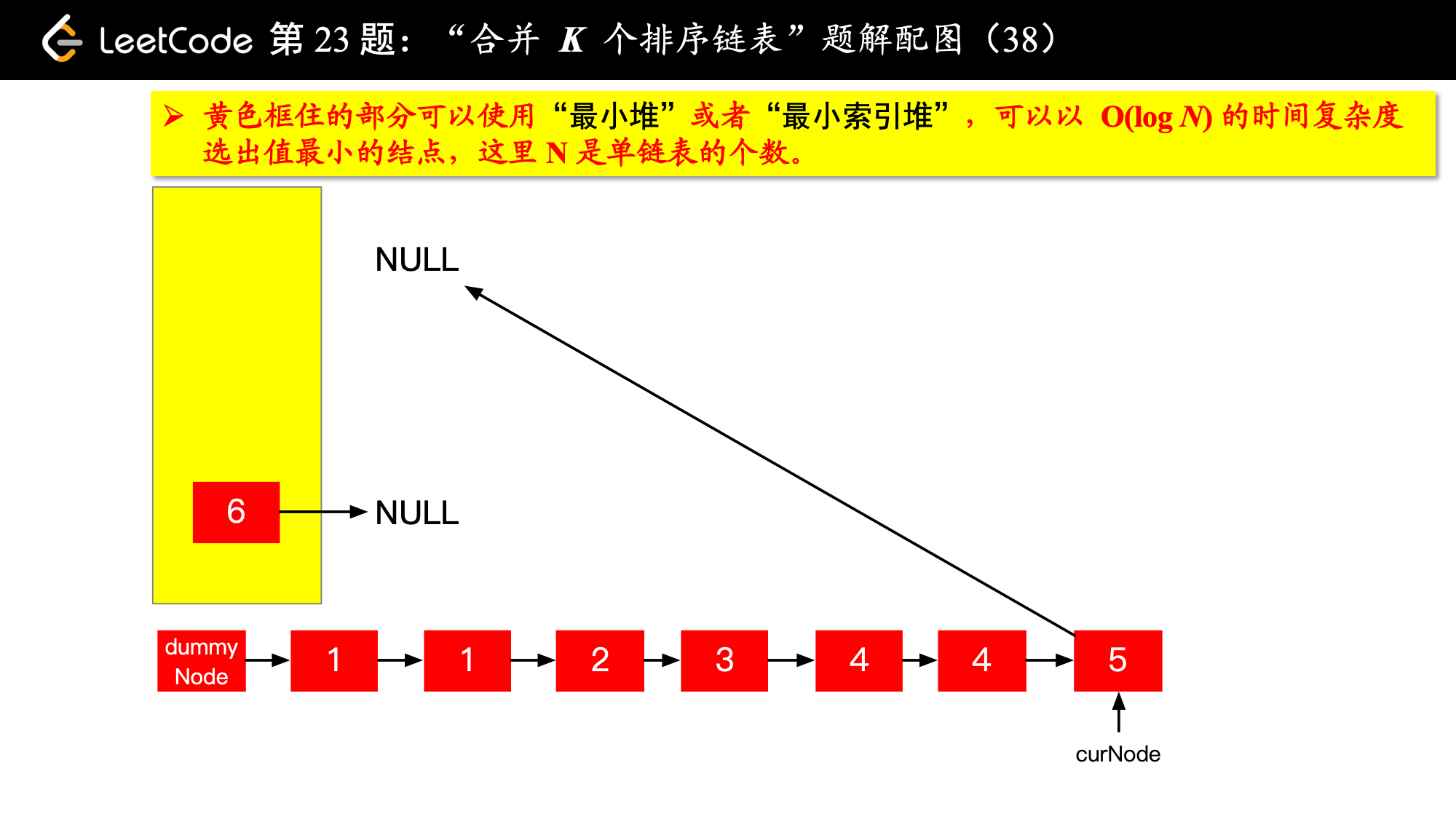
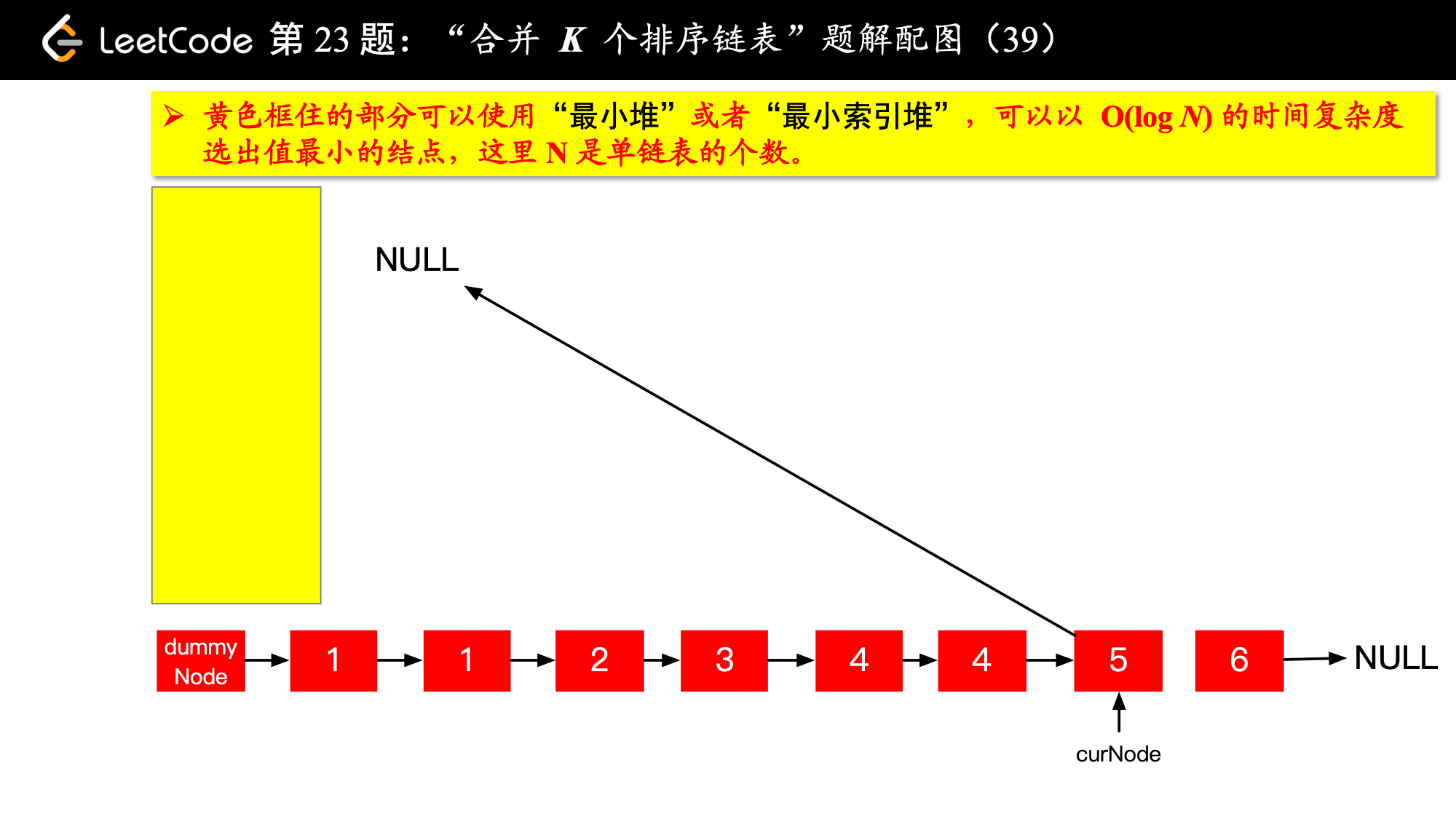
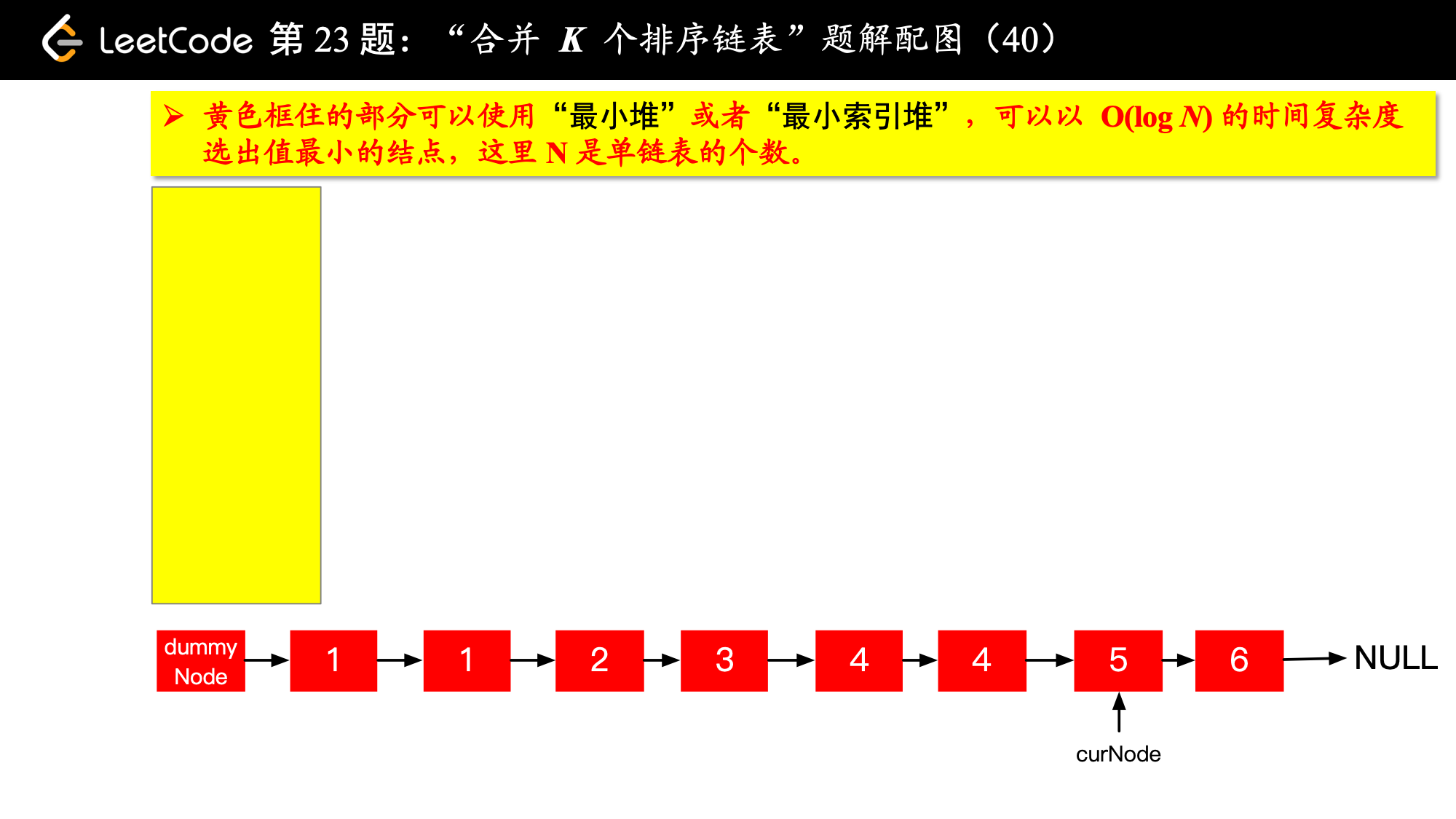
具体实现的时候，“每一次队首的 $3$ 名同学，请最矮的同学出列”这件事情可以交给优先队列（最小堆、最小索引堆均可）去完成。在连续的两次出队之间完成“穿针引线”的工作。

下面的图解释了上面的思路。

（温馨提示：下面的幻灯片中，有几页上有较多的文字，可能需要您停留一下，可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。）

,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

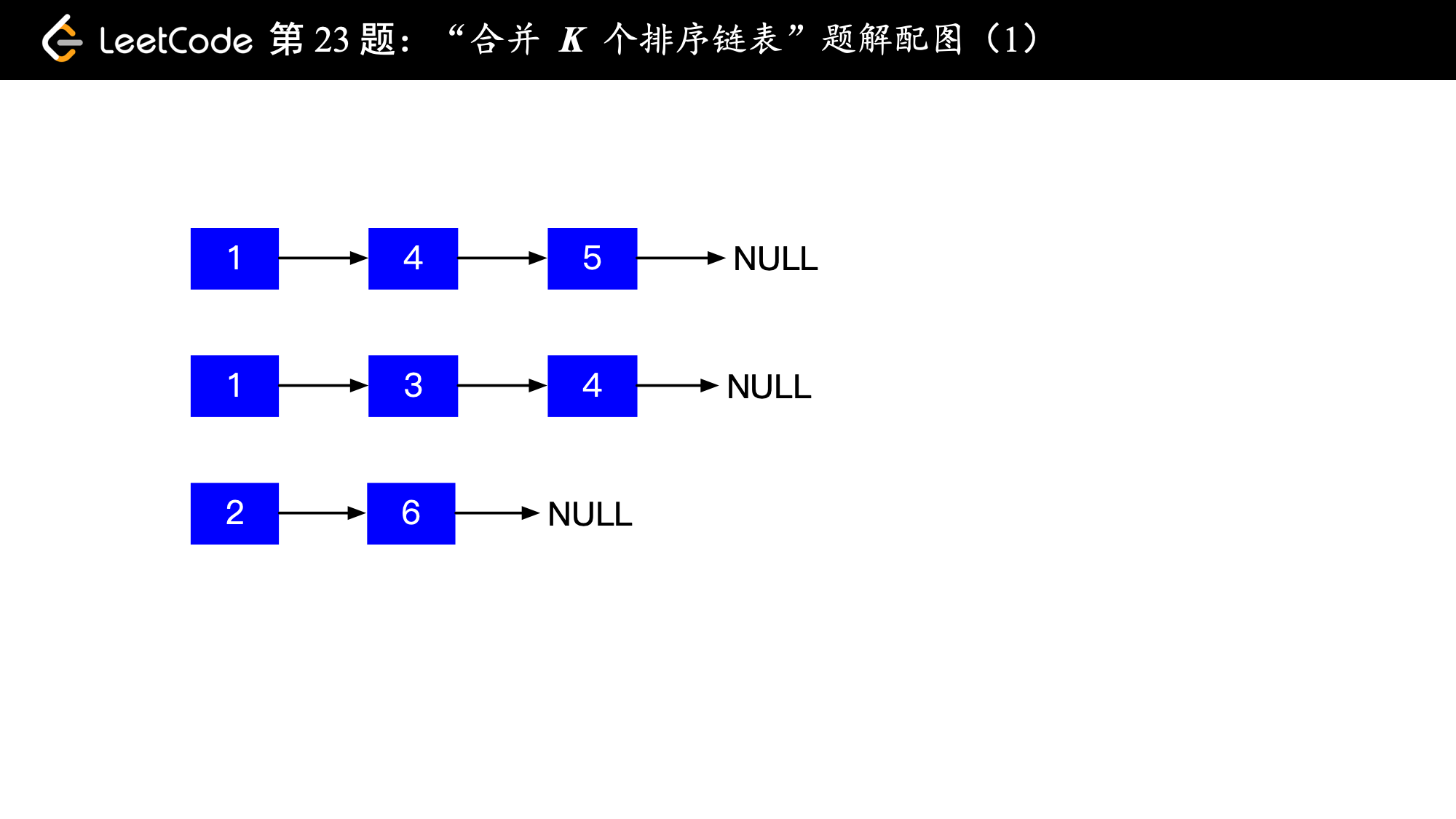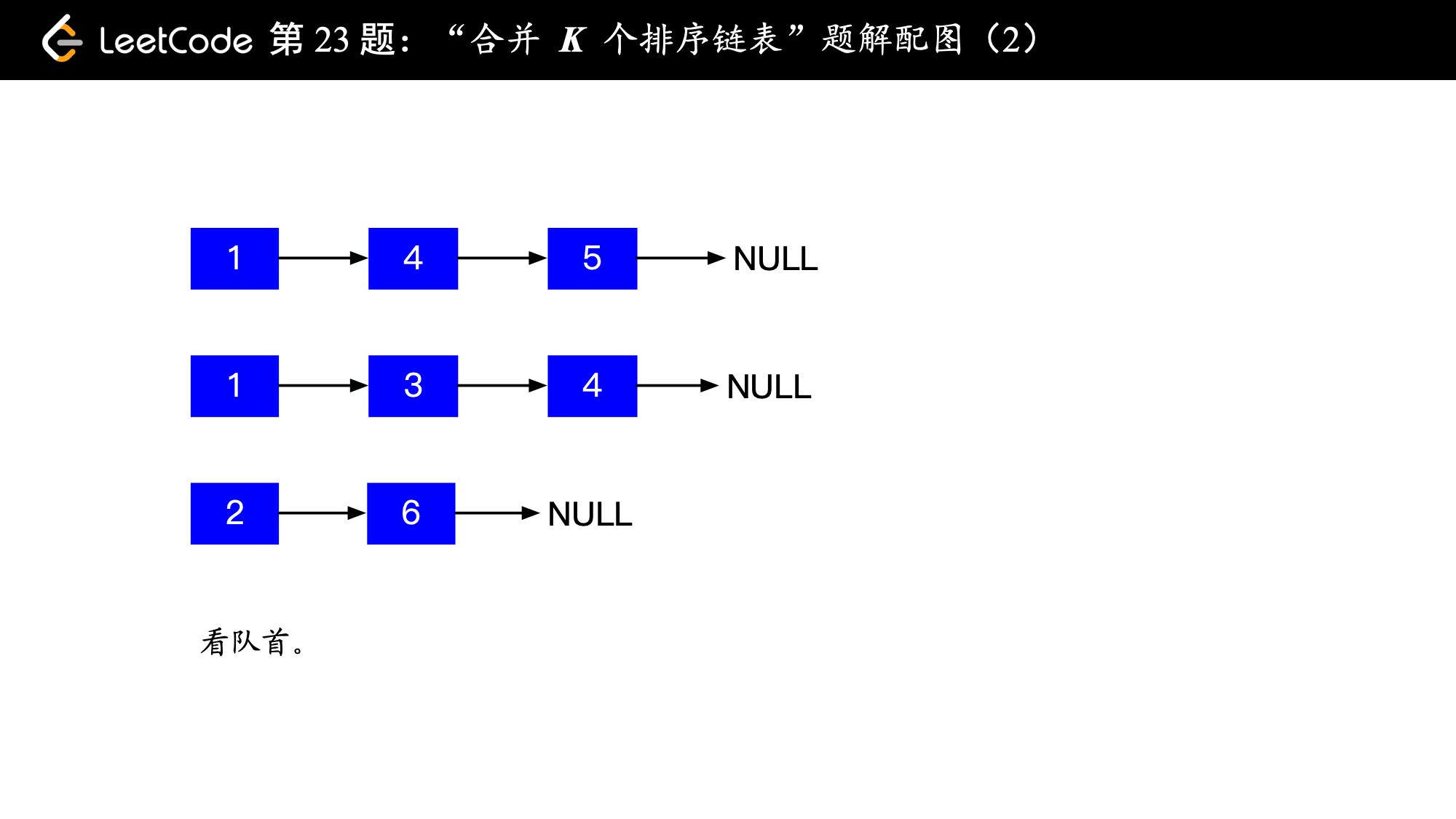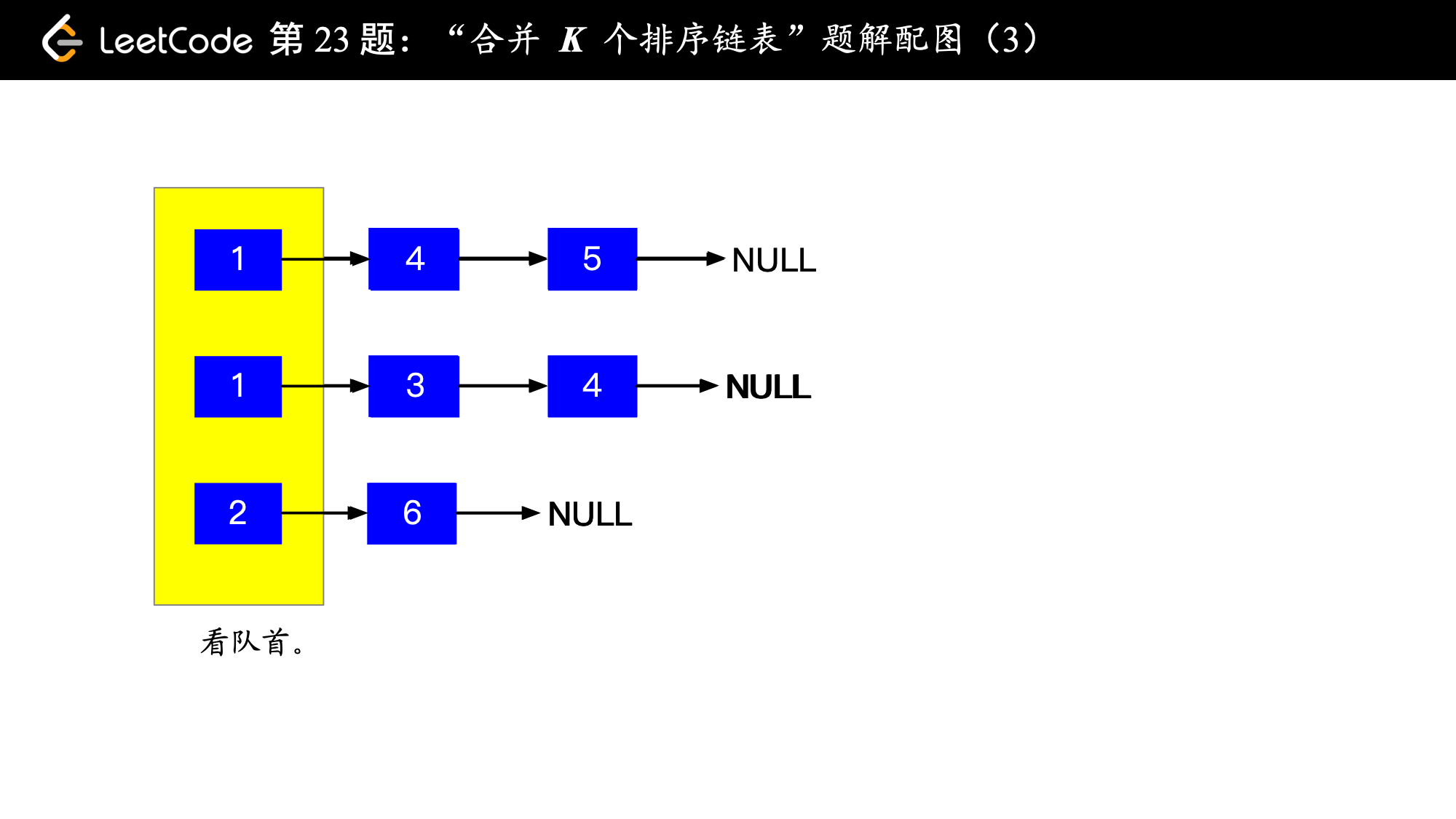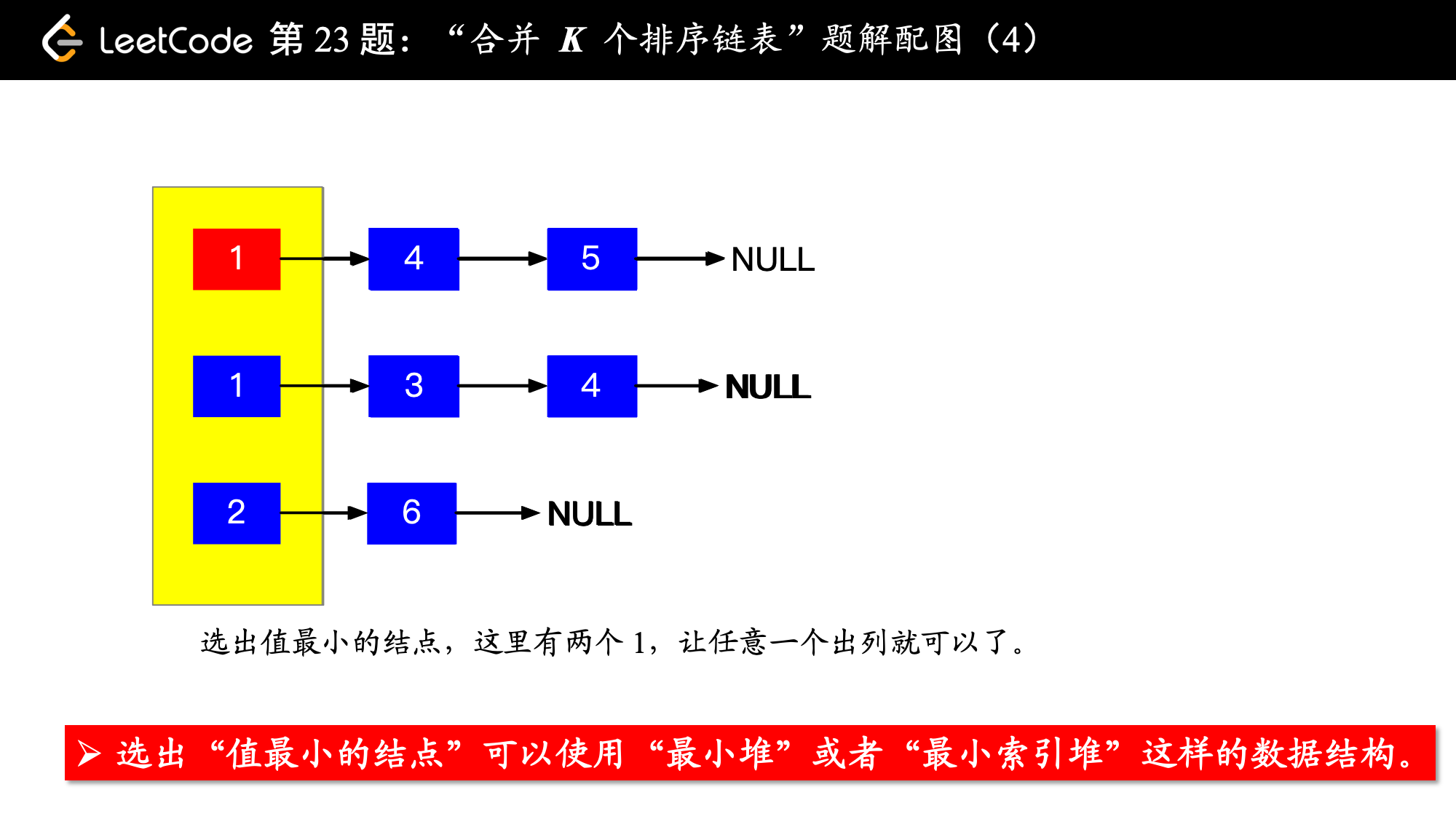Python3 代码：Python3 的 heapq 模块传入的 tuple 对象里面不能有引用对象，就只好传一个索引进去了。
Java 代码：保留了一些调试代码。

说明：下面的选项卡中，第 1 个 Python 代码是在 Python3 下提交的代码，第 2 个 Python 代码是在 Python2 下提交的代码。

参考代码 1：

Python 代码：

# Python3 下的代码
from typing import List
import heapq

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None


class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        l = []
        size = len(lists)

        for index in range(size):
            # 针对一些特殊的测试用例，有的链表可能是空链表
            if lists[index]:
                heapq.heappush(l, (lists[index].val, index))

        dummy_node = ListNode(-1)
        cur = dummy_node

        while l:
            _, index = heapq.heappop(l)

            # 定位到此时应该出列的那个链表的头结点
            head = lists[index]
            # 开始“穿针引线”
            cur.next = head
            cur = cur.next
            # 同样不要忘记判断到链表末尾结点的时候
            if head.next:
                # 刚刚出列的那个链表的下一个结点成为新的链表头结点加入优先队列
                heapq.heappush(l, (head.next.val, index))
                # 切断刚刚出列的那个链表的头结点引用
                lists[index] = head.next
                head.next = None
        return dummy_node.next

Python 代码：

# Python2 下的代码
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None


class Solution:
    def mergeKLists(self, lists):
        import heapq
        l = []
        for head in lists:
            if head:
                heapq.heappush(l, (head.val, head))
        dummy_node = ListNode(-1)
        cur = dummy_node

        while l:
            _, head = heapq.heappop(l)
            cur.next = head
            cur = cur.next
            if head.next:
                heapq.heappush(l, (head.next.val, head.next))

        return dummy_node.next

Java 代码：

import java.util.Comparator;
import java.util.PriorityQueue;

class ListNode {
    int val;
    ListNode next;

    ListNode(int x) {
        val = x;
    }

    ListNode(Integer[] nums) {
        ListNode currNode = this;
        currNode.val = nums[0];
        for (int i = 1; i < nums.length; i++) {
            currNode.next = new ListNode(nums[i]);
            currNode = currNode.next;
        }
    }

    @Override
    public String toString() {
        ListNode currNode = this;
        StringBuilder s = new StringBuilder();
        while (currNode != null) {
            s.append(currNode.val);
            s.append(" -> ");
            currNode = currNode.next;
        }
        // 最后添加一个 NULL 标志表示添加到末尾了
        s.append("NULL");
        return s.toString();
    }
}

public class Solution {

    public ListNode mergeKLists(ListNode[] lists) {
        int len = lists.length;
        if (len == 0) {
            return null;
        }
        PriorityQueue<ListNode> priorityQueue = new PriorityQueue<>(len, Comparator.comparingInt(a -> a.val));
        ListNode dummyNode = new ListNode(-1);
        ListNode curNode = dummyNode;
        for (ListNode list : lists) {
            if (list != null) {
                // 这一步很关键，不能也没有必要将空对象添加到优先队列中
                priorityQueue.add(list);
            }
        }
        while (!priorityQueue.isEmpty()) {
            // 优先队列非空才能出队
            ListNode node = priorityQueue.poll();
            // 当前节点的 next 指针指向出队元素
            curNode.next = node;
            // 当前指针向前移动一个元素，指向了刚刚出队的那个元素
            curNode = curNode.next;
            if (curNode.next != null) {
                // 只有非空节点才能加入到优先队列中
                priorityQueue.add(curNode.next);
            }
        }
        return dummyNode.next;
    }

    public static void main(String[] args) {
        Integer[] nums1 = {1, 4, 5};
        Integer[] nums2 = {1, 3, 4};
        Integer[] nums3 = {2, 6};
        ListNode head1 = new ListNode(nums1);
        ListNode head2 = new ListNode(nums2);
        ListNode head3 = new ListNode(nums3);
        ListNode[] lists = new ListNode[3];
        lists[0] = head1;
        lists[1] = head2;
        lists[2] = head3;
        Solution solution = new Solution();
        ListNode mergeKLists = solution.mergeKLists(lists);
        System.out.println(mergeKLists);
    }
}

在文末附上了使用最小索引堆解决这个问题的代码，稍显复杂，仅供参考。

复杂度分析：

时间复杂度： $O(N \log k)$ ，这里 $N$ 是这 $k$ 个链表的结点总数，每一次从一个优先队列中选出一个最小结点的时间复杂度是 $O(\log k)$ ，故时间复杂度为 $O(N \log k)$ 。
空间复杂度： $O(k)$ ，使用优先队列需要 $k$ 个空间，“穿针引线”需要常数个空间，因此空间复杂度为 $O(k)$ 。

方法二：分治法

根据之前处理链表的经验（例如 LeetCode 第 206 题：反转链表），如果我们不想“穿针引线”，那么“递归”、“分治”是一个不错的选择。

代码结构和“归并排序”可以说是同出一辙：

1、先一分为二，分别“递归地”解决了与原问题同结构，但规模更小的两个子问题；

2、再考虑如何合并，这个合并的过程也是一个递归方法（同 LeetCode 第 21 题：合并两个有序链表）。

参考代码 2：

Python 代码：

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None


class Solution:
    def mergeKLists(self, lists):
        size = len(lists)
        if size == 0:
            return None
        return self.__merge_k_lists(lists, 0, size - 1)

    def __merge_k_lists(self, lists, left, right):
        if left >= right:
            return lists[left]
        mid = left + (right - left) // 2
        listnode1 = self.__merge_k_lists(lists, left, mid)
        listnode2 = self.__merge_k_lists(lists, mid + 1, right)
        return self.__merge_two_sorted_list_node(listnode1, listnode2)

    def __merge_two_sorted_list_node(self, list1, list2):
        if list1 is None:
            return list2
        if list2 is None:
            return list1

        if list1.val < list2.val:
            list1.next = self.__merge_two_sorted_list_node(list1.next, list2)
            return list1
        else:
            list2.next = self.__merge_two_sorted_list_node(list1, list2.next)
            return list2

Java 代码：

import java.util.Comparator;
import java.util.PriorityQueue;

class ListNode {
    int val;
    ListNode next;

    ListNode(int x) {
        val = x;
    }

    ListNode(Integer[] nums) {
        ListNode currNode = this;
        currNode.val = nums[0];
        for (int i = 1; i < nums.length; i++) {
            currNode.next = new ListNode(nums[i]);
            currNode = currNode.next;
        }
    }

    @Override
    public String toString() {
        ListNode currNode = this;
        StringBuilder s = new StringBuilder();
        while (currNode != null) {
            s.append(currNode.val);
            s.append(" -> ");
            currNode = currNode.next;
        }
        // 最后添加一个 NULL 标志表示添加到末尾了
        s.append("NULL");
        return s.toString();
    }
}

public class Solution {

    public ListNode mergeKLists(ListNode[] lists) {
        int len = lists.length;
        if (len == 0) {
            return null;
        }
        return mergeKLists(lists, 0, len - 1);
    }

    public ListNode mergeKLists(ListNode[] lists, int l, int r) {
        // 思考这里为什么取等于？这是因为根据下文对 mergeKLists 的递归调用情况，区间最窄的时候，只可能是左右端点重合
        if (l == r) {
            return lists[l];
        }
        int mid = (r - l) / 2 + l;
        ListNode l1 = mergeKLists(lists, l, mid);
        ListNode l2 = mergeKLists(lists, mid + 1, r);
        return mergeTwoSortedListNode(l1, l2);
    }

    private ListNode mergeTwoSortedListNode(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        }
        if (l2 == null) {
            return l1;
        }
        if (l1.val < l2.val) {
            l1.next = mergeTwoSortedListNode(l1.next, l2);
            return l1;
        }
        l2.next = mergeTwoSortedListNode(l1, l2.next);
        return l2;
    }
}

复杂度分析：

时间复杂度： $O(N \log k)$ ，这里 $N$ 是这 $k$ 个链表的结点总数， $k$ 个链表二分是对数级别的。
空间复杂度： $O(1)$ ，合并两个排序链表需要“穿针引线”的指针数为常数。

附：方法一的补充：使用最小索引堆

下面使用自己编写最小索引堆完成，代码比较长，仅供参考。

参考代码：

Python 代码：

class IndexMinHeap:

    def __init__(self, capacity):
        self.data = [0 for _ in range(capacity + 1)]
        self.indexes = [0 for _ in range(capacity + 1)]
        self.reverse = [0 for _ in range(capacity + 1)]

        self.count = 0
        self.capacity = capacity

    def size(self):
        return self.count

    def is_empty(self):
        return self.count == 0

    # 此时 insert 要给一个索引位置
    def insert(self, i, item):
        if self.count + 1 > self.capacity:
            raise Exception('堆的容量不够了')

        i += 1
        self.data[i] = item

        self.indexes[self.count + 1] = i
        # 注意：反向查找表是如何更新的
        self.reverse[i] = self.count + 1

        self.count += 1
        self.__shift_up(self.count)

    def __shift_up(self, k):
        while k > 1 and self.data[self.indexes[k // 2]] > self.data[self.indexes[k]]:
            self.indexes[k // 2], self.indexes[k] = self.indexes[k], self.indexes[k // 2]
            # 只要索引发生交换，反向查找表也要更新
            self.reverse[self.indexes[k // 2]] = k // 2
            self.reverse[self.indexes[k]] = k

            k //= 2

    def extract_min(self):
        if self.count == 0:
            raise Exception('堆里没有可以取出的元素')
        # 里面套一层 indexes
        ret = self.data[self.indexes[1]]
        # 交换的是索引
        self.indexes[1], self.indexes[self.count] = self.indexes[self.count], self.indexes[1]
        # 只要索引发生交换，反向查找表也要更新
        self.reverse[self.indexes[1]] = 1
        self.reverse[self.indexes[self.count]] = self.count

        # 设置失效
        self.reverse[self.indexes[self.count]] = 0

        self.count -= 1
        self.__shift_down(1)
        return ret

    def __shift_down(self, k):
        while 2 * k <= self.count:
            j = 2 * k
            # 比较的是 data ，交换的是 indexes
            if j + 1 <= self.count and self.data[self.indexes[j + 1]] < self.data[self.indexes[j]]:
                j = j + 1
            if self.data[self.indexes[k]] <= self.data[self.indexes[j]]:
                break
            self.indexes[k], self.indexes[j] = self.indexes[j], self.indexes[k]

            # 只要索引发生交换，反向查找表也要更新
            self.reverse[self.indexes[k]] = k
            self.reverse[self.indexes[j]] = j

            k = j

    # 新增方法
    def extract_min_index(self):
        assert self.count > 0
        # 减 1 是为了符合用户视角
        ret = self.indexes[1] - 1
        self.indexes[1], self.indexes[self.count] = self.indexes[self.count], self.indexes[1]

        # 只要索引发生交换，反向查找表也要更新
        self.reverse[self.indexes[1]] = 1
        self.reverse[self.indexes[self.count]] = self.count

        # 设置失效
        self.reverse[self.indexes[self.count]] = 0

        self.count -= 1
        self.__shift_down(1)
        return ret

    # 新增方法
    def get_min_index(self):
        return self.indexes[1] - 1

    # 新增方法
    def get_item(self, i):
        # 内部数组的索引比用户视角多 1
        return self.data[i + 1]

    # 新增方法
    def change(self, i, new_item):
        # 把用户视角改成内部索引
        i += 1
        self.data[i] = new_item

        # 重点：下面这一步是找原来数组中索引是 i 的元素
        # 在索引数组中的索引是几，这是一个唯一值，找到即返回
        # 优化：可以引入反向查找技术优化
        j = self.reverse[i]

        self.__shift_down(j)
        self.__shift_up(j)


# Definition for singly-linked list.
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None


class Solution:
    def mergeKLists(self, lists: 'List[ListNode]') -> 'ListNode':

        # 这一步是去掉空链表
        new_lists = []
        for i in range(len(lists)):
            if lists[i]:
                new_lists.append(lists[i])

        size = len(new_lists)
        index_min_heap = IndexMinHeap(size)
        for i in range(size):
            index_min_heap.insert(i,new_lists[i].val)

        dummy = ListNode(-1)
        cur = dummy
        while index_min_heap.size() > 0:
            index = index_min_heap.get_min_index()

            print(index, index_min_heap.data,new_lists[index].val)
            cur.next = ListNode(new_lists[index].val)
            cur = cur.next
            if new_lists[index].next is None:
                # 如果后面没有元素，就可以删掉了
                index_min_heap.extract_min_index()
            else:
                index_min_heap.change(index, new_lists[index].next.val)
                new_lists[index] = new_lists[index].next
        return dummy.next


def create_linked_list(nums):
    if len(nums) == 0:
        return None
    head = ListNode(nums[0])
    cur = head
    for i in range(1, len(nums)):
        cur.next = ListNode(nums[i])
        cur = cur.next
    return head


def print_linked_list(list_node):
    if list_node is None:
        return

    cur = list_node
    while cur:
        print(cur.val, '->', end=' ')
        cur = cur.next
    print('null')


if __name__ == '__main__':
    sorted_linked1 = create_linked_list([i for i in range(1, 20, 3)])
    sorted_linked2 = create_linked_list([i for i in range(2, 20, 3)])
    sorted_linked3 = create_linked_list([i for i in range(3, 20, 3)])

    print_linked_list(sorted_linked1)
    print_linked_list(sorted_linked2)
    print_linked_list(sorted_linked3)

    solution = Solution()

    result = solution.mergeKLists(lists=[sorted_linked1, sorted_linked2, sorted_linked3])
    print_linked_list(result)

    sorted_linked1 = create_linked_list([1,2,3])
    sorted_linked2 = create_linked_list([4,5,6,7])
    sorted_linked3 = create_linked_list([])

    solution = Solution()

    result = solution.mergeKLists(lists=[sorted_linked1, sorted_linked2,sorted_linked3])
    print_linked_list(result)

← LeetCode 第 12 题：“整数转罗马数字”题解 LeetCode 第 310 题：“最小高度树”题解 →

# LeetCode 第 23 题：“合并 K 个排序链表”题解

# 贪心算法、优先队列 + 分治法（Python 代码、Java 代码）

# 方法一：贪心算法、优先队列

# 方法二：分治法

# 附：方法一的补充：使用最小索引堆

LeetCode 第 23 题：“合并 K 个排序链表”题解

贪心算法、优先队列 + 分治法（Python 代码、Java 代码）

方法一：贪心算法、优先队列

方法二：分治法

附：方法一的补充：使用最小索引堆