LeetCode 第 310 题:“最小高度树”题解
题解地址:贪心法:根据拓扑排序的思路(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:310. 最小高度树。
对于一个具有树特征的无向图,我们可选择任何一个节点作为根。图因此可以成为树,在所有可能的树中,具有最小高度的树被称为最小高度树。给出这样的一个图,写出一个函数找到所有的最小高度树并返回他们的根节点。
格式
该图包含 n 个节点,标记为 0 到 n - 1。给定数字 n 和一个无向边 edges 列表(每一个边都是一对标签)。
你可以假设没有重复的边会出现在 edges 中。由于所有的边都是无向边, [0, 1]和 [1, 0] 是相同的,因此不会同时出现在 edges 里。
示例 1:
输入: n = 4, edges = [[1, 0], [1, 2], [1, 3]]
0 | 1 / \ 2 3输出: [1] 示例 2:
输入: n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]]
0 1 2 \ | / 3 | 4 | 5输出: [3, 4] 说明:
根据树的定义,树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。 树的高度是指根节点和叶子节点之间最长向下路径上边的数量。
贪心法:根据拓扑排序的思路(Python 代码、Java 代码)
思路分析:
这道题一开始给我的感觉特别像拓扑排序,做下来,感觉它们的本质是一样的,更深层次的思想是贪心算法。
直觉上,一棵树越靠“外面”的结点,我们越不可能把它作为根结点,如果这样做的话,可能树的高度是很高的,例如下面这张图。
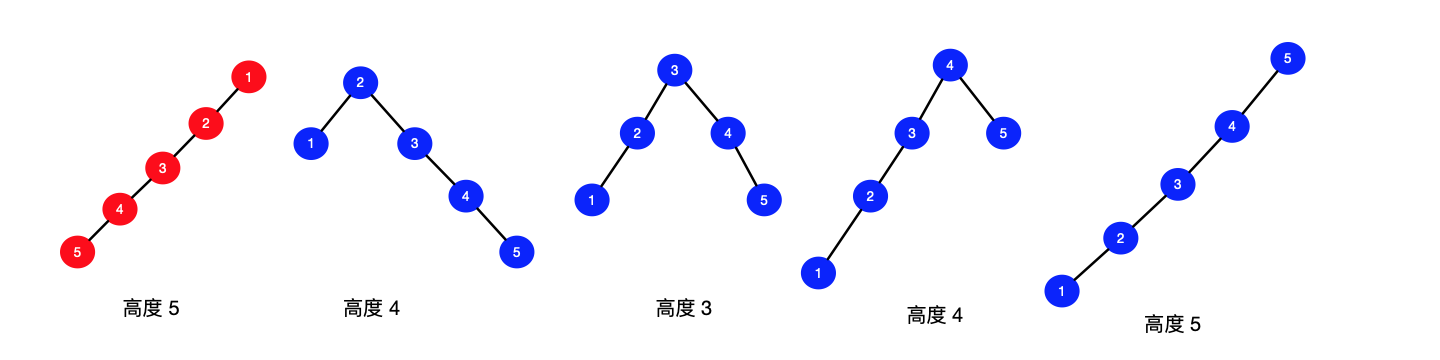
因此,我们使用“剔除边缘结点”的策略,这里的边缘结点就是指连接其它结点最少的结点,用专业的名词来说,就是指向它的结点最少的结点,“入度”最少的结点,为此,我们可以画几张图看一下。
(下面这这张图,我画得很潦草,我不想说清楚画这张图表示的意思,而是想说,有的时候分析问题,需要自己动手,比看别人的思路的理解要深刻。)
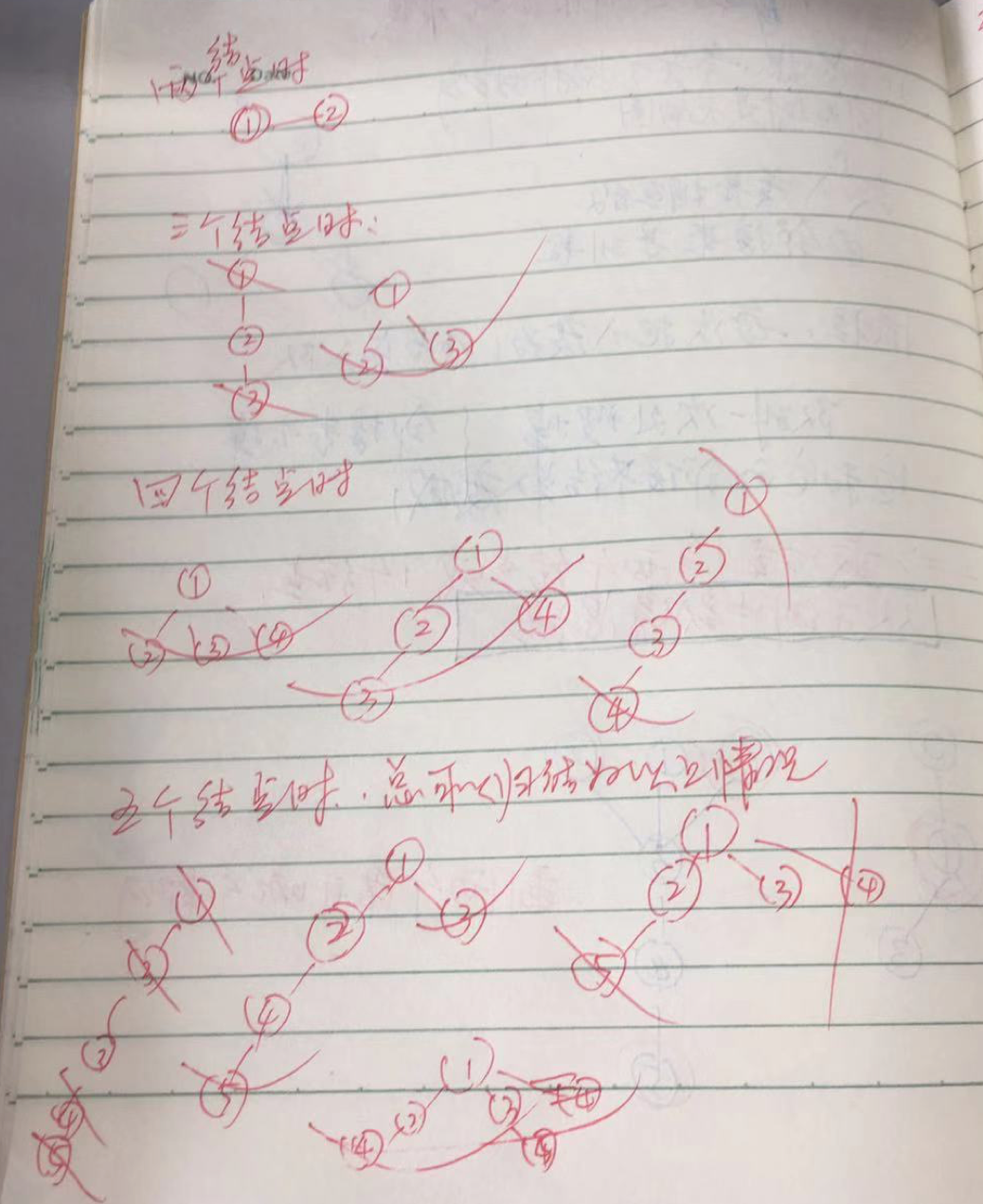
画完这张图,我们能归纳出,结点最后只会剩下 1 个或者 2 个。如果对这个结论还不确定的朋友,不妨多画几张图,把结点个数为 6 个 、7 个时候的情况也考虑一下。
综上所述,总结一下我们的算法:每次总是删除“入度”个数最少的结点,因为树是无向无环图,删除了它们以后,与之相连的结点的入度也相应地减少 1,直到最后剩下 1 个结点或者 2 个结点。
在编码的时候,我借鉴了“拓扑排序”的代码,使用了“邻接表”表示图,使用了“入度数组”,还使用了队列保存了下一轮要“剔除”的结点编号。关于拓扑排序的知识和代码实现,可以参考「力扣」第 207 题:课程表 和「力扣」第 210 题:课程表 II。
参考代码:
Python 代码:
class Solution:
# 贪心法
def findMinHeightTrees(self, n, edges):
if n <= 2:
return [i for i in range(n)]
from collections import defaultdict
from collections import deque
in_degrees = [0] * n
# True 表示保留,如果设置为 False 则表示删除
res = [True] * n
# 邻接表
adjs = defaultdict(list)
for edge in edges:
in_degrees[edge[0]] += 1
in_degrees[edge[1]] += 1
adjs[edge[0]].append(edge[1])
adjs[edge[1]].append(edge[0])
deque = deque()
for i in range(n):
if in_degrees[i] == 1:
deque.append(i)
# 根据示例,可知,最后可能剩下 1 个结点或者 2 个结点
# 或者自己画一个图也能分析出来
while n > 2:
size = len(deque)
# 一次减去当前队列这么多个结点
n -= size
for i in range(size):
top = deque.popleft()
res[top] = False
successors = adjs[top]
# 它和它的邻接点的入度全部减 1
successors.append(top)
for item in successors:
# 一个结点的入度重复减是没有关系的
# 我们只关心在最边界的那个结点,把它移除,所以可以认为是贪心法
in_degrees[item] -= 1
if in_degrees[item] == 1:
deque.append(item)
return [i for i in range(len(res)) if res[i]]
Java 代码:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Set;
public class Solution {
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
List<Integer> res = new ArrayList<>();
// 特判
if (n <= 2) {
for (int i = 0; i < n; i++) {
res.add(i);
}
return res;
}
// 入度数组,每一次要把入度为 1 的结点剔除
int[] inDegrees = new int[n];
// 默认为 False,如果剔除,设置为 True
boolean[] result = new boolean[n];
// 因为是无向图,所以邻接表拿出一条边,两个结点都要存一下
// 注意:右边就不要写具体的实现类了,等到实例化的时候再写具体的实现类
Set<Integer>[] adjs = new Set[n];
// 初始化
for (int i = 0; i < n; i++) {
adjs[i] = new HashSet<>();
}
for (int[] edge : edges) {
int start = edge[0];
int end = edge[1];
adjs[start].add(end);
adjs[end].add(start);
inDegrees[start] += 1;
inDegrees[end] += 1;
}
LinkedList<Integer> queue = new LinkedList<>();
// 入度为 1 的结点入队
for (int i = 0; i < n; i++) {
if (inDegrees[i] == 1) {
queue.addLast(i);
}
}
// 注意边界条件 n == 2 和 n == 1 是如何分析出来的
while (n > 2) {
int size = queue.size();
System.out.println(queue);
// 一次减去这么多
n -= size;
for (int i = 0; i < size; i++) {
int top = queue.removeFirst();
result[top] = true;
inDegrees[top] -= 1;
// 把它和它的邻接结点的入度全部减 1
Set<Integer> successors = adjs[top];
for (Integer successor : successors) {
inDegrees[successor] -= 1;
if (inDegrees[successor] == 1) {
queue.addLast(successor);
}
}
}
}
n = result.length;
for (int i = 0; i < n; i++) {
if (!result[i]) {
res.add(i);
}
}
return res;
}
public static void main(String[] args) {
int[][] edges = new int[][]{{1, 0}, {1, 2}, {1, 3}};
int n = 4;
Solution solution = new Solution();
List<Integer> res = solution.findMinHeightTrees(n, edges);
System.out.println(res);
}
}