LeetCode 第 452 题:“用最少数量的箭引爆气球”题解
题解地址:贪心算法(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:452. 用最少数量的箭引爆气球。
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以y坐标并不重要,因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在104个气球。
一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
Example:
输入: [[10,16], [2,8], [1,6], [7,12]]
输出: 2
解释: 对于该样例,我们可以在x = 6(射爆[2,8],[1,6]两个气球)和 x = 11(射爆另外两个气球)。
贪心算法(Python 代码、Java 代码)
解题关键:画图。
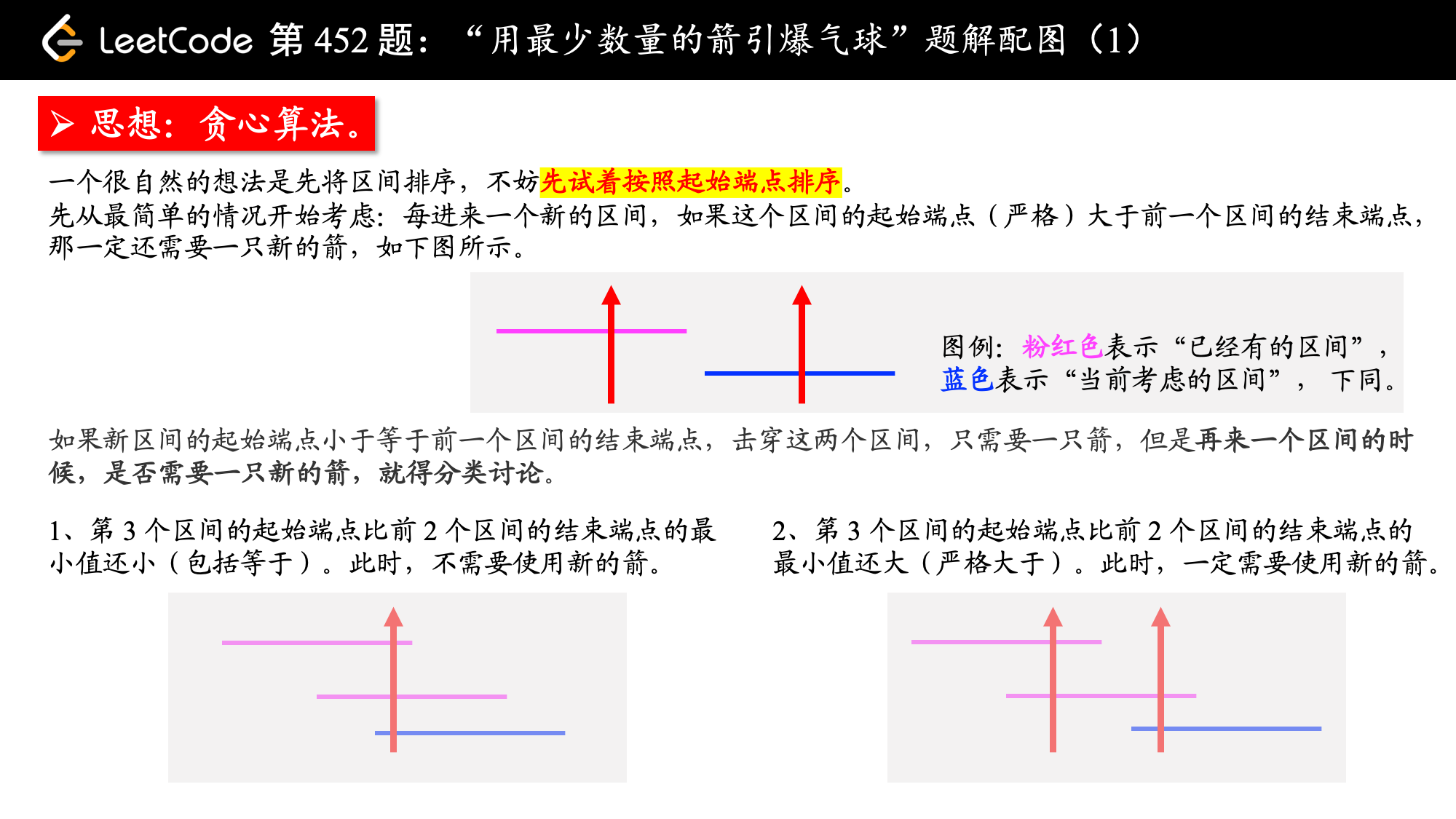
根据以上讨论,我们可以设置一个 end 标记, 它表示:在遍历的过程中使用当前这只箭能够击穿所有气球的最远距离。这个最远距离,在每遍历一个新区间的时候,都会检查一下,取最小值。
根据以上分析,不难写出下面的代码:
参考代码:
Python 代码:
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
size = len(points)
# 特判
if size < 2:
return size
# 按照区间的起始端点排序
points.sort(key=lambda x:x[0])
# 只要有区间就至少需要一只箭
res = 1
# 最远距离:使用当前这只箭能引爆气球的最远距离
end = points[0][1]
for i in range(1, size):
if points[i][0] > end:
end = points[i][1]
res += 1
else:
end = min(end, points[i][1])
return res
Java 代码:
import java.util.Arrays;
import java.util.Comparator;
public class Solution {
public int findMinArrowShots(int[][] points) {
int plen = points.length;
if (plen < 2) {
return plen;
}
// 按照起点进行排序
Arrays.sort(points, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if (o1[0] != o2[0]) {
return o1[0] - o2[0];
}
return o1[1] - o2[1];
}
});
// 最少的数量
int minCount = 1;
// 第 1 个区间的末尾,目前线段能够达到的最远位置
int end = points[0][1];
// 贪心法,基于上一个箭,记录当前能够射穿的所有的区间
for (int i = 1; i < plen; i++) {
if (points[i][0] <= end) {
end = Math.min(end, points[i][1]);
} else {
minCount++;
end = points[i][1];
}
}
return minCount;
}
}
这一版代码提交就已经可以通过了。我们想一想还能不能写得更好一些。经过上面的分析,我们发现,区间的末尾端点很重要:如果不使用新的箭,新区间末尾端点就要和当前的“最远距离”(含义通过上文可以明白)作一个比较,取最小值。那我不妨就按照区间的末尾端点排序,这样如果不使用新的箭,也不用作比较了,比起上面的代码来说,就少了一个分支。
(如果上面的叙述不好理解的话,可以在草稿纸上多画几条线段,就很清楚了。)
参考代码:
Python 代码:
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
size = len(points)
if size < 2:
return size
# 按照区间的末尾端点排序
points.sort(key=lambda x:x[1])
res = 1
# 最远距离:使用当前这只箭能引爆气球的最远距离
end = points[0][1]
for i in range(1, size):
if points[i][0] > end:
end = points[i][1]
res += 1
return res
Java 代码:
import java.util.Arrays;
import java.util.Comparator;
public class Solution {
public int findMinArrowShots(int[][] points) {
int len = points.length;
if (len < 2) {
return len;
}
// 按照区间终点进行排序
Arrays.sort(points, new Comparator<int[]>() {
@Override
public int compare(int[] point1, int[] point2) {
if (point1[1] != point2[1]) {
return point1[1] - point2[1];
}
return point1[0] - point2[0];
}
});
int count = 1;
int end = points[0][1];
for (int i = 1; i < len; i++) {
if (points[i][0] > end) {
// 就得多用一支箭
end = points[i][1];
count++;
}
}
return count;
}
}
复杂度分析:
- 时间复杂度:: 为气球的个数,时间复杂度为排序算法的时间复杂度,感谢用户 @powerboy6 提供的评论。
- 空间复杂度:。