LeetCode 第 377 题:“组合总和 Ⅳ”题解
题解地址:动态规划(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:377. 组合总和 Ⅳ。
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
nums = [1, 2, 3] target = 4
所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。 进阶: 如果给定的数组中含有负数会怎么样? 问题会产生什么变化? 我们需要在题目中添加什么限制来允许负数的出现?
致谢: 特别感谢 @pbrother 添加此问题并创建所有测试用例。
动态规划(Python 代码、Java 代码)
思路分析:
遇到这一类问题,脑子里能想到的常规思路大概有“搜索”、“动态规划”,因为不用得到具体的组合表示,因此“动态规划”应该、差不多就是求解这道问题的方法。
“动态规划”在本质上其实还是“搜索”,并且是“记忆化搜索”。
- “记忆化搜索”求解问题的方式是“从上至下”的,遇到重复的问题,查“缓存”。
- “动态规划”求解问题的方式是“从下至上”的,正是因为“从下至上”,所以遇到“规模更大”的问题的之后,它之前的那些“规模更小”的问题都已经解决过了。因此,不需要“缓存”机制。
所以,我们还是画树形图分析。
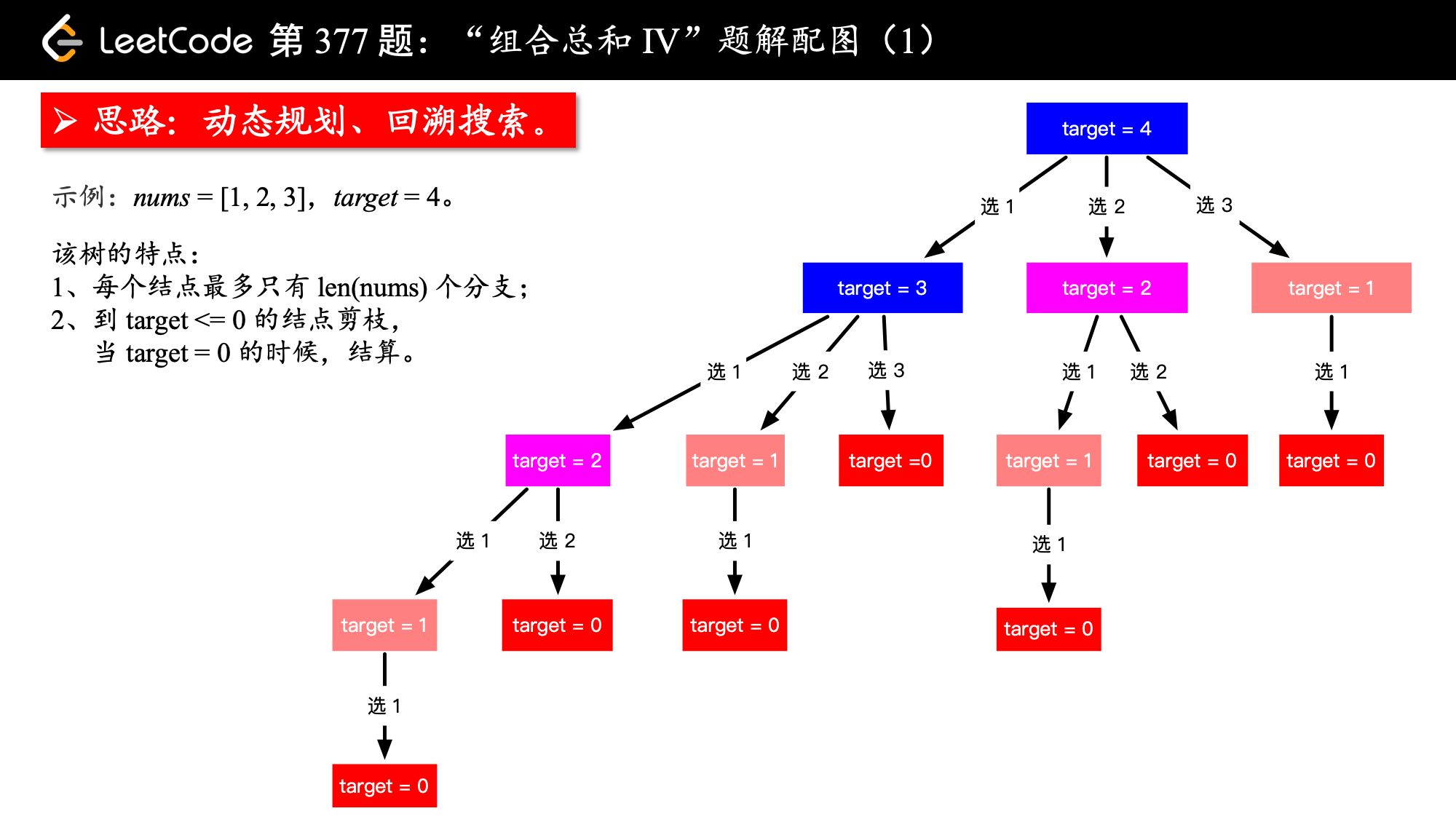
很容易发现“重叠子问题”,因此,我们可以使用“动态规划”来做,如果题目问具体的解,那么用“回溯搜索”做。
对上图的解释:

方法:动态规划
“动态规划”的两个步骤是思考“状态”以及“状态转移方程”。
1、状态
对于“状态”,我们首先思考能不能就用问题当中问的方式定义状态,上面递归树都画出来了。当然就用问题问的方式。
dp[i] :对于给定的由正整数组成且不存在重复数字的数组,和为 i 的组合的个数。
思考输出什么?因为状态就是问题当中问的方式而定义的,因此输出就是最后一个状态 dp[n]。
2、状态转移方程
由上面的树形图,可以很容易地写出状态转移方程:
dp[i] = sum{dp[i - num] for num in nums and if i >= num}
注意:在 这一点,我们定义 dp[0] = 1的,它表示如果 nums 里有一个数恰好等于 target,它单独成为 种可能。
参考代码:
Python 代码:
class Solution:
def combinationSum4(self, nums, target):
size = len(nums)
if size == 0 or target <= 0:
return 0
dp = [0 for _ in range(target + 1)]
# 这一步很关键,想想为什么 dp[0] 是 1
# 因为 0 表示空集,空集和它"前面"的元素凑成一种解法,所以是 1
# 这一步要加深体会
dp[0] = 1
for i in range(1, target + 1):
for j in range(size):
if i >= nums[j]:
dp[i] += dp[i - nums[j]]
return dp[-1]
Java 代码:
public class Solution {
/**
* 这里状态定义就是题目要求的,并不难,状态转移方程要动点脑子,也不难:
* 状态转移方程:dp[i]= dp[i - nums[0]] + dp[i - nums[1]] + dp[i - nums[2]] + ... (当 [] 里面的数 >= 0)
* 特别注意:dp[0] = 1,表示,如果那个硬币的面值刚刚好等于需要凑出的价值,这个就成为 1 种组合方案
* 再举一个具体的例子:nums=[1, 3, 4], target=7;
* dp[7] = dp[6] + dp[4] + dp[3]
* 即:7 的组合数可以由三部分组成,1 和 dp[6],3 和 dp[4], 4 和dp[3];
*
* @param nums
* @param target
* @return
*/
public int combinationSum4(int[] nums, int target) {
int len = nums.length;
if (len == 0) {
return 0;
}
int[] dp = new int[target + 1];
// 注意:理解这一句代码的含义
dp[0] = 1;
for (int i = 1; i <= target; i++) {
for (int j = 0; j < len; j++) {
if (i - nums[j] >= 0) {
dp[i] += dp[i - nums[j]];
}
}
}
return dp[target];
}
public static void main(String[] args) {
int[] nums = {1, 2, 3};
int target = 4;
Solution2 solution2 = new Solution2();
int combinationSum4 = solution2.combinationSum4(nums, target);
System.out.println(combinationSum4);
}
}
对于进阶问题的思考
1、如果给定的数组中含有负数会怎么样?问题会产生什么变化?
如果有负数,相当于给定数组中的元素有了更多的组合,特别是出现了一对相反数的时候,例如题目中的示例 [-4, 1, 2, 3, 4],target = 4 的时候,-4 和 4 可以无限次地、成对添加到题目中的示例中,成为新的组合,那么这道问题就没有什么意义了。
仔细思考,负数我只要不选它就行了。但由于这道问题的问法是“组合”,因此我们要保证有负数参与进来,不能够与已有的正数的组合之和为 0 即可。
2、我们需要在题目中添加什么限制来允许负数的出现?
- 如果有负数参与进来,不能够与已有的正数的组合之和为
0; - 或者限制负数的使用次数,设计成类似 0-1 背包问题的样子。
可能有考虑不完全的地方,欢迎讨论。