LeetCode 第 300 题:“最长上升子序列”题解
题解地址:动态规划 + 贪心算法(二分法)(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:300. 最长上升子序列。
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18] 输出: 4 解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
动态规划 + 贪心算法(二分法)(Python 代码、Java 代码)
最长上升子序列,英文名 Longest Increasing Subsequence,是著名的 LIS 问题。
本文介绍了两种方法解决这个问题,第一种是常规解法:动态规划,时间复杂度为 ,第二种方法有一定技巧性,可以认为是贪心算法 + 二分查找,时间复杂度为 ,这里 表示数组的长度。
审题
首先对题目中“上升”和“子序列”这两个关键字做一些解释,以帮助您更好地理解 LIS 问题。
1、子序列(Subsequence):“子序列”并不要求是连续子序列,只要保证元素前后顺序一致即可,例如:序列 [4, 6, 5] 是 [1, 2, 4, 3, 7, 6, 5] 的一个子序列;
2、上升:这里“上升”要求严格“上升”。
例如一个序列 [2, 3, 3, 6, 7] ,由于 3 重复了,所以不是严格“上升”的,因此它不是题目要求的“上升”序列。
一个序列可能有多个最长上升子序列,题目中只要我们求这个最长的长度。如果使用回溯算法,选择所有的子序列进行判断,时间复杂度为 。
LIS 问题是一个最优化问题,可以考虑使用动态规划完成。
方法一:动态规划
“动态规划”的两个步骤是思考“状态”以及“状态转移方程”。
有的资料又将“动态规划”分为 3 步:
- base case:思考问题规模最小的时候,是什么情况;
- update function:自下而上思考这个问题,即上面的“状态转移方程”;
- gola:重点强调了输出是什么,很多时候输出并不一定是最后一个状态。
我觉得这种分法更细致一点,“状态”以及“状态转移方程”也没有问题,但是我觉得还要加上一个,思考一下“输出”是什么,即将第 2 种的第 3 步加上去,在下面的分析中,我还会强调这一点。
1、定义状态
首先我们考虑能否将题目的问法定义成状态,即 dp[i] 表示长度为 i 的最长上升子序列的长度,但仔细思考之后,我们发现:由于“子序列”不要求连续,长度为 i - 1 的最长上升子序列,与长度为 i 的“最长上升子序列之间的递推关系并不那么容易得到。
但我们由「力扣」第 3 题:“无重复字符的最长子串”以及「力扣」第 53 题:“最大子序和”这两个问题的经验,再结合题意,可以知道,“上升”的递推关系是:看子序列最后一个数,如果一个新数,比子序列最后一个数还大,那么就可以放在这个子序列的最后,形成一个更长的子序列。反正一个子序列一定会以一个数字结尾,那我就将状态成以 nums[i] 结尾的“最长上升子序列”的长度,这一点是常见的。
dp[i]:表示以第 i 个数字为结尾的“最长上升子序列”的长度。即在 [0, ..., i] 的范围内,选择 以数字 nums[i] 结尾 可以获得的最长上升子序列的长度。注意:以第 i 个数字为结尾,即 要求 nums[i] 必须被选取。
初始化的时候,因为每个元素自己可以认为是一个长度为 的子序列,所以可以将 dp 数组的值全部设置为 。
定义输出:下面要考虑一下输出,由于状态不是题目中的问法,因此不能将最后一个状态作为输出,这里输出是把 dp[0]、dp[1]、……、dp[n - 1] 全部看一遍,取最大值。
2、推导“状态转移方程”
遍历到索引是 i 的数的时候,根据上面“状态”的定义,考虑把 i 之前的所有的数都看一遍,只要当前的数 nums[i] 严格大于之前的某个数,那么 nums[i] 就可以接在这个数后面形成一个更长的上升子序列。因此,dp[i] 就是之前严格小于 nums[i] 的“状态”最大值加 。
因此,状态转移方程是:
dp[i] = max{1 + dp[j] for j < i if nums[j] < nums[i]}
看下面的例子或者代码来理解这个状态转移方程。
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
 ,
, ,
, ,
,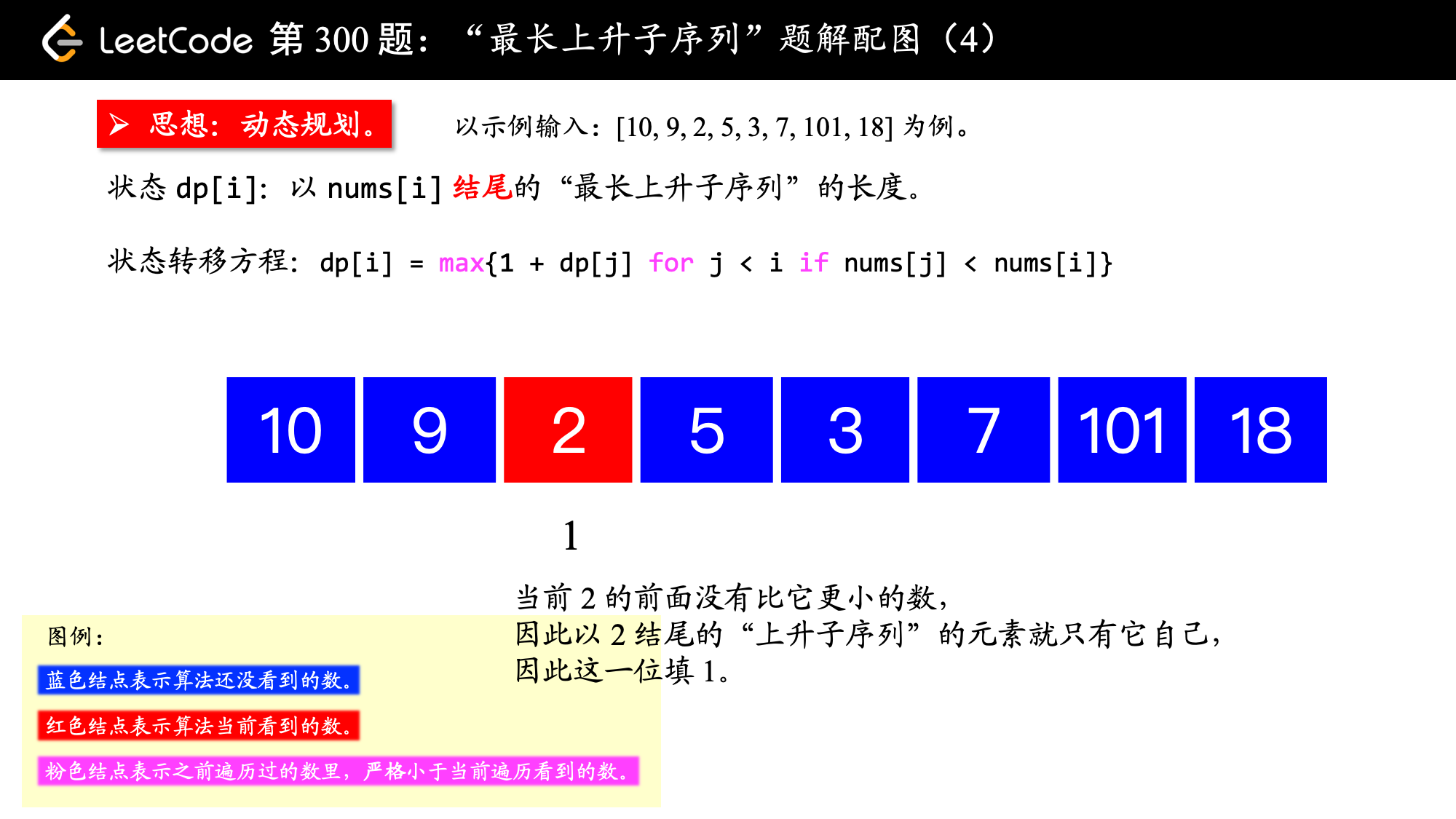 ,
, ,
, ,
, ,
, ,
, ,
,
再看一个例子,熟悉“状态转移”的过程:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
参考代码 1:
Python 代码:
class Solution:
# 将 dp 数组定义为:以 nums[i] 结尾的最长上升子序列的长度
# 那么题目要求的,就是这个 dp 数组中的最大者
# 以数组 [10, 9, 2, 5, 3, 7, 101, 18] 为例
# dp 的值: 1 1 1 2 2 3 4 4
def lengthOfLIS(self, nums):
size = len(nums)
# 特判
if size <= 1:
return size
dp = [1] * size
for i in range(1, size):
for j in range(i):
if nums[i] > nums[j]:
# + 1 的位置不要加错了
dp[i] = max(dp[i], dp[j] + 1)
# 最后要全部一看遍,取最大值
return max(dp)
Python 代码:
import java.util.Arrays;
public class Solution {
//【关键】将 dp 数组定义为:以 nums[i] 结尾的最长上升子序列的长度
// 那么题目要求的,就是这个 dp 数组中的最大者
// 以数组 [10, 9, 2, 5, 3, 7, 101, 18] 为例:
// dp 的值: 1 1 1 2 2 3 4 4
// 注意实现细节。
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if (len == 0) {
return 0;
}
// 状态的定义是:以 i 结尾的最长上升子序列的长度
// 状态转移方程:之前比最后那个数字小的最长上升子序列的长度 + 1
int[] dp = new int[len];
// 如果只有 1 个元素,那么这个元素自己就构成了最长上升子序列,所以设置为 1 是合理的
Arrays.fill(dp, 1);
// 从第 2 个元素开始,逐个写出 dp 数组的元素的值
for (int i = 1; i < len; i++) {
int curVal = nums[i];
// 找出比当前元素小的哪些元素的最小值
for (int j = 0; j < i; j++) {
if (curVal > nums[j]) {
dp[i] = Integer.max(dp[j] + 1, dp[i]);
}
}
}
// 最后要全部走一遍,看最大值
int res = dp[0];
for (int i = 0; i < len; i++) {
res = Integer.max(res, dp[i]);
}
return res;
}
public static void main(String[] args) {
int[] nums = {10, 9, 2, 5, 3, 7, 101, 18};
Solution solution = new Solution();
int lengthOfLIS = solution.lengthOfLIS(nums);
System.out.println(lengthOfLIS);
}
}
复杂度分析:
- 时间复杂度:,因为有两个
for循环,每个for循环的时间复杂度都是线性的。 - 空间复杂度:,要开和数组等长的状态数组,最后要拉通看一遍状态数组的最大值,因此空间复杂度是 。
这道题还有一个时间复杂度为 的解法,把 其中一个 降到 ,就是如下的“贪心算法 + 二分查找”。
方法二:贪心算法 + 二分查找
首先我们介绍算法的基本思想。
算法的基本思想:
如果前面的数越小,后面接上一个随机数,就会有更大的可能性构成一个更长的“上升子序列”。
这个思想并不难理解,我们举例说明:如果前面的数是 ,后面接上一个随机数,能够构成长度为 的“上升子序列”的可能性,就远远大于前面的数是 ,后面接上一个随机数,能够构成长度为 的“上升子序列”的可能性。
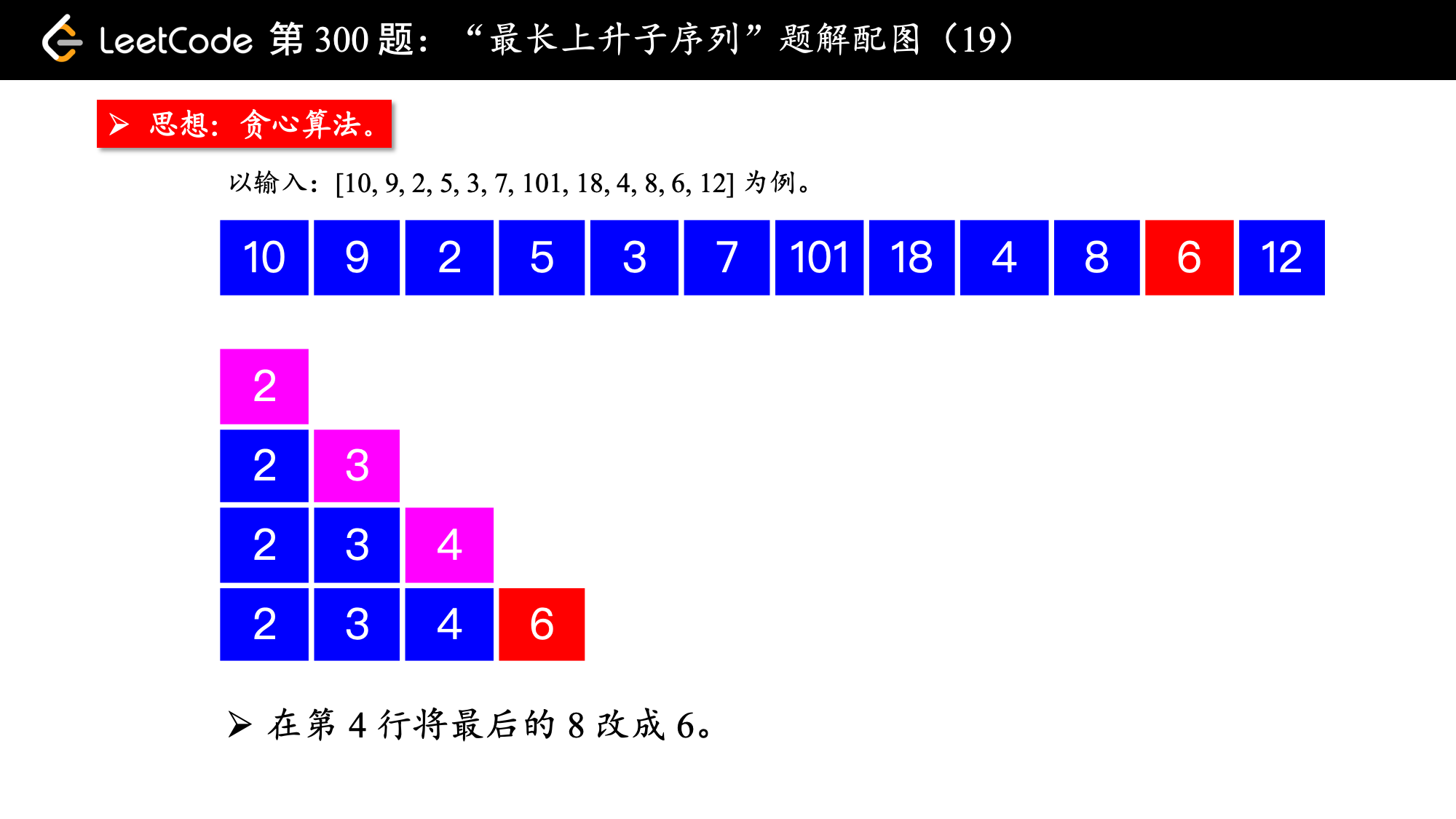
基于这个思想,我们先通过示例介绍算法的流程,然后再做总结,最后把其中关键的地方向大家指出。我在示例的数组后面加上了 4、8、6、12。
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,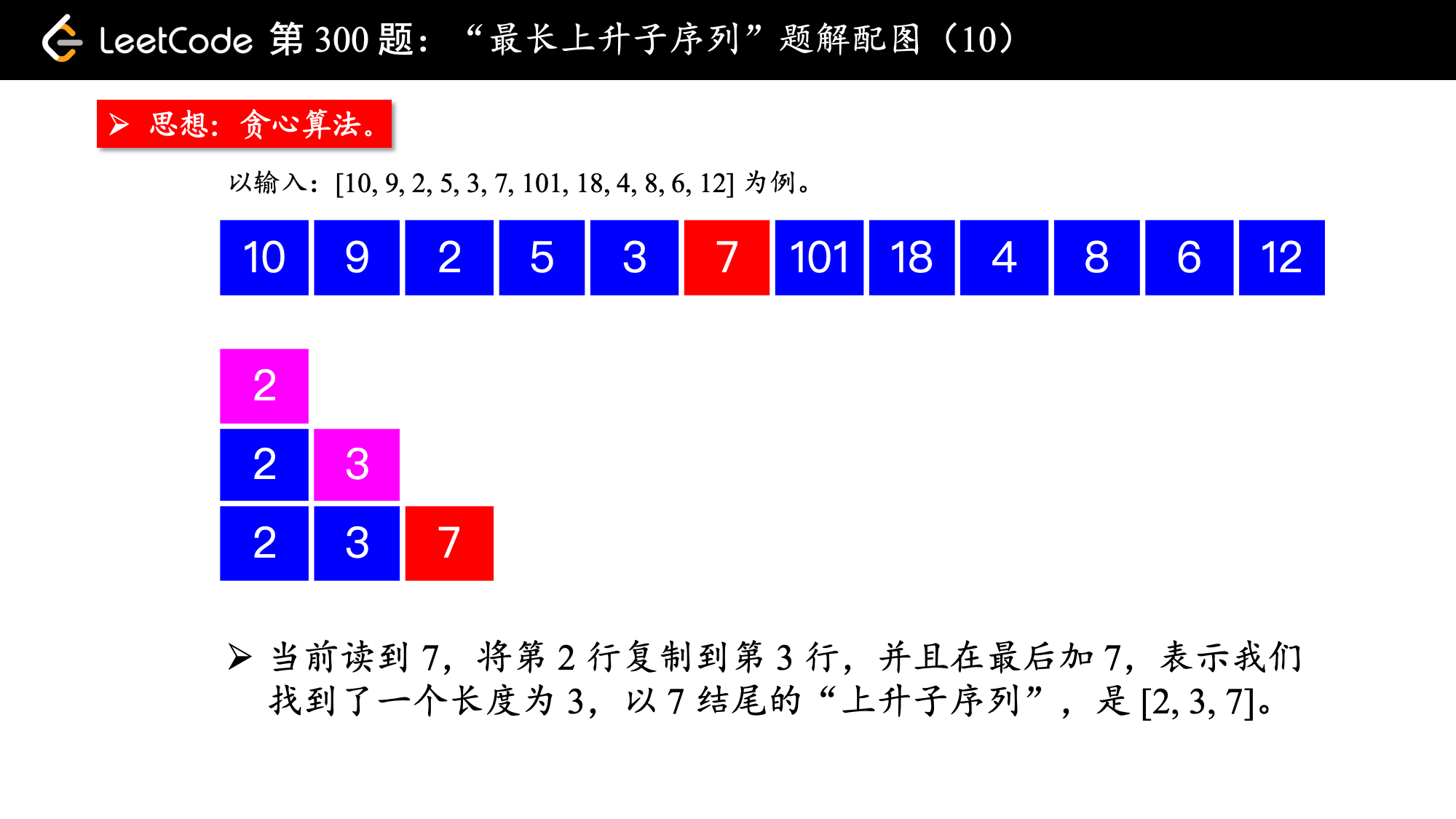 ,
,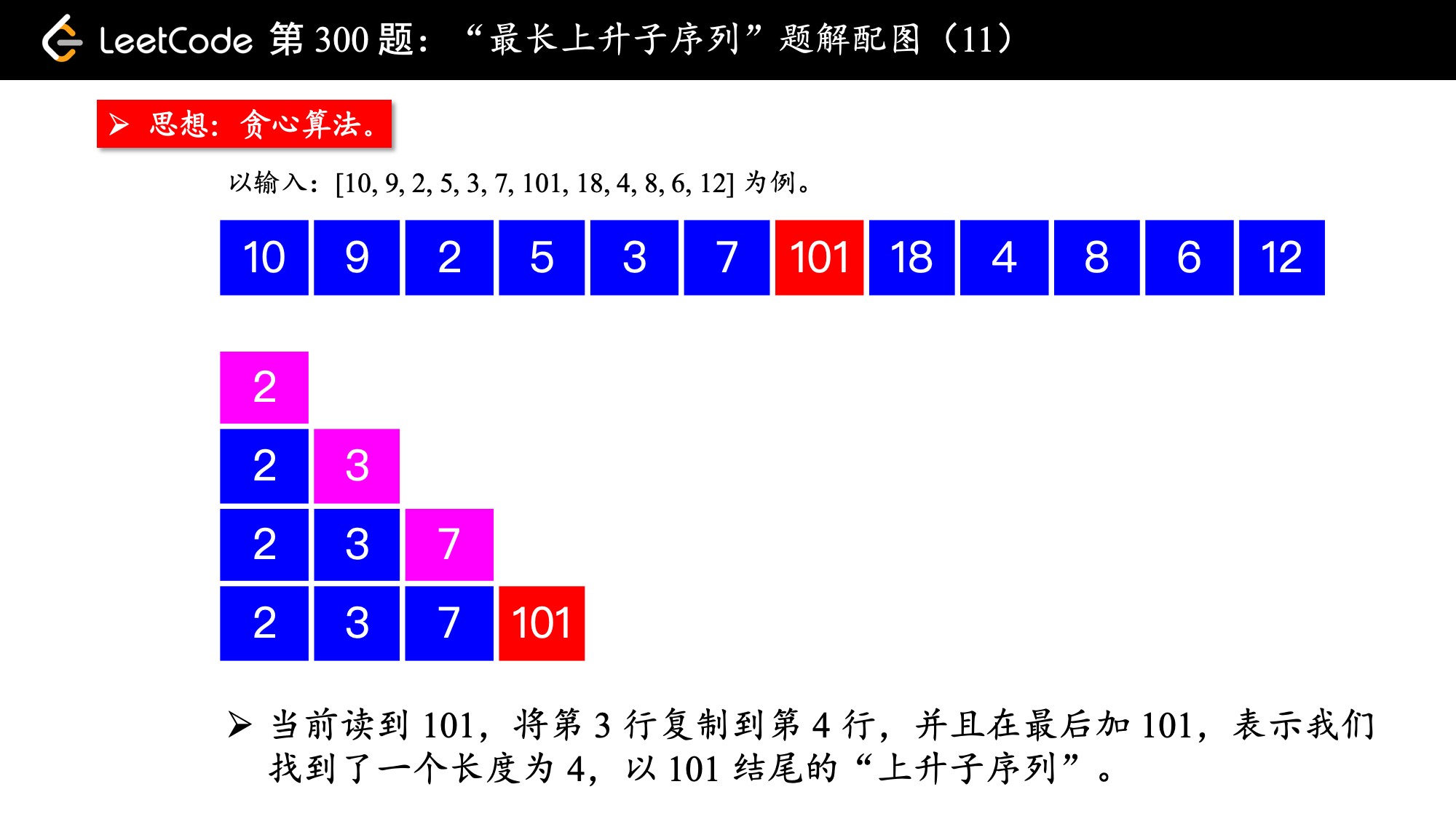 ,
, ,
,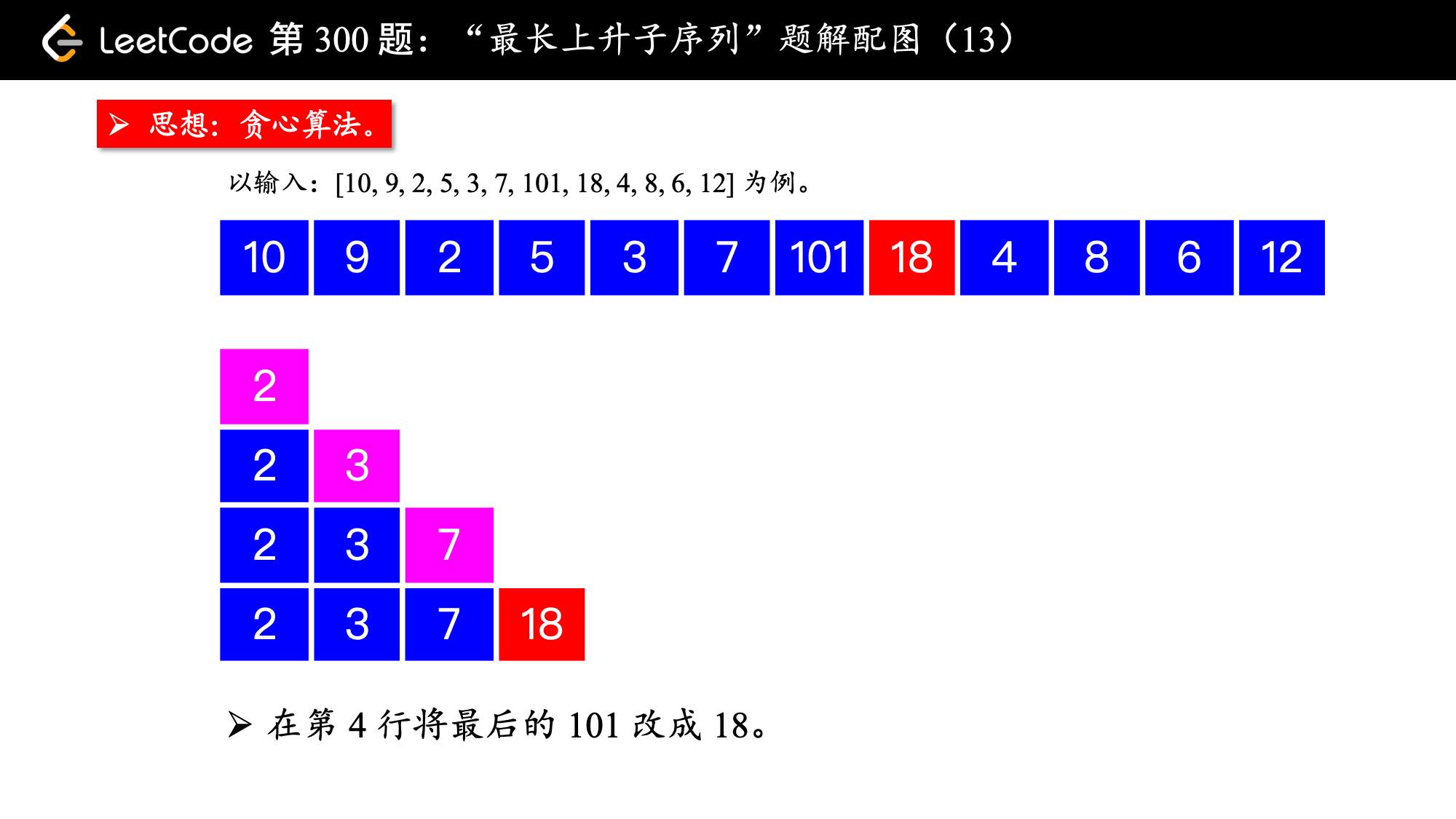 ,
,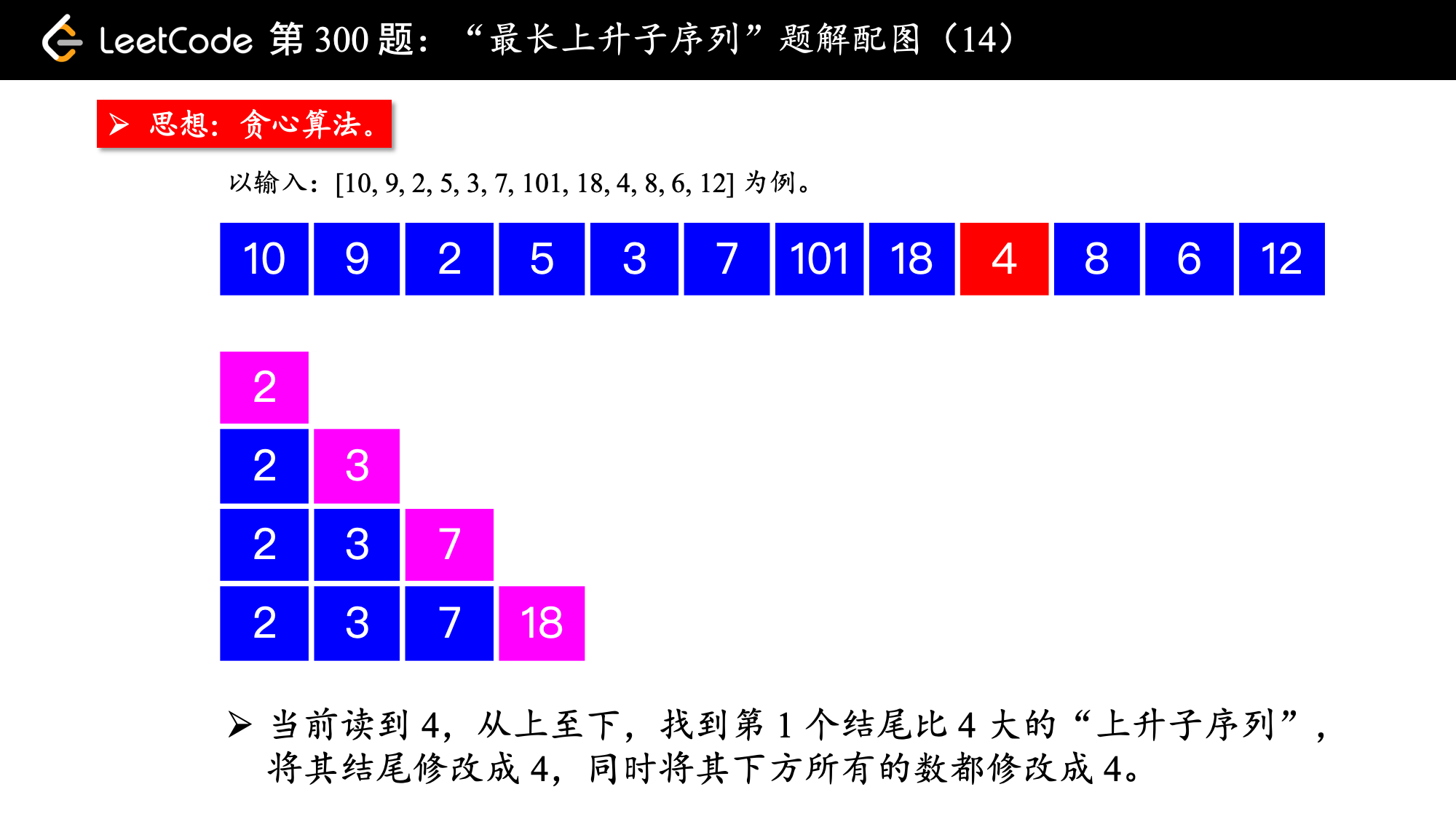 ,
,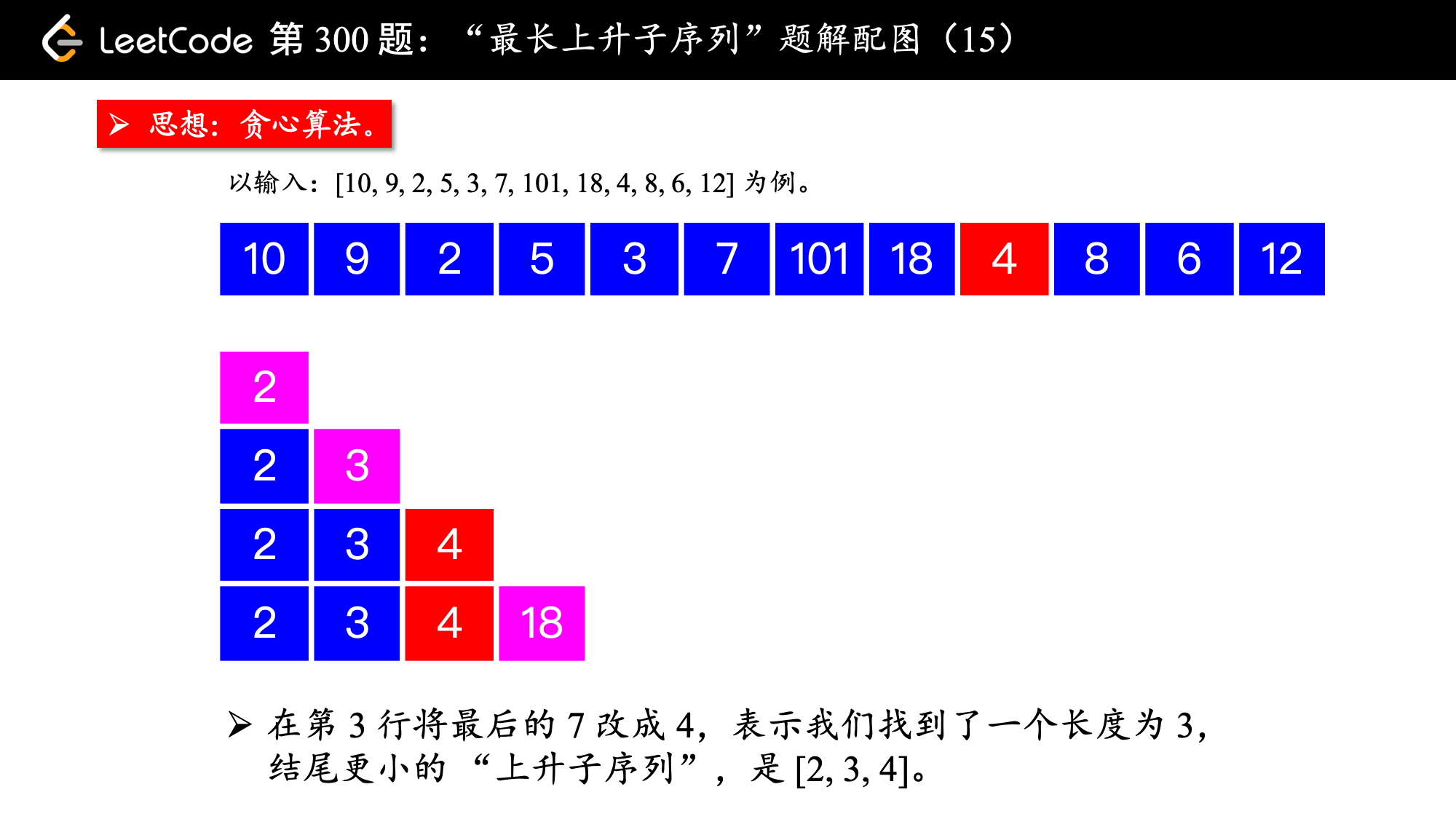 ,
,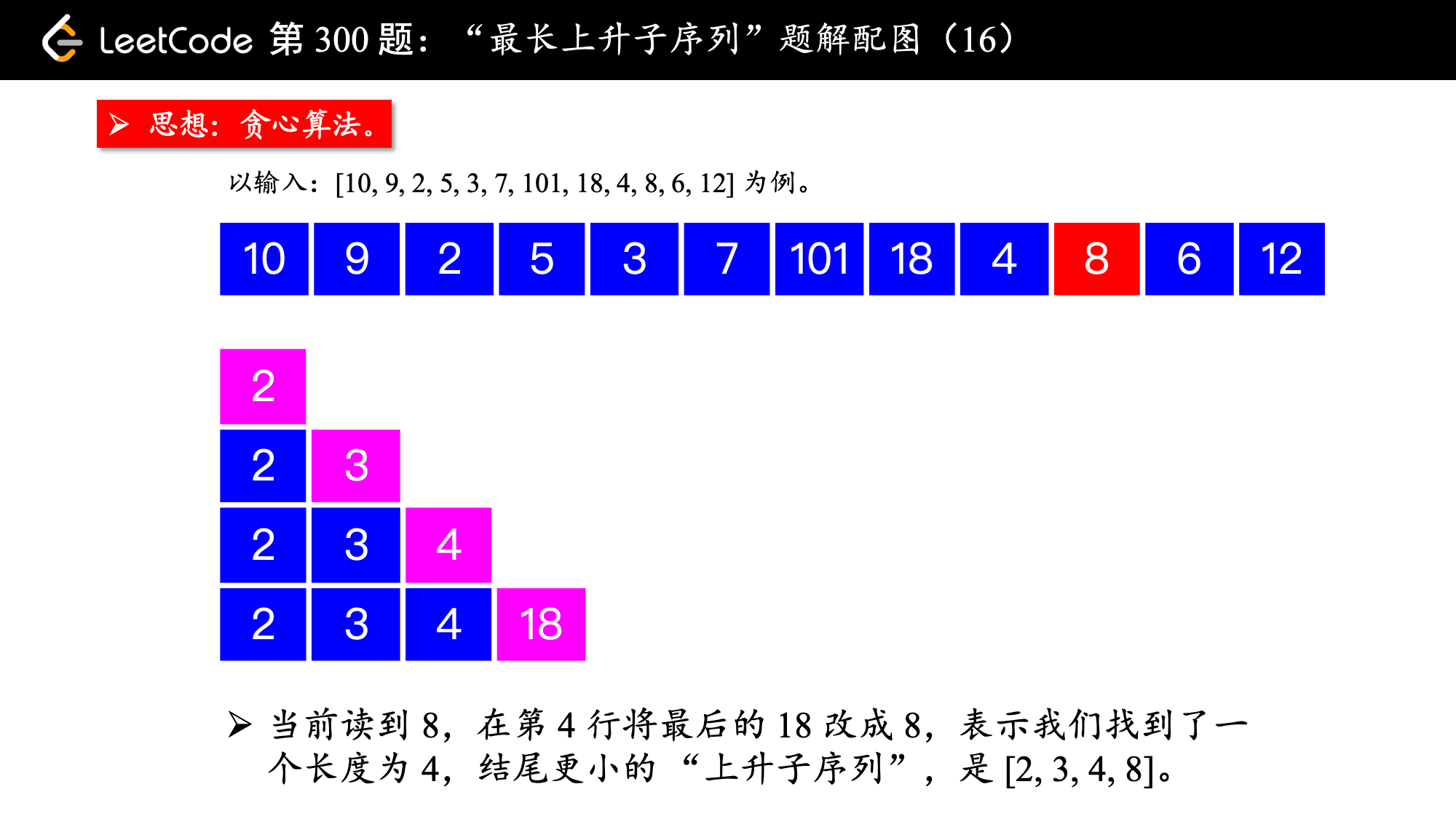 ,
,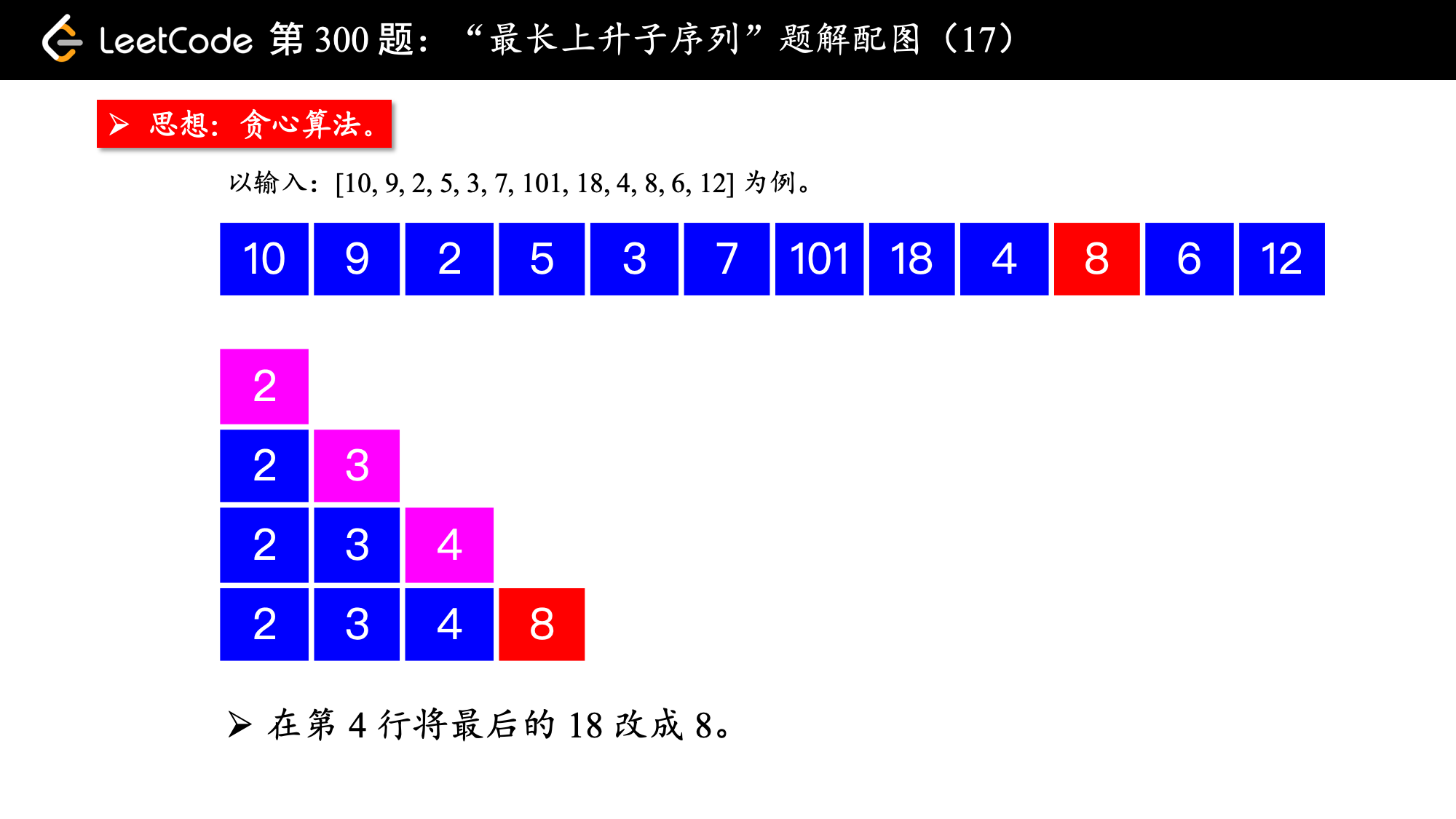 ,
, ,
, ,
, ,
,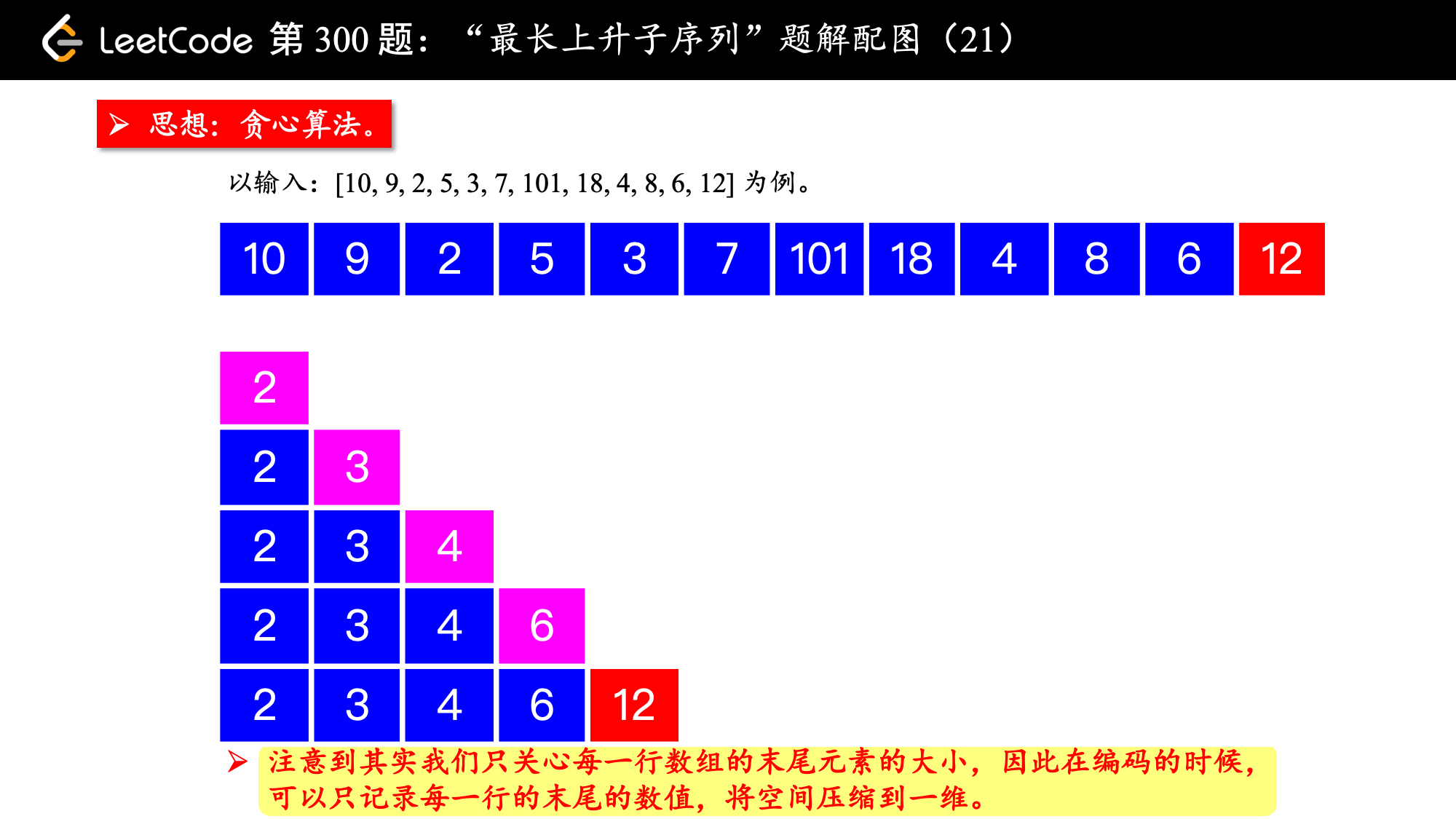
算法的执行流程:
1、设置一个有序数组 tail,初始时为空;
数组命名为
tail即 PPT 中各个行表示的数组(是一个“上升子序列”)的结尾,注意:有序数组tail虽然有“上升”的性质,但它不是每时每刻都表示问题中的“最长上升子序列”(下文还会强调),不能命名为LIS,有序数组tail是用于求解LIS问题的辅助数组。
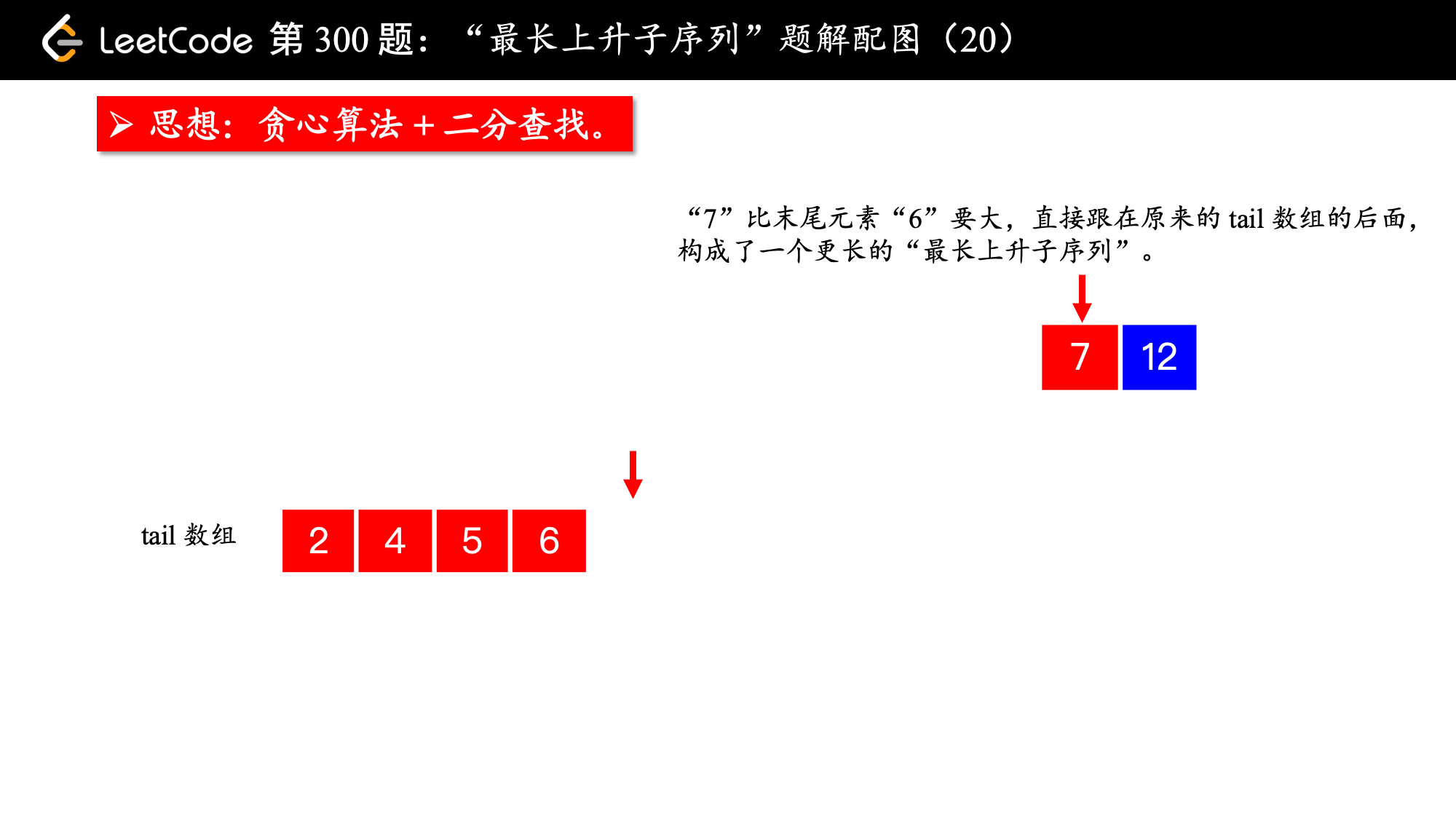
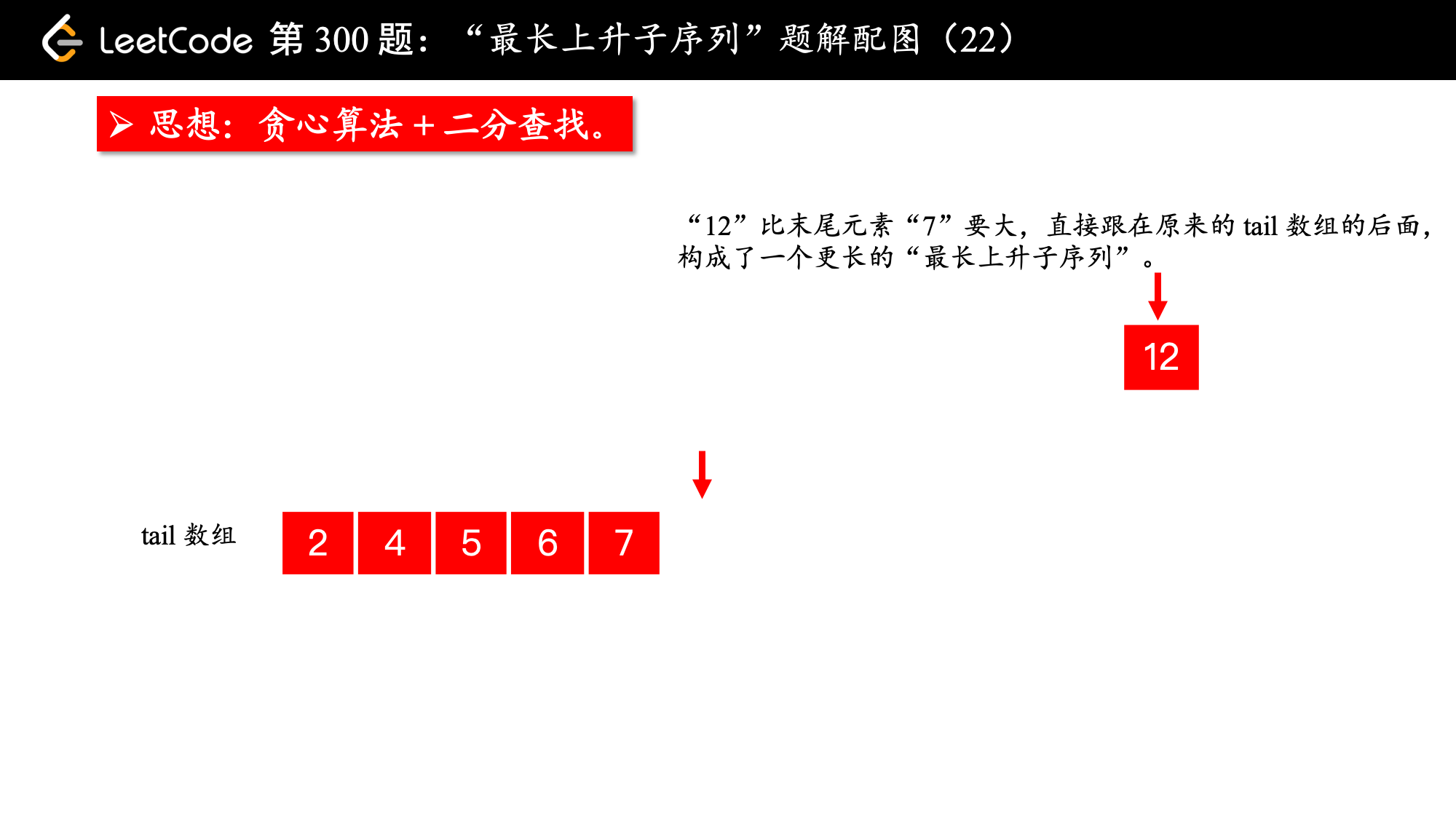
2、在遍历数组 nums 的过程中,每来一个新数 num,如果这个数严格大于有序数组 tail 的最后一个元素,就把 num 放在有序数组 tail 的后面,否则进入第 3 点;
注意:这里的大于是“严格”大于,不包括等于的情况。
3、在有序数组 tail 中查找第 1 个等于大于 num 的那个数,试图让它变小;
- 如果有序数组
tail中存在等于num的元素,什么都不做,因为以num结尾的最短的“上升子序列”已经存在; - 如果有序数组
tail中存在大于num的元素,找到第 1 个,让它变小,这样我们就找到了一个“结尾更小”的“相同长度”的上升子序列。
这一步可以使用“二分查找法”。
4、遍历新的数 num ,先尝试上述第 2 点,第 2 点行不通则执行第 3 点,直到遍历完整个数组 nums,最终有序数组 tail 的长度,就是所求的“最长上升子序列”的长度。
算法的关键之处:
以上算法能够奏效的关键是:
最开始提到的“基本思想”,可以认为是一种“贪心选择”的思想:只要让前面的数尽量小,在算法的执行过程中,第 2 点被执行的机会就越多。
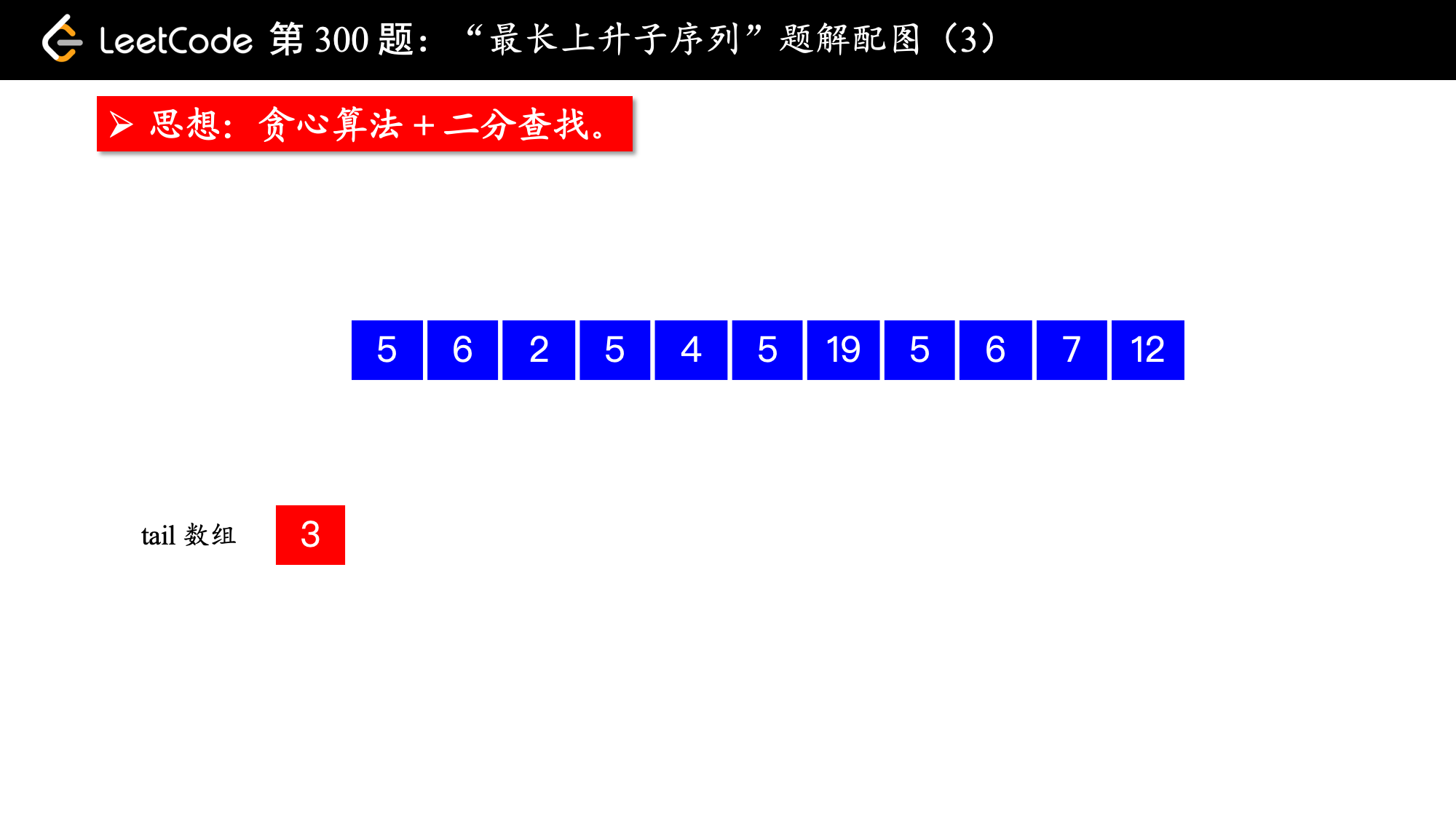
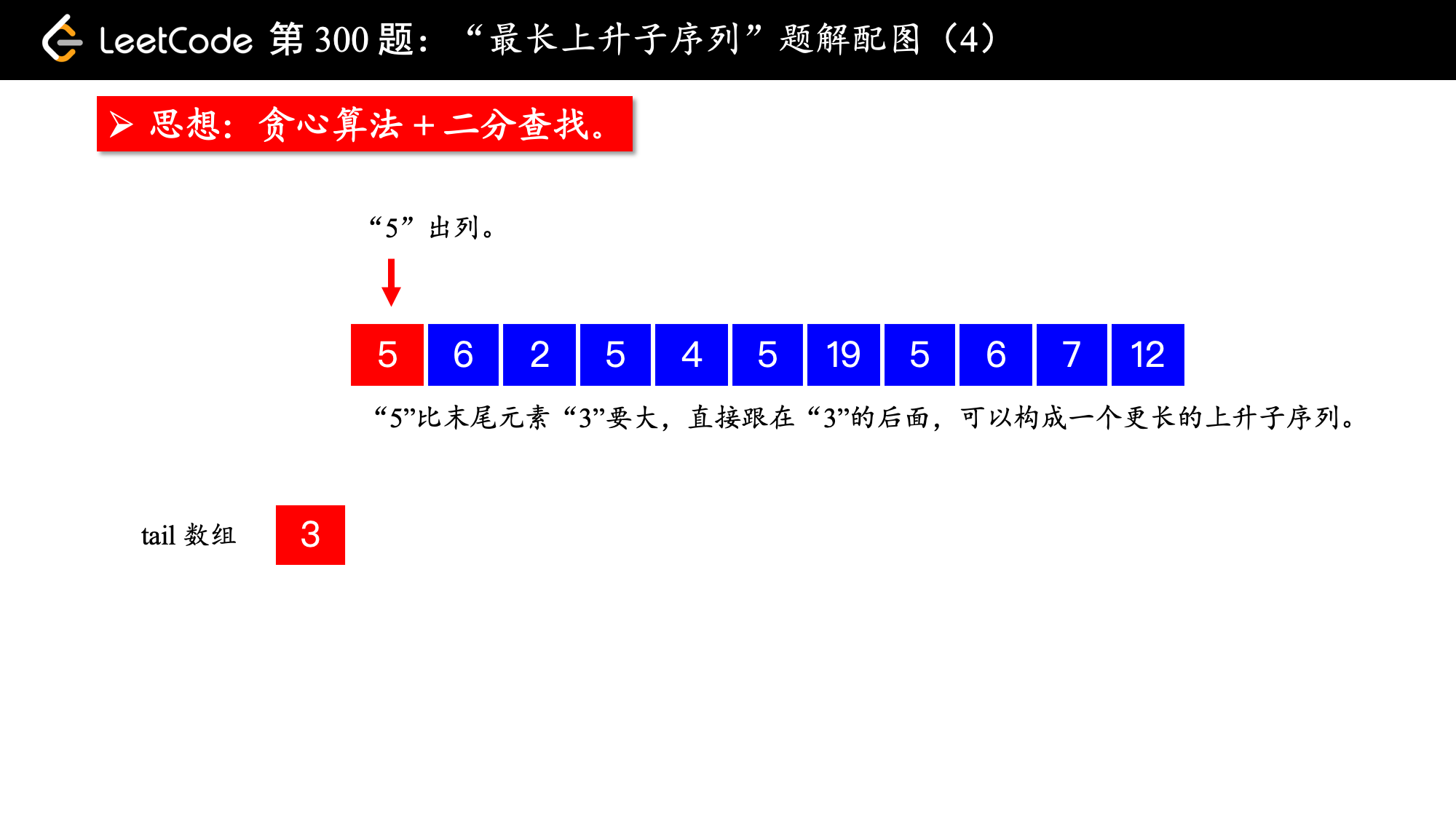
下面从算法运行的角度看一个具体的例子,此时我们使用的辅助数组是一维的,以便于您理解算法的基本思想和执行流程。
以下 2 点注意事项,请读者结合示例认真体会。
注意事项:
1、虽然有序数组
tail是升序数组,但是这个数组并不是每时每刻都表示题目要求的那个“最长上升子序列”,这一点你可以在我上面的例子中找到例证;
有序数组 tail 可以这样理解:
tail[i]表示长度为i + 1(因为i表示索引,i + 1表示长度)的所有“上升子序列”里结尾最小的元素。
因此, 有序数组 tail 的长度就是题目所求的“最长上升子序列”的长度。
2、“贪心选择性质”保证了算法流程的第 2 点有更多机会被执行。
下面看一个具体的例子,理解算法是如何借助一个一维数组完成“最长上升子序列”的长度的求解过程。
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
 ,
, ,
, ,
, ,
,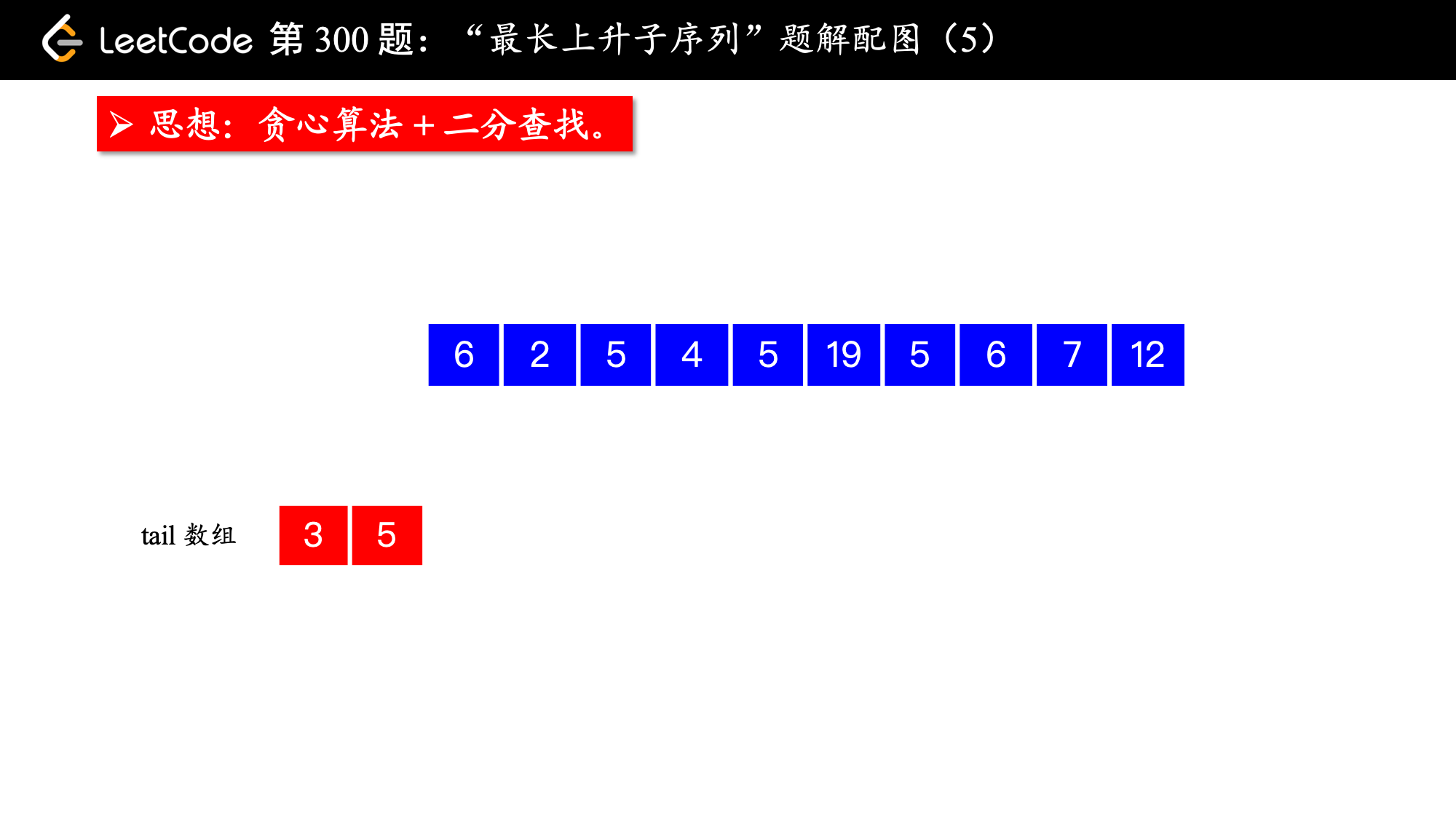 ,
,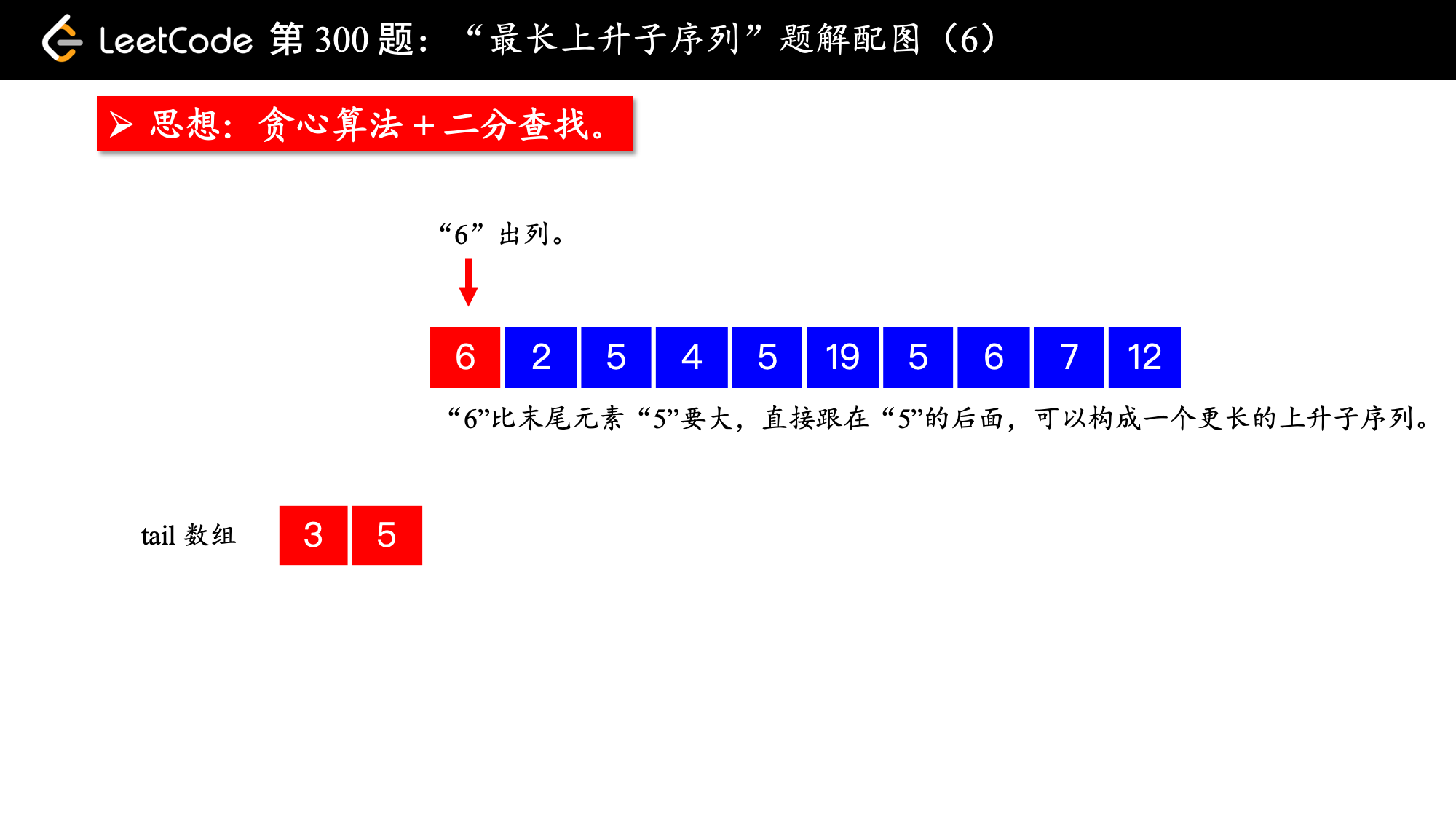 ,
,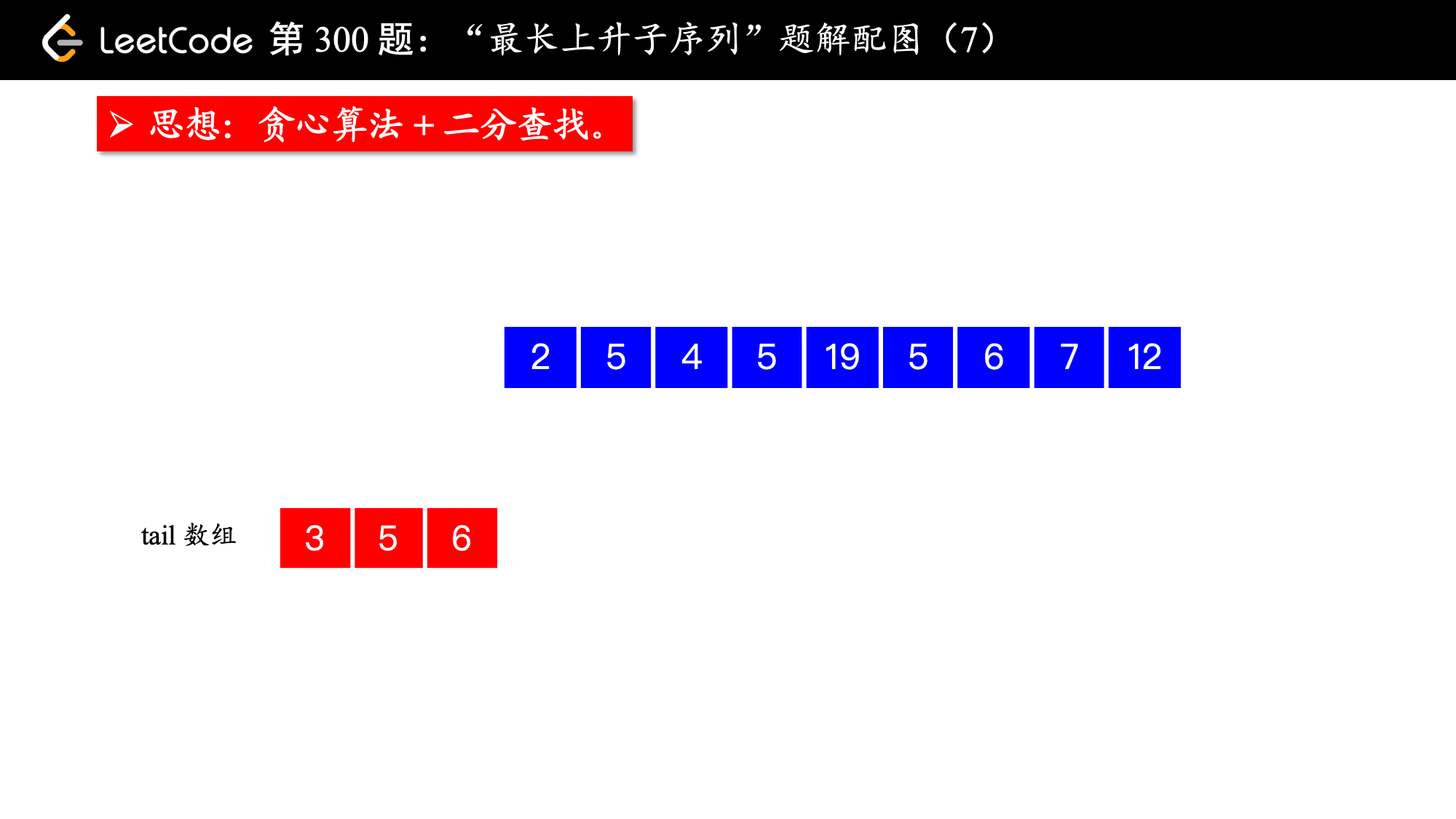 ,
,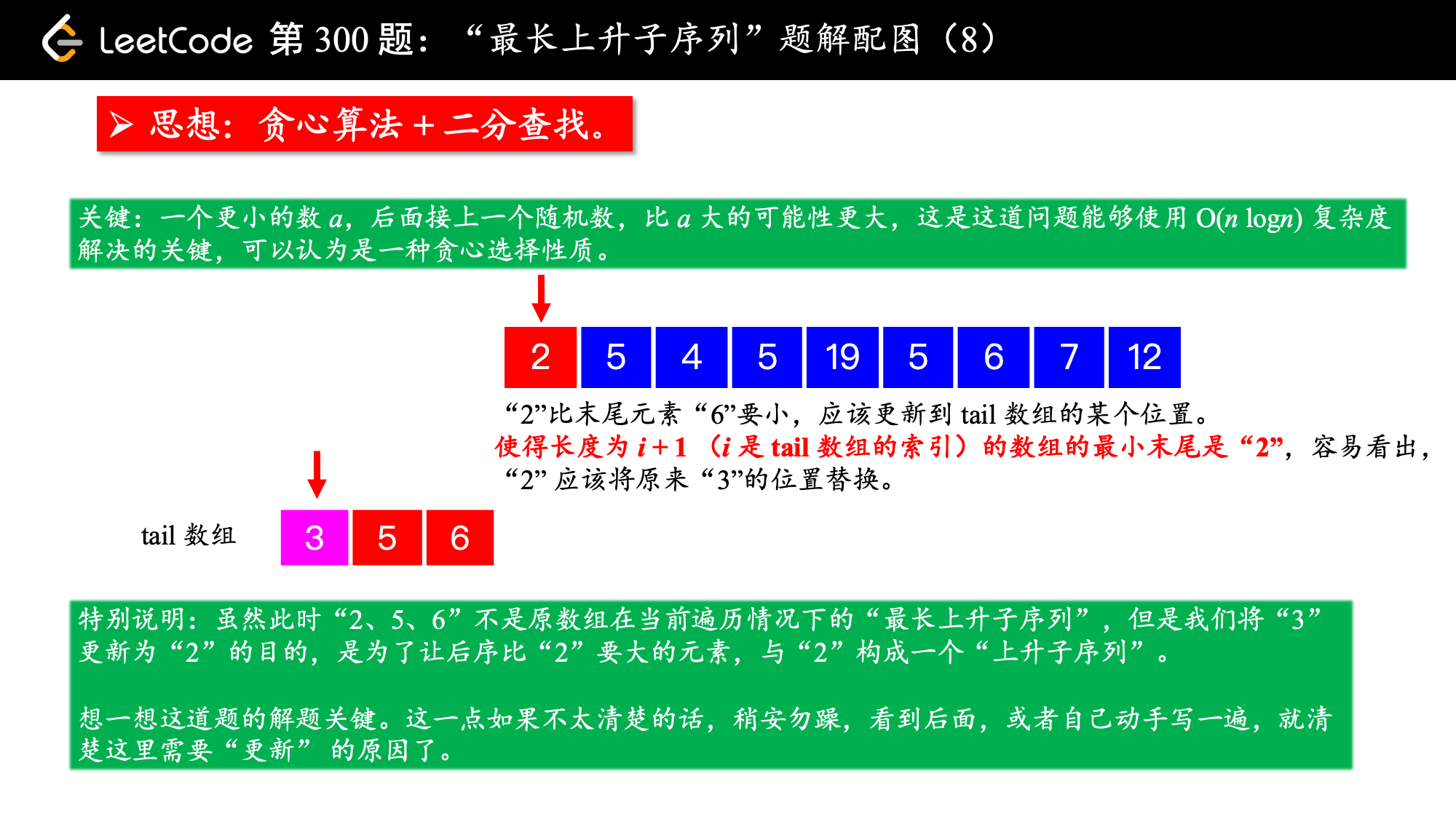 ,
,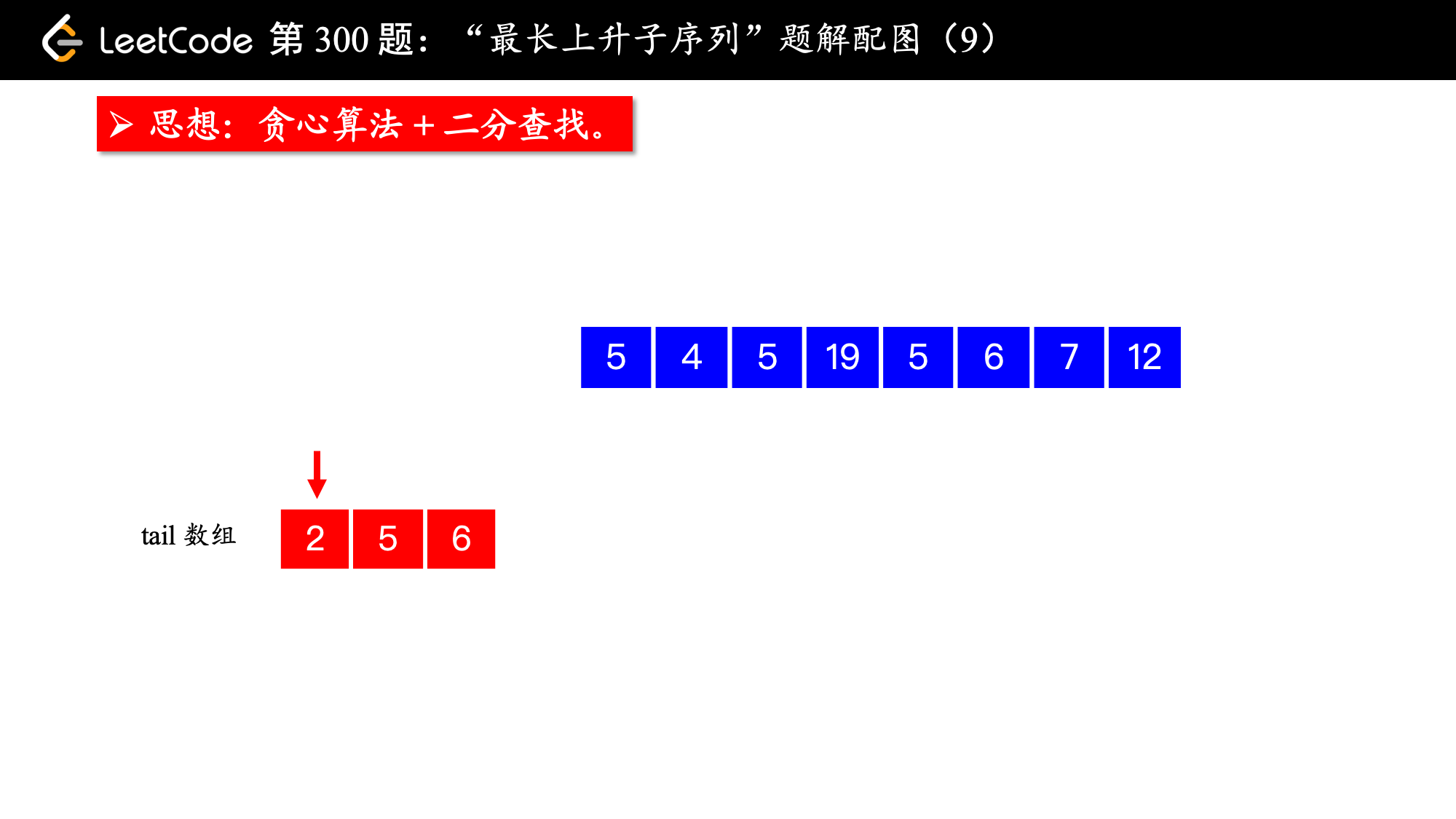 ,
,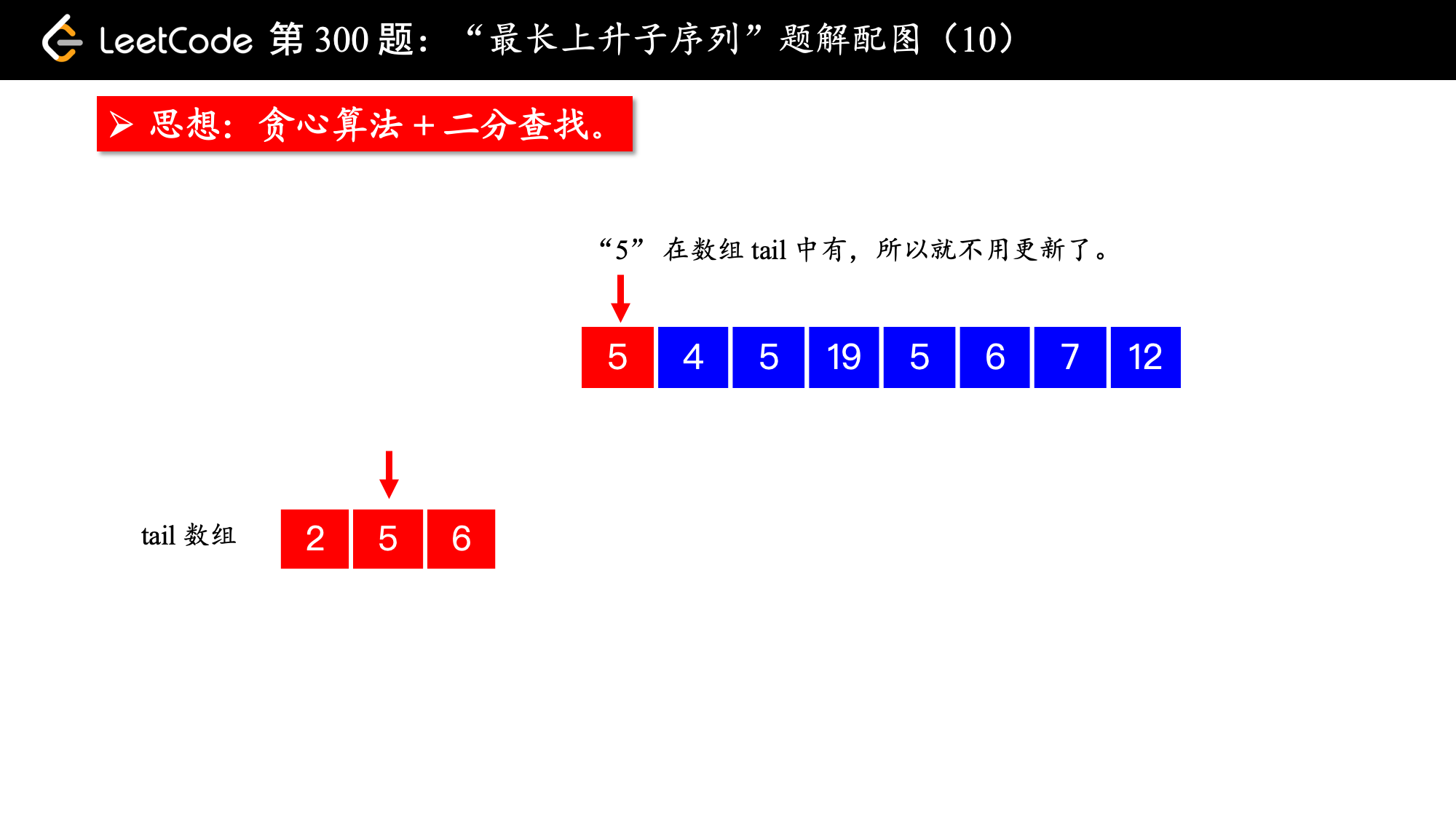 ,
,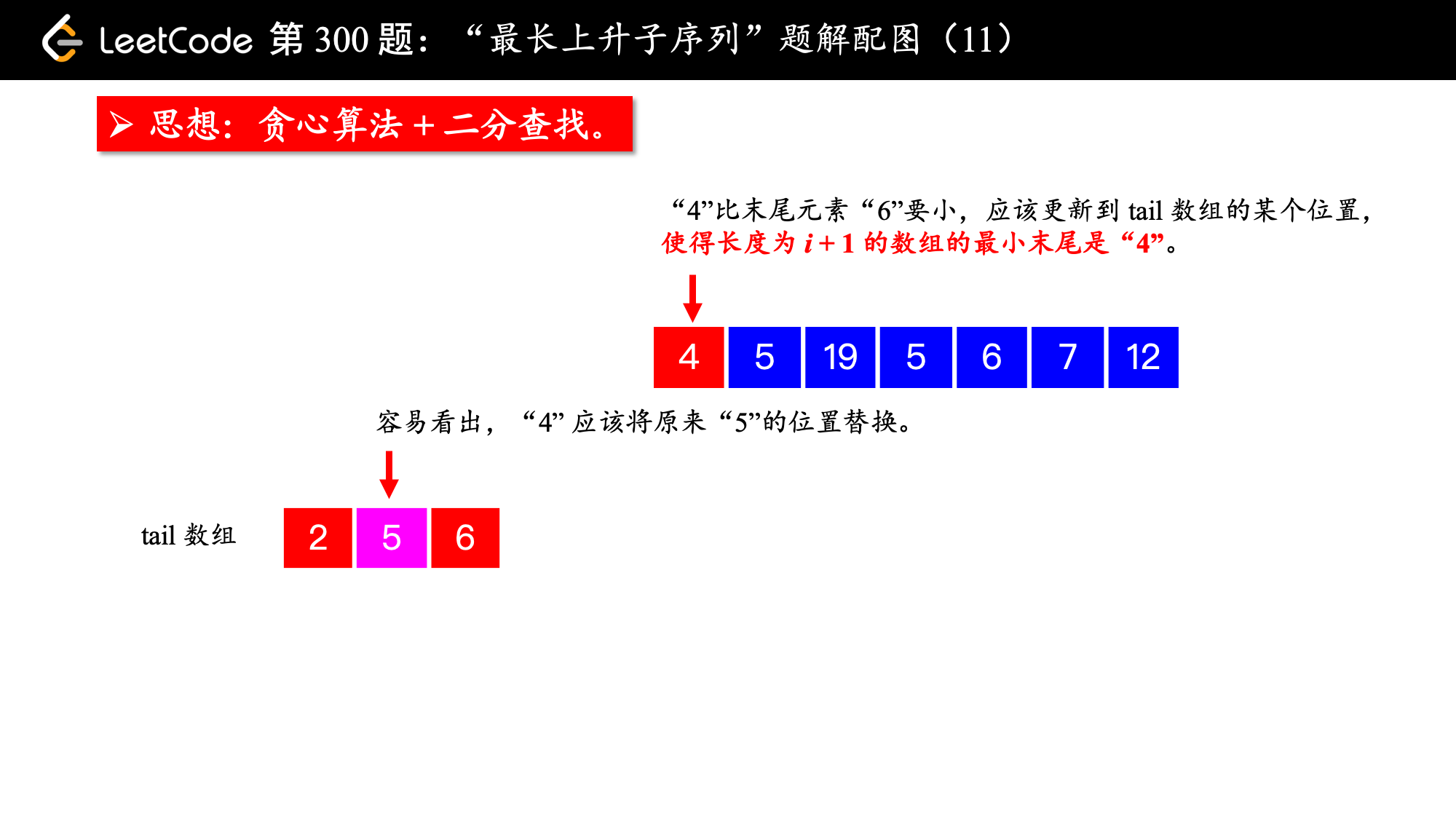 ,
, ,
,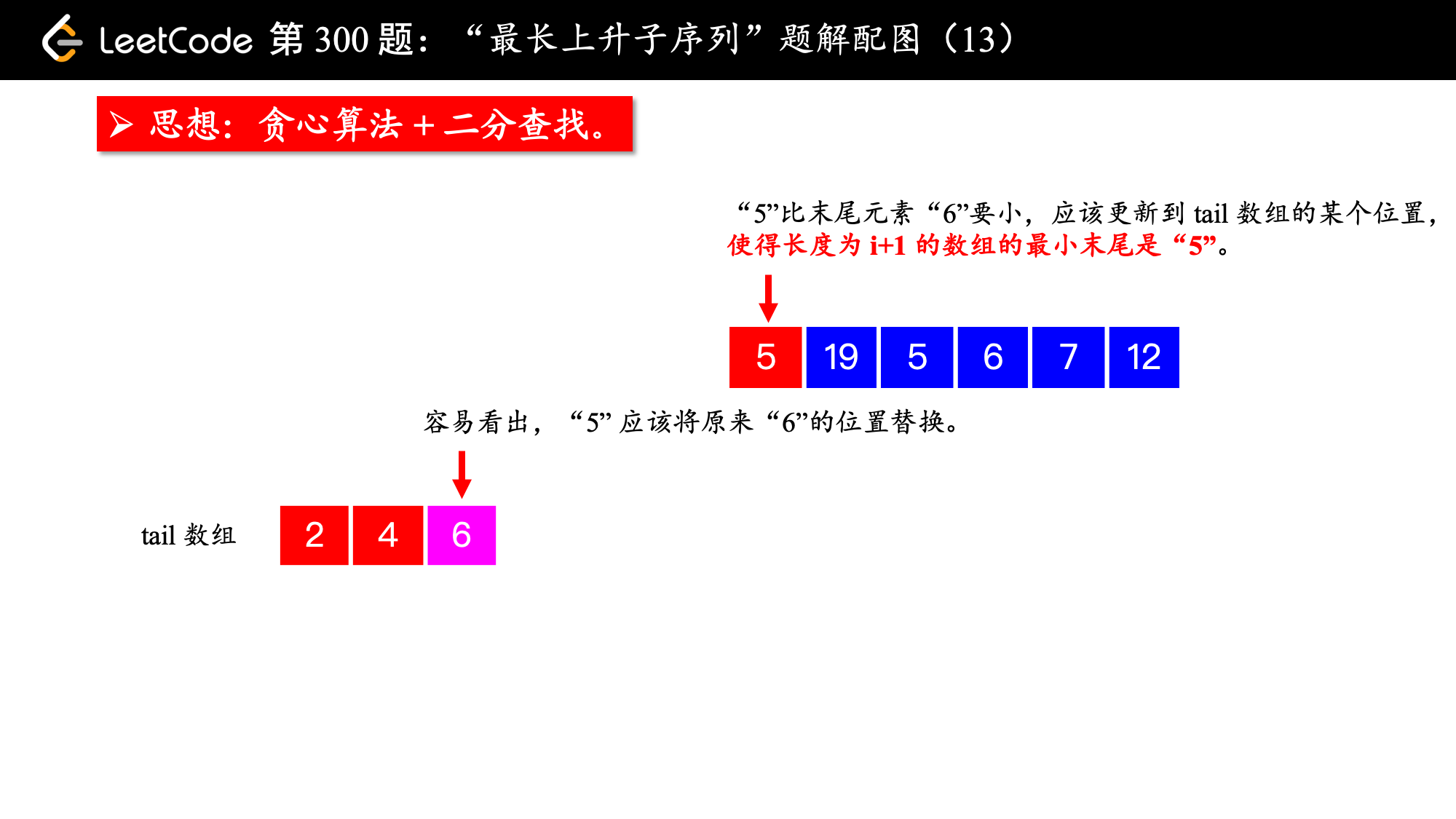 ,
, ,
,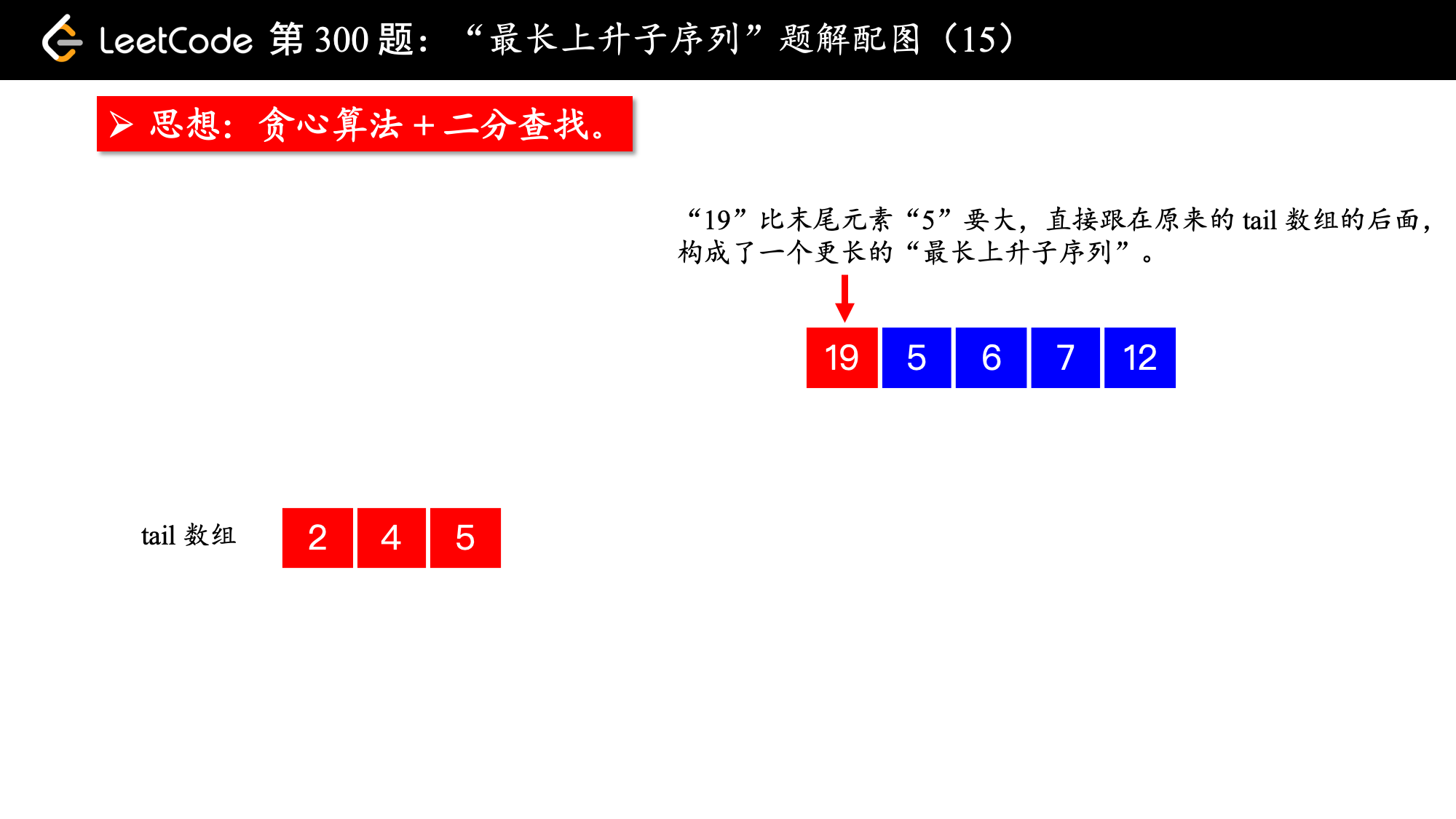 ,
,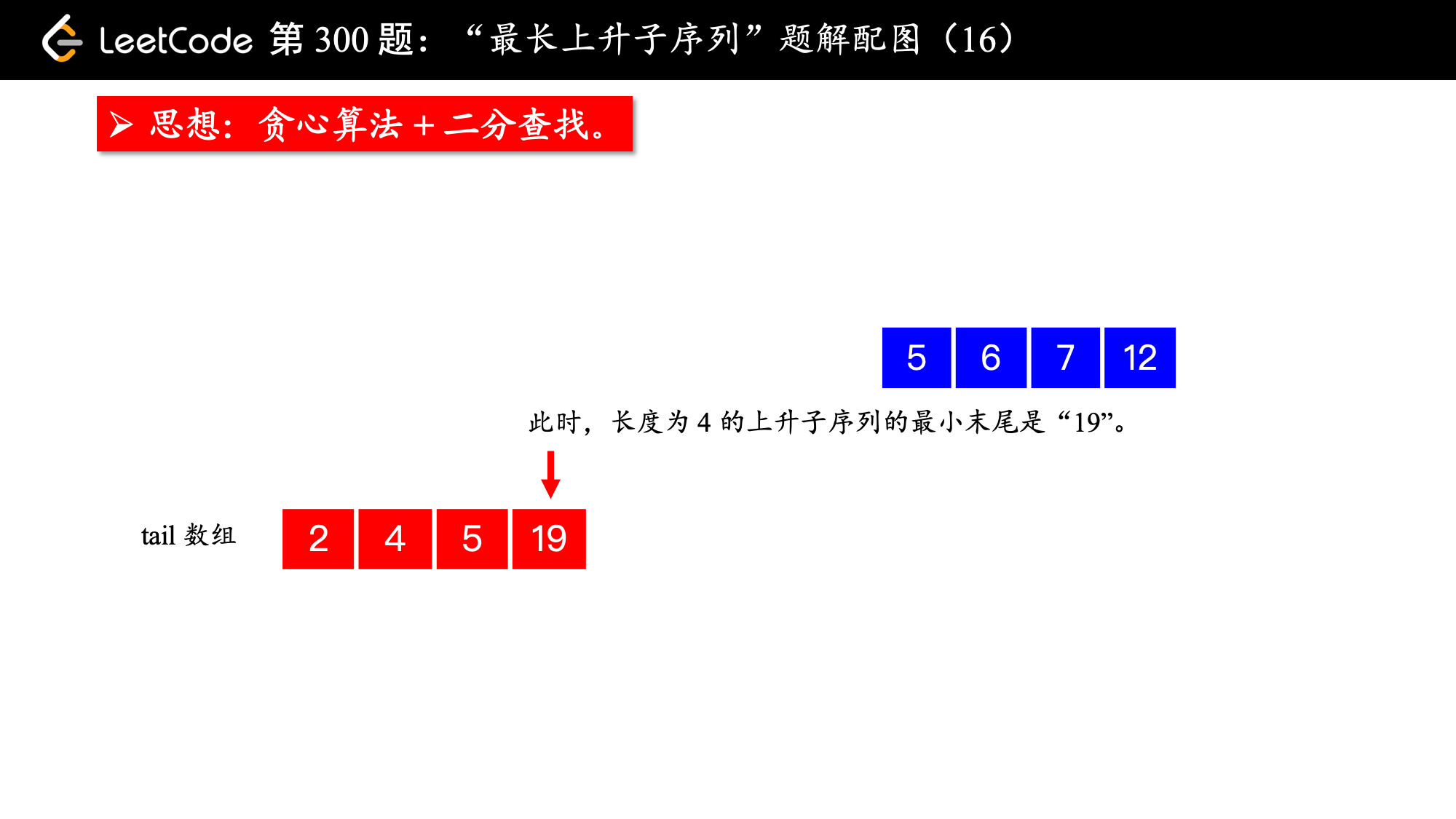 ,
,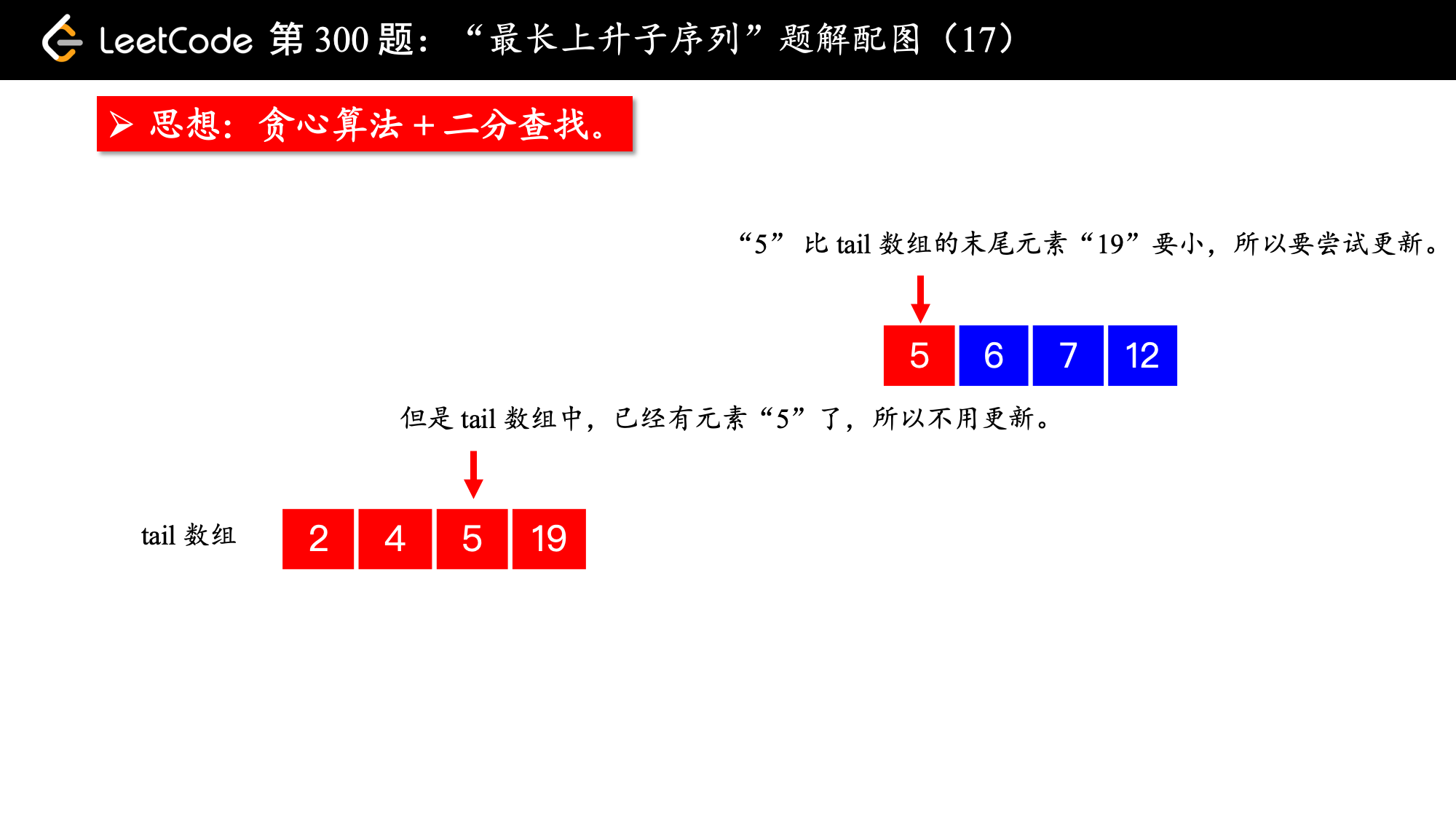 ,
,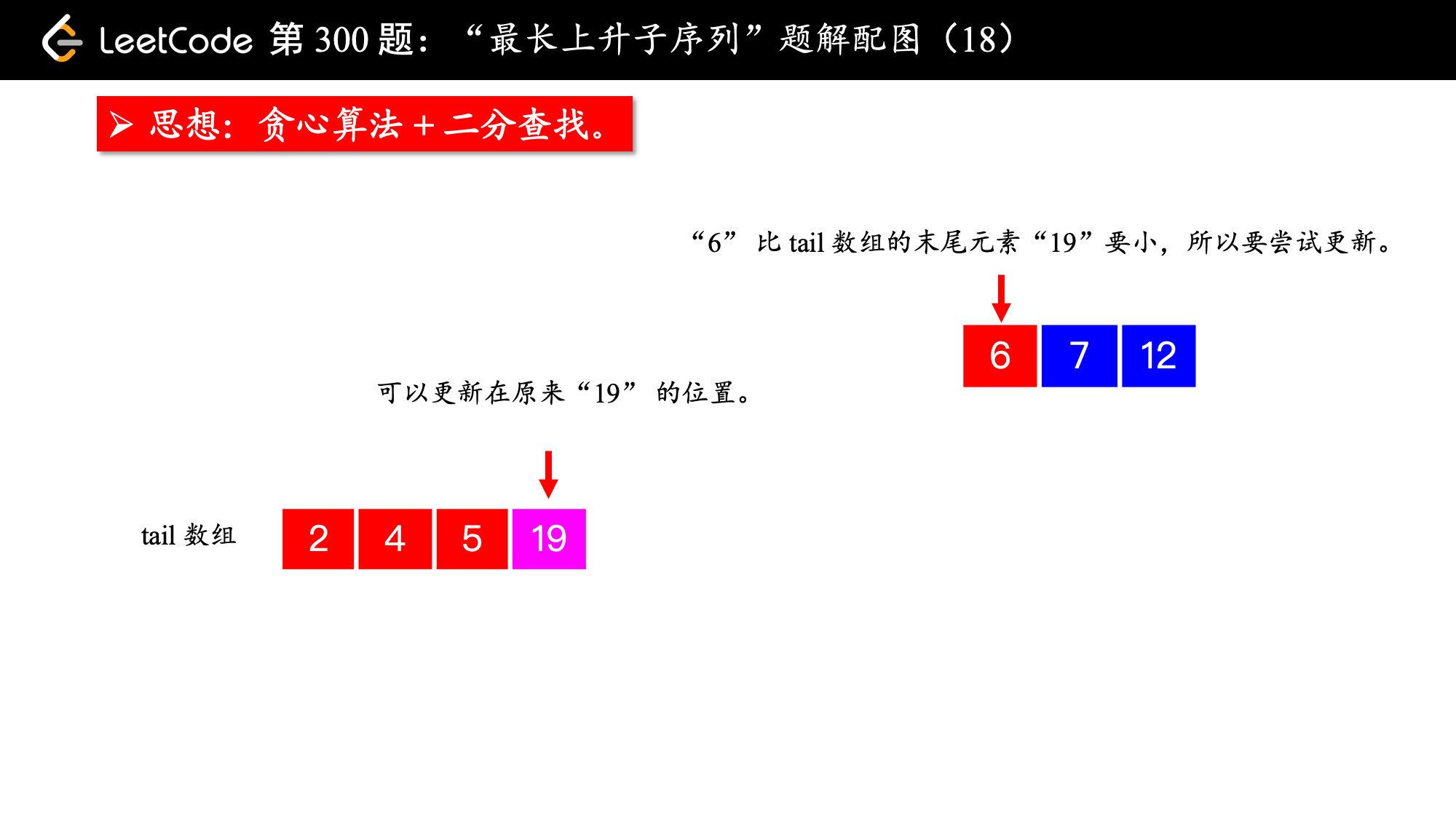 ,
, ,
, ,
, ,
, ,
,
下面是本解法的参考代码,在这个参考代码中,我使用了一个二分查找法的模板,我把使用这个二分查找法模板的优点、注意事项和调试方法都写在了「力扣 第 35 题:“搜索插入位置”的题解: 《特别好用的二分查找法模板(Python 代码、Java 代码)》,如果你能够分析出我给出的两个 Python 版本代码和两个 Java 版本代码关于二分查找的不同之处,那就说明你已经掌握了这个模板,相信会对您今后准确使用二分查找法有一定帮助。
理解了这个方法以后,朋友们不妨尝试挑战一下「力扣」第 354 题:“俄罗斯套娃信封问题”。
参考代码:
参考代码 2:严格按照以上算法执行流程写出来的代码。
Python 代码:
from typing import List
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
size = len(nums)
# 特判
if size < 2:
return size
# 为了防止后序逻辑发生数组索引越界,先把第 1 个数放进去
tail = [nums[0]]
for i in range(1, size):
# 【逻辑 1】比 tail 数组实际有效的末尾的那个元素还大
# 先尝试是否可以接在末尾
if nums[i] > tail[-1]:
tail.append(nums[i])
continue
# 使用二分查找法,在有序数组 tail 中
# 找到第 1 个大于等于 nums[i] 的元素,尝试让那个元素更小
left = 0
right = len(tail) - 1
while left < right:
# 选左中位数不是偶然,而是有原因的,原因请见 LeetCode 第 35 题题解
# mid = left + (right - left) // 2
mid = (left + right) >> 1
if tail[mid] < nums[i]:
# 中位数肯定不是要找的数,把它写在分支的前面
left = mid + 1
else:
right = mid
# 走到这里是因为【逻辑 1】的反面,因此一定能找到第 1 个大于等于 nums[i] 的元素,因此无需再单独判断
tail[left] = nums[i]
return len(tail)
Python 代码:
public class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
// 特判
if (len <= 1) {
return len;
}
// tail 数组的定义:长度为 i + 1 的上升子序列的末尾最小是几
int[] tail = new int[len];
// 遍历第 1 个数,直接放在有序数组 tail 的开头
tail[0] = nums[0];
// end 表示有序数组 tail 的最后一个已经赋值元素的索引
int end = 0;
for (int i = 1; i < len; i++) {
// 【逻辑 1】比 tail 数组实际有效的末尾的那个元素还大
if (nums[i] > tail[end]) {
// 直接添加在那个元素的后面,所以 end 先加 1
end++;
tail[end] = nums[i];
} else {
// 使用二分查找法,在有序数组 tail 中
// 找到第 1 个大于等于 nums[i] 的元素,尝试让那个元素更小
int left = 0;
int right = end;
while (left < right) {
// 选左中位数不是偶然,而是有原因的,原因请见 LeetCode 第 35 题题解
// int mid = left + (right - left) / 2;
int mid = left + ((right - left) >>> 1);
if (tail[mid] < nums[i]) {
// 中位数肯定不是要找的数,把它写在分支的前面
left = mid + 1;
} else {
right = mid;
}
}
// 走到这里是因为 【逻辑 1】 的反面,因此一定能找到第 1 个大于等于 nums[i] 的元素
// 因此,无需再单独判断
tail[left] = nums[i];
}
// 调试方法
// printArray(nums[i], tail);
}
// 此时 end 是有序数组 tail 最后一个元素的索引
// 题目要求返回的是长度,因此 +1 后返回
end++;
return end;
}
// 调试方法,以观察是否运行正确
private void printArray(int num, int[] tail) {
System.out.print("当前数字:" + num);
System.out.print("\t当前 tail 数组:");
int len = tail.length;
for (int i = 0; i < len; i++) {
if (tail[i] == 0) {
break;
}
System.out.print(tail[i] + ", ");
}
System.out.println();
}
public static void main(String[] args) {
int[] nums = new int[]{3, 5, 6, 2, 5, 4, 19, 5, 6, 7, 12};
Solution8 solution8 = new Solution8();
int lengthOfLIS = solution8.lengthOfLIS(nums);
System.out.println("最长上升子序列的长度:" + lengthOfLIS);
}
}
参考代码 3:与“参考代码 1 ”等价的代码,区别仅在于“二分查找法”候选区间的选择。
Python 代码:
from typing import List
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
size = len(nums)
# 特判
if size < 2:
return size
# tail 数组的定义:长度为 i + 1 的上升子序列的末尾最小是几
# 遍历第 1 个数,直接放在有序数组 tail 的开头
tail = [nums[0]]
for i in range(1, size):
# 找到大于等于 num 的第 1 个数,试图让它变小
left = 0
# 因为有可能 num 比 tail 数组中的最后一个元素还要大,
# 【逻辑 1】所以右边界应该设置为 tail 数组的长度
right = len(tail)
while left < right:
# 选左中位数不是偶然,而是有原因的,原因请见 LeetCode 第 35 题题解
# mid = left + (right - left) // 2
mid = (left + right) >> 1
if tail[mid] < nums[i]:
# 中位数肯定不是要找的数,把它写在分支的前面
left = mid + 1
else:
right = mid
if left == len(tail):
tail.append(nums[i])
else:
# 因为【逻辑 1】,因此一定能找到第 1 个大于等于 nums[i] 的元素,因此无需再单独判断,直接更新即可
tail[left] = nums[i]
return len(tail)
Python 代码:
public class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
// 特判
if (len <= 1) {
return len;
}
// tail 数组的定义:长度为 i + 1 的上升子序列的末尾最小是几
int[] tail = new int[len];
// 遍历第 1 个数,直接放在有序数组 tail 的开头
tail[0] = nums[0];
// end 表示有序数组 tail 的最后一个已经赋值元素的索引
int end = 0;
for (int i = 1; i < len; i++) {
int left = 0;
// 这里,因为当前遍历的数,有可能比有序数组 tail 数组实际有效的末尾的那个元素还大
// 【逻辑 1】因此 end + 1 应该落在候选区间里
int right = end + 1;
while (left < right) {
// 选左中位数不是偶然,而是有原因的,原因请见 LeetCode 第 35 题题解
// int mid = left + (right - left) / 2;
int mid = (left + right) >>> 1;
if (tail[mid] < nums[i]) {
// 中位数肯定不是要找的数,把它写在分支的前面
left = mid + 1;
} else {
right = mid;
}
}
// 因为 【逻辑 1】,因此一定能找到第 1 个大于等于 nums[i] 的元素
// 因此,无需再单独判断,直接更新即可
tail[left] = nums[i];
// 但是 end 的值,需要更新,当前仅当更新位置在当前 end 的下一位
if (left == end + 1) {
end++;
}
}
// 调试方法
// printArray(nums[i], tail);
// 此时 end 是有序数组 tail 最后一个元素的索引
// 题目要求返回的是长度,因此 +1 后返回
end++;
return end;
}
// 调试方法,以观察是否运行正确
private void printArray(int num, int[] tail) {
System.out.print("当前数字:" + num);
System.out.print("\t当前 tail 数组:");
int len = tail.length;
for (int i = 0; i < len; i++) {
if (tail[i] == 0) {
break;
}
System.out.print(tail[i] + ", ");
}
System.out.println();
}
public static void main(String[] args) {
int[] nums = new int[]{3, 5, 6, 2, 5, 4, 19, 5, 6, 7, 12};
Solution9 solution9 = new Solution9();
int lengthOfLIS = solution9.lengthOfLIS(nums);
System.out.println("最长上升子序列的长度:" + lengthOfLIS);
}
}
复杂度分析:
- 时间复杂度:,遍历数组使用了 ,二分查找法使用了 。
- 空间复杂度:,开辟有序数组
tail的空间至多和原始数组一样。