LeetCode 第 3 题:“无重复字符的最长子串”题解
题解地址:滑动窗口、哈希表优化 + 动态规划、滚动变量(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:3. 无重复字符的最长子串。
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2:
输入: "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。 示例 3:
输入: "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
滑动窗口、哈希表优化 + 动态规划、滚动变量(Python 代码、Java 代码)
思路分析:
容易分析出,重复的地方出现在连续子串的一头一尾,显然这个问题是一个滑动窗口问题,因此这道题就转化为“滑动窗口”的最大值(具体说是最大值 - 1,因为重复的只能算 1 个)问题,可以使用“滑动窗口”的一些技巧来完成。
另外,最优化问题“感觉”可以使用“动态规划”完成,于是就得到了这道题的两个思路。
方法一:滑动窗口
“滑动窗口”的套路也很直接,这种办法也叫“双指针”。
算法步骤:
1、“窗口”的右边界一直向右边滑动,直到发现“窗口”内的元素出现了重复,或者右边界超过了字符串的末尾,在右边界扩张的过程中,“滑动窗口”的长度在逐渐增大,此时记录下最大值;
2、只要出现了“重复”,“窗口”的右边界停止,此时左边界向右边移动,直到“滑动窗口”内没有重复的元素,跳转到第 1 步。
说明:请留意第 2 点,被着重强调的部分,接下来我们会针对这一点进行优化。
因为要判断“窗口”内的元素出现了重复,可以使用数组记录字符频率,或者使用哈希表。思路并不难,但是在编码上有一些注意事项,我写在了下面的注释中。
参考代码 1:
Python 代码:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
size = len(s)
# 特判
if size < 2:
return size
left = 0
# 滑动窗口的逻辑是尝试向右移动一位,因此,初始值是 -1
right = -1
# 设置成 128 与测试用例有关
counter = [0 for _ in range(128)]
# 因为自己一定是不重复的子串,在字符串非空的情况下,至少结果为 1
res = 1
# 认为左边界更重要,有重复的子串,我们记录左边,舍弃右边,因此左边界如果越界了,算法停止
while left < size:
# right + 1 表示最多到 len - 1
# counter[s.charAt(right + 1)] == 0 表示在 [left, right] 这个区间里没有出现
if right + 1 < size and counter[ord(s[right + 1])] == 0:
# 表示没有重复元素,right 可以加 1
counter[ord(s[right + 1])] += 1
right += 1
else:
# 如果下一个字符已经越界了,或者右边第 1 个字母是频率数组是曾经出现过的
# 把左边从频数数组中挪掉,频数减 1
counter[ord(s[left])] -= 1
left += 1
# 经过上面的分支,窗口 [left, right] 内一定没有重复元素,故记录最大值
res = max(res, right - left + 1)
return res
Java 代码:
public class Solution {
public int lengthOfLongestSubstring(String s) {
int len = s.length();
// 特判
if (len < 2) {
return len;
}
int[] counter = new int[128];
int res = 1;
int left = 0;
// 滑动窗口的逻辑是尝试向右移动一位,因此,初始值是 -1
int right = -1;
// 认为左边界更重要,有重复的子串,我们记录左边,舍弃右边,因此左边界如果越界了,算法停止
while (left < len) {
// right + 1 表示最多到 len - 1
// counter[s.charAt(right + 1)] == 0 表示在 [left, right] 这个区间里没有出现
if (right + 1 < len && counter[s.charAt(right + 1)] == 0) {
// 右边第 1 个字母加入频率数组,频数 + 1
counter[s.charAt(right + 1)]++;
right++;
} else {
// 如果下一个字符已经越界了,或者右边第 1 个字母是频率数组是曾经出现过的
// 把左边从频数数组中挪掉,频数减 1
counter[s.charAt(left)]--;
left++;
}
// 经过上面的分支,窗口 [left, right] 内一定没有重复元素,故记录最大值
res = Math.max(res, right - left + 1);
}
return res;
}
}
复杂度分析:
- 时间复杂度:,这里 是数组的长度。
- 空间复杂度:,因为使用到的临时变量和
counter数组的长度都是常数个,不因问题的规模而改变,故空间复杂度是 。
“滑动窗口”方法的优化:
注意到上面“算法步骤”的第 2 点:
只要出现了“重复”,“窗口”的右边界停止,此时左边界向右边移动,直到“滑动窗口”内没有重复的元素,跳转到第 1 步。
这里“滑动窗口”内没有元素的时候,一定是左边界“前进”到和右边界相等的元素的时候,因此,在右边界“滑动”的过程中,已经出现过的字符的索引就很重要,使用哈希表记录索引的方式,可以让左边界直接跳到它后面的第 1 个位置,因为下一个不重复的子串的左边至少出现在它后面的第 1 个位置。
“滑动窗口”内每个字符的频率其实至多是 2,刚刚要出现 2 的时候,我们就得马上让它减少到 1,体会这个边界条件。“减少到 1”这件事情,在记录索引位置的时候,不一定同时也要记录词频,只要这个索引不在“滑动窗口”之内,即在 left 之前,就可以认为不存在重复,综上所述,我们选择哈希表,以空间换时间。
思路比较简单,还是编码的时候有细节要处理。
参考代码 2:
Python 代码:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
# 特判
size = len(s)
if size < 2:
return size
# key 为字符,val 记录了当前读到的字符的索引,在每轮循环的最后更新
d = dict()
left = 0
# 非空的时候,结果至少是 1 ,因此初值可以设置成为 1
res = 1
for right in range(size):
# d[s[right]] >= left,表示重复出现在滑动窗口内
# d[s[right]] < left 表示重复出现在滑动窗口之外,之前肯定计算过了
if s[right] in d and d[s[right]] >= left:
# 下一个不重复的子串至少在之前重复的那个位置之后
# 【特别注意】快在这个地方,左边界直接跳到之前重复的那个位置之后
left = d[s[right]] + 1
# 此时滑动窗口内一定没有重复元素
res = max(res, right - left + 1)
# 无论如何都更新位置
d[s[right]] = right
return res
Java 代码:
import java.util.HashMap;
import java.util.Map;
public class Solution {
public int lengthOfLongestSubstring(String s) {
int len = s.length();
// 特判
if (len < 2) {
return len;
}
int left = 0;
// 非空的时候,结果至少是 1 ,因此初值可以设置成为 1
int res = 1;
// key 为字符,val 记录了当前读到的字符的索引,在每轮循环的最后更新
Map<Character, Integer> map = new HashMap<>();
for (int right = 0; right < len; right++) {
// 右边界没有重复的时候,直接向右边扩张就好了
// 右边界有重复的时候,只要在滑动窗口内,我们就得更新
// 如果在滑动窗口之外,一定是之前被计算过的
if (map.containsKey(s.charAt(right))) {
if (map.get(s.charAt(right)) >= left) {
// 下一个不重复的子串至少在之前重复的那个位置之后
// 【特别注意】快在这个地方,左边界直接跳到之前重复的那个位置之后
left = map.get(s.charAt(right)) + 1;
}
}
// 此时滑动窗口内一定没有重复元素
res = Math.max(res, right - left + 1);
// 无论如何都更新位置
map.put(s.charAt(right), right);
}
return res;
}
}
复杂度分析:
- 时间复杂度:,这里 是数组的长度。
- 空间复杂度:,这里使用哈希表,用空间换时间。
其实还可以再优化一点,因为左边界在“滑动”的过程中,只可能向左边走,因此,左边界取最大值即可。
参考代码 3:
Python 代码:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
size = len(s)
# 特判
if size < 2:
return size
res = 0
left = 0
d = dict()
for right in range(size):
if s[right] in d:
# 更新 left 的位置,left 的位置只能越来越后
left = max(left, d[s[right]] + 1)
# 从 [left, right] 这个区间里,都没有重复的字符串
# [3, 4, 5, 6] 这个区间一共有 6 - 3 + 1 = 4 个元素
# 每一次都要更新 map 和 res
res = max(res, right - left + 1)
# 不论怎么样都要更新 map
d[s[right]] = right
return res
Java 代码:
import java.util.HashMap;
import java.util.Map;
public class Solution {
public int lengthOfLongestSubstring(String s) {
int len = s.length();
// 特判
if (len < 2) {
return len;
}
int res = 1;
Map<Character, Integer> map = new HashMap<>();
int left = 0;
for (int right = 0; right < len; right++) {
Character c = s.charAt(right);
if (map.containsKey(c)) {
left = Math.max(left, map.get(c) + 1);
}
res = Math.max(res, right - left + 1);
map.put(c, right);
}
return res;
}
}
复杂度分析同上。
方法二:动态规划
子串问题,如果就使用原问题定义的状态,子串在任何位置都可能出现,在推导状态转移方程的时候,会遇到很多不确定的因素,参考「力扣」第 53 题:“最大子序和”、「力扣」第 300 题:“最长上升子序列”的状态定义,我们认为子串一定要以某一个字符结尾,那么就让 dp[i] 定义成以 s[i] 结尾的“最长不重复子串”的长度,可以帮助我们推导“状态转移方程”。
1、“状态”的定义
dp[i]:以 s[i] 结尾的最长不重复子串的长度。
如果“状态”的定义不是问题的定义,就不能把最后一个状态返回回去。因此还要思考一下,输出是什么。
输出:dp[0]、dp[1]、……、dp[n - 1] 中的最大者,这里 n 是字符串的长度。
2、推导“状态转移方程”
这里我们尝试推导 dp[i] 与 dp[i - 1] 的关系,那当然要看 s[i] 啦,如果 s[i] 在滑动窗口内没有出现过,那么 s[i] 就可以出现在 dp[i - 1] 表示的那个“最长不重复子串”的后面,表示一个更长的“最长不重复子串”,此时 dp[i] = dp[i - 1] + 1。
“ s[i] 之前有没有出现过”这件事情,我们恐怕还得借助“哈希表”或者数组。
下面就要考虑 s[i] 在滑动窗口内出现过,一个比较容易想到的情况是,如果 dp[i] 特别短,它表示的“最长不重复子串”都够不着 s[i] 之前出现到的那个位置。
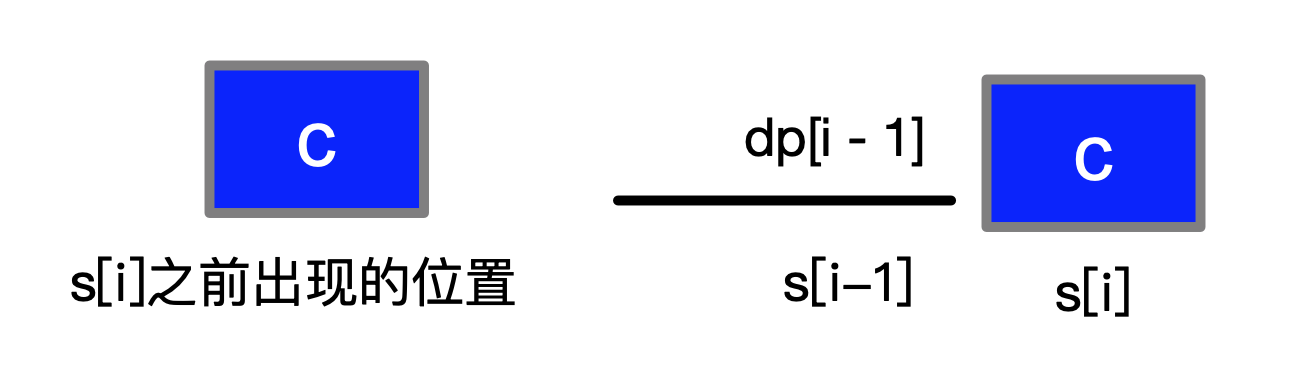
情况就和上面一样:s[i] 也可以出现在 dp[i - 1] 表示的那个“最长不重复子串”的后面,表示一个更长的“最长不重复子串”,此时 dp[i] = dp[i - 1] + 1。
下面我们就开始找边界条件,那就是 dp[i - 1] 表示的那个“最长不重复子串”的左边界刚刚好够到“s[i] 之前出现过的位置”,即 dp[i - 1] >= i - s[i] 之前出现过的位置,此时 dp[i] 就只能是当前位置和“s[i] 之前出现过的位置”这两个位置确定的那个“不重复子串”的长度,在纸上画一个具体的例子。
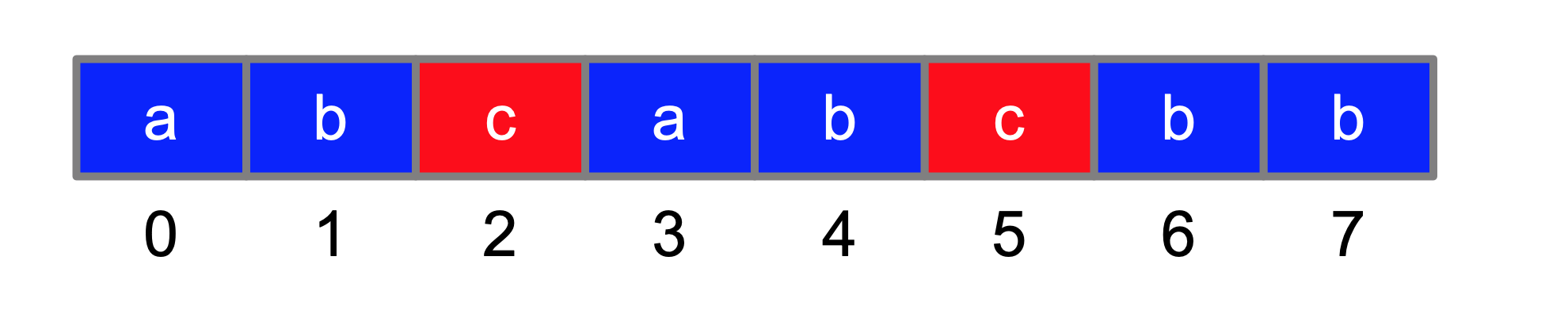
如果当前 i = 5,dp[i] 就是 i 减去“s[i] 之前出现过的位置”,即 ,记“最长不重复子串”的时候,你用索引 2 的 C 还是索引 5 的 C 都是可以的。
参考代码 4:
Python 代码:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
size = len(s)
# 特判
if size < 2:
return size
# dp[i] 表示以 s[i] 结尾的最长不重复子串的长度
# 因为自己肯定是不重复子串,所以初始值设置为 1
dp = [1 for _ in range(size)]
d = dict()
d[s[0]] = 0
# 因为要考虑 dp[i - 1],索引得从 1 开始,故 d[s[0]] = 0 得先写上
for i in range(1, size):
if s[i] in d:
if dp[i - 1] >= i - d[s[i]]:
dp[i] = i - d[s[i]]
else:
dp[i] = dp[i - 1] + 1
else:
dp[i] = dp[i - 1] + 1
# 设置字符与索引键值对
d[s[i]] = i
# 最后拉通看一遍最大值
return max(dp)
Java 代码:
import java.util.HashMap;
import java.util.Map;
public class Solution {
public int lengthOfLongestSubstring(String s) {
int len = s.length();
// 特判
if (len < 2) {
return len;
}
// dp[i] 表示以 s[i] 结尾的最长不重复子串的长度
// 因为自己肯定是不重复子串,所以初始值设置为 1
int[] dp = new int[len];
for (int i = 0; i < len; i++) {
dp[i] = 1;
}
Map<Character, Integer> map = new HashMap<>();
map.put(s.charAt(0), 0);
// 因为要考虑 dp[i - 1],索引得从 1 开始,故 d[s[0]] = 0 得先写上
for (int i = 1; i < len; i++) {
Character c = s.charAt(i);
if (map.containsKey(c)) {
if (dp[i - 1] >= i - map.get(c)) {
dp[i] = i - map.get(c);
} else {
dp[i] = dp[i - 1] + 1;
}
} else {
dp[i] = dp[i - 1] + 1;
}
// 设置字符与索引键值对
map.put(c, i);
}
// 最后拉通看一遍最大值
int res = dp[0];
for (int i = 1; i < len; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
}
复杂度分析:
- 时间复杂度:,这里 是数组的长度。
- 空间复杂度:。
注意到,这里有两个分支的结果是一样的,并且 d[i] 的值只与 dp[i - 1] 有关,我们可以把两个分支合并,并且把状态数组压缩成“滚动变量”。
参考代码:
Python 代码:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
# 特判
size = len(s)
if size < 2:
return size
pre = 1
res = 1
d = dict()
d[s[0]] = 0
# 因为要考虑 pre,索引得从 1 开始,故 d[s[0]] = 0 得先写上
for i in range(1, size):
if s[i] in d and pre >= i - d[s[i]]:
cur = i - d[s[i]]
else:
cur = pre + 1
# 设置字符与索引键值对
d[s[i]] = i
res = max(res, cur)
pre = cur
# 最后拉通看一遍最大值
return res
Java 代码:
public class Solution {
public int lengthOfLongestSubstring(String s) {
int len = s.length();
// 特判
if (len < 2) {
return len;
}
int pre = 1;
int res = 1;
Map<Character, Integer> map = new HashMap<>();
map.put(s.charAt(0), 0);
// 因为要考虑 pre,索引得从 1 开始,故 map.put(s.charAt(0), 0); 得先写上
for (int i = 1; i < len; i++) {
Character c = s.charAt(i);
int cur;
if (map.containsKey(c) && pre >= i - map.get(c)) {
cur = i - map.get(c);
} else {
cur = pre + 1;
}
// 设置字符与索引键值对
map.put(c, i);
pre = cur;
res = Math.max(res, cur);
}
return res;
}
}
- 时间复杂度:,这里 是数组的长度。
- 空间复杂度:,虽然“状态数组”被压缩成“滚动变量”,但“哈希表”仍占据了 个空间大小。