2. 二分查找的问题变种

事实上，「力扣」上的「二分查找」问题没有那么简单。例如，让我们找：

• 大于等于 target 的下标最小的元素；
• 小于等于 target 的下标最大的元素。

这样的问题有一个特点：当看到了 nums[mid] 恰好等于 target 的时候，还得继续查找，继续看看左边的元素的值，或者继续看看右边元素的值。如果不小心，很可能逻辑写错。如果还用「1. 二分查找的基本问题」介绍的方式编写代码，就没有那么容易：

• while 里面的 if 、else 该怎么写，有没有什么固定的思路？
• 退出循环以后，right 在左，left 在右，返回 left 还是 right 需要分类讨论。

本题解要介绍的「二分查找」的思想其实不是什么新鲜的事儿。如下图所示，它像极了「双指针」算法，left 和 right 向中间走，直到它们重合在一起。

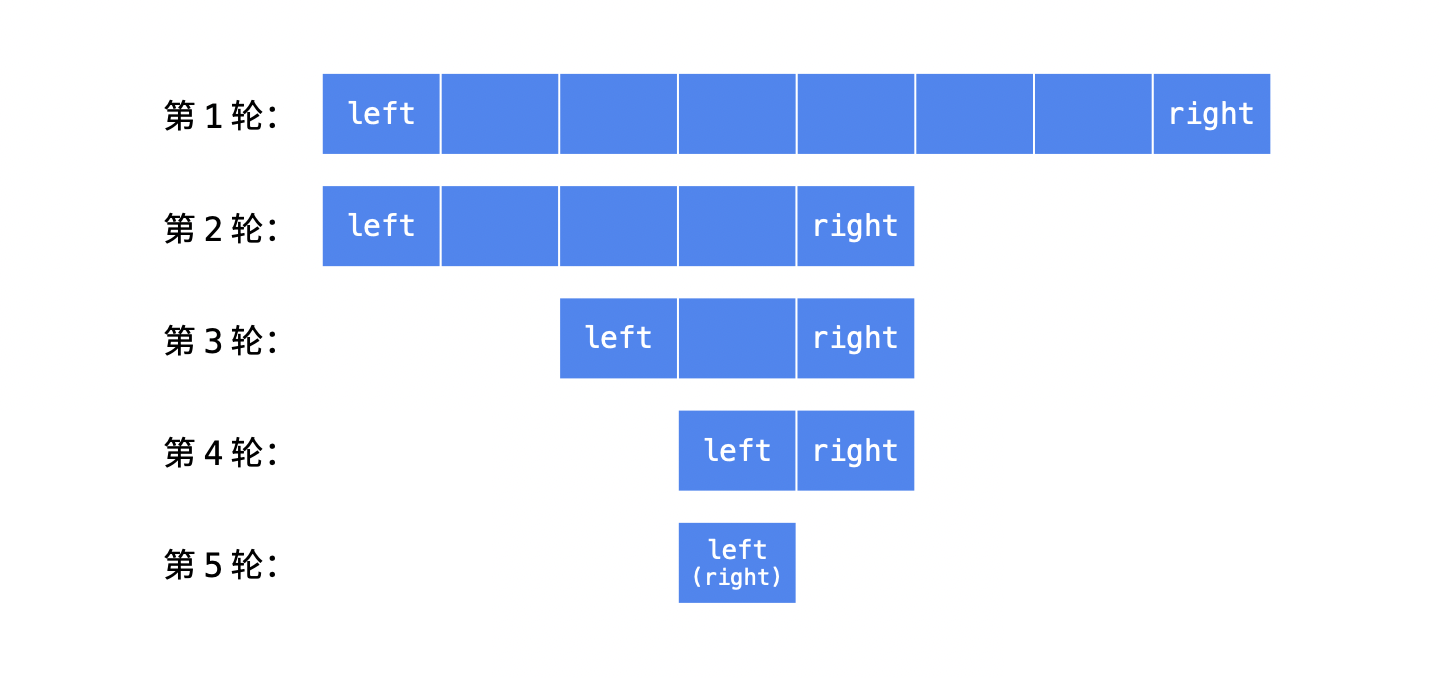
这种二分查找的思考路径，不是我发明的（「参考资料」在题解最后）。我一开始看到这种写法也觉得很惊讶，也搞不明白到底怎么回事，但是我看到的解释就只有「这是模板」，但没有看到为什么有这个模板。因此我 尝试去了解它，并使用它，然后整理成这篇题解。用这种二分查找的思路，可以解决「力扣」上 所有的 「二分查找」问题。