「力扣」第 69 题：x 的平方根（简单）

说明：本题解于 2021 年 4 月 3 日重写，精简了「二分查找」部分的描述，删去了「牛顿法」，关于「牛顿法」请见 「官方题解 (opens new window)」。

---

11111111

markdown content

() => {
  console.log('JavaScript code example')
}

markdown content

() => {
  console.log('Javascript code example')
}

本题是二分查找的典型应用场景：查找一个有确定范围的整数，根据 单调性 逐渐缩小搜索范围。

方法：二分查找

思路分析：

分析单调性：注意到题目中给出的例 2，小数部分将被舍去。我们就知道了，如果一个数 的平方大于 ，那么 一定不是 的平方根。我们下一轮需要在 区间里继续查找 的平方根。

参考代码：

public class Solution {

    public int mySqrt(int x) {
        // 特殊值判断
        if (x == 0) {
            return 0;
        }
        if (x == 1) {
            return 1;
        }

        int left = 1;
        int right = x / 2;
        // 在区间 [left..right] 查找目标元素
        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            // 注意：这里为了避免乘法溢出，改用除法
            if (mid > x / mid) {
                // 下一轮搜索区间是 [left..mid - 1]
                right = mid - 1;
            } else {
                // 下一轮搜索区间是 [mid..right]
                left = mid;
            }
        }
        return left;
    }
}

代码解释：

• 直觉上一个数的平方根一定不会超过它的一半，但是有特殊情况，因此解方程 ，得 。注意到：当 时，返回 ，当 时，返回 。因此只需要对 和 作单独判断。其它情况下，搜索的下界 ，上界 ；
• 使用 mid > x / mid 作为判断条件是因为 mid * mid > x 在 mid 很大的时候，mid * mid 有可能会整型溢出，使用 mid * mid > x 不能通过的测试用例如下：

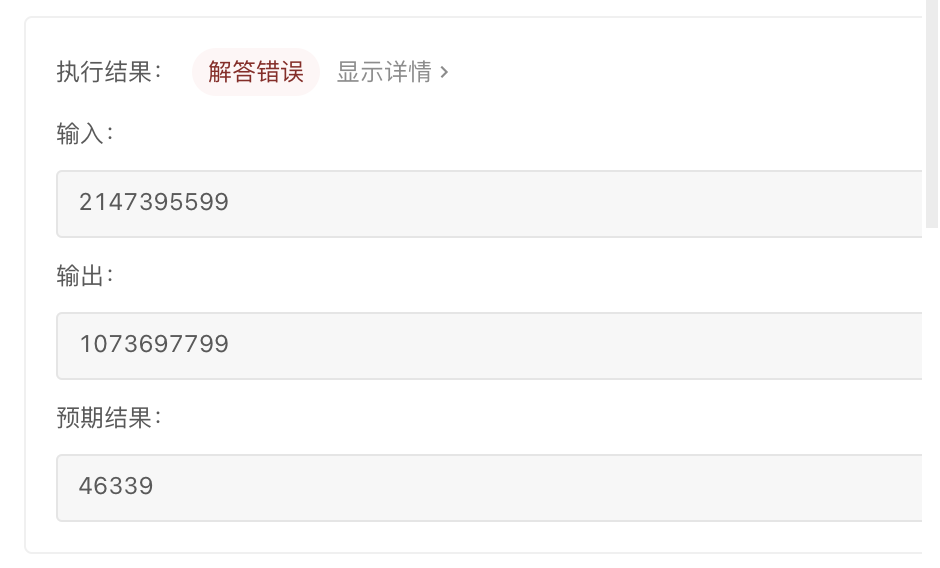{:style="width:400px"}{:align=center}

复杂度分析：

• 时间复杂度：，每一次搜索的区间大小为原来的 ，时间复杂度为 ；
• 空间复杂度：。

---

总结

1. 为什么用 while(left < right) 这种写法？

采用 while(left < right) 这种写法，在退出循环的时候有 left == right 成立，因此返回 left 或者 right 都可以。不用思考返回 left 还是 right。

2. 如何想到判断条件是 mid > x / mid？

while(left < right) 这种写法把区间分成两个区间，一个区间一定不存在目标元素，另一个区间有可能存在目标元素。因此 先思考满足什么条件的 mid 一定不是目标元素，进而思考下一轮搜索区间不容易出错，它的反面就是另一个区间。

根据本题解最开始分析例 2。我们分析出：如果一个数 的平方大于 ，那么 一定不是 的平方根，这种情况下，搜索区间是 （这里 a = mid，下同），这就是这种情况下我们将右边界设置为 right = mid - 1 的原因。剩下的情况不用思考，搜索区间一定是 ，此时设置 left = mid。

3. 取中间数为什么需要加 1？

这一点初学的时候很难理解（包括我自己），但其实我们只要对着错误的测试用例打印出相关变量看一下。

public class Solution {

    public int mySqrt(int x) {
        // 特殊值判断
        if (x == 0) {
            return 0;
        }
        if (x == 1) {
            return 1;
        }

        int left = 1;
        int right = x / 2;
        // 在区间 [left..right] 查找目标元素
        while (left < right) {
            // 取中间数 mid 下取整时
            int mid = left + (right - left ) / 2;

            // 调试语句开始
            try {
                Thread.sleep(1000);
            } catch (InterruptedException e) {
                e.printStackTrace();
            }
            System.out.println("left = " + left + ", right = " + right + ", mid = " + mid);
            // 调试语句结束

            // 注意：这里为了避免乘法溢出，改用除法
            if (mid > x / mid) {
                // 下一轮搜索区间是 [left..mid - 1]
                right = mid - 1;
            } else {
                // 下一轮搜索区间是 [mid..right]
                left = mid;
            }
        }
        return left;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int x = 9;
        int res = solution.mySqrt(x);
        System.out.println(res);
    }
}

控制台输出：

left = 1, right = 4, mid = 2
left = 2, right = 4, mid = 3
left = 3, right = 4, mid = 3
left = 3, right = 4, mid = 3
left = 3, right = 4, mid = 3
left = 3, right = 4, mid = 3

分析原因：在区间只有 个数的时候，根据 if、else 的逻辑区间的划分方式是：[left..mid - 1] 与 [mid..right]。如果 mid 下取整，在区间只有 个数的时候有 mid = left，一旦进入分支 [mid..right] 区间不会再缩小，发生死循环。

解决办法：把取中间数的方式成上取整。