LeetCode 第 88 题：“合并两个有序数组”题解

题解地址：思路没有创新的地方，主要提供逻辑清楚的代码和编码细节（Python 代码、Java 代码）。

说明：文本首发在力扣的题解版块，更新也会在第 1 时间在上面的网站中更新，这篇文章只是上面的文章的一个快照，您可以点击上面的链接看到其他网友对本文的评论。

给定两个有序整数数组 nums1 和 nums2，将 nums2 合并到 nums1 中，使得 num1 成为一个有序数组。

说明:

初始化 nums1 和 nums2 的元素数量分别为 m 和 n。你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。示例:

输入: nums1 = [1,2,3,0,0,0], m = 3 nums2 = [2,5,6], n = 3

输出: [1,2,2,3,5,6]

思路没有创新的地方，主要提供逻辑清楚的代码和编码细节（Python 代码、Java 代码）

思路分析：

合并两个有序数组是归并排序的子过程。学习过归并排序的朋友们，解决这个问题一定不在话下。

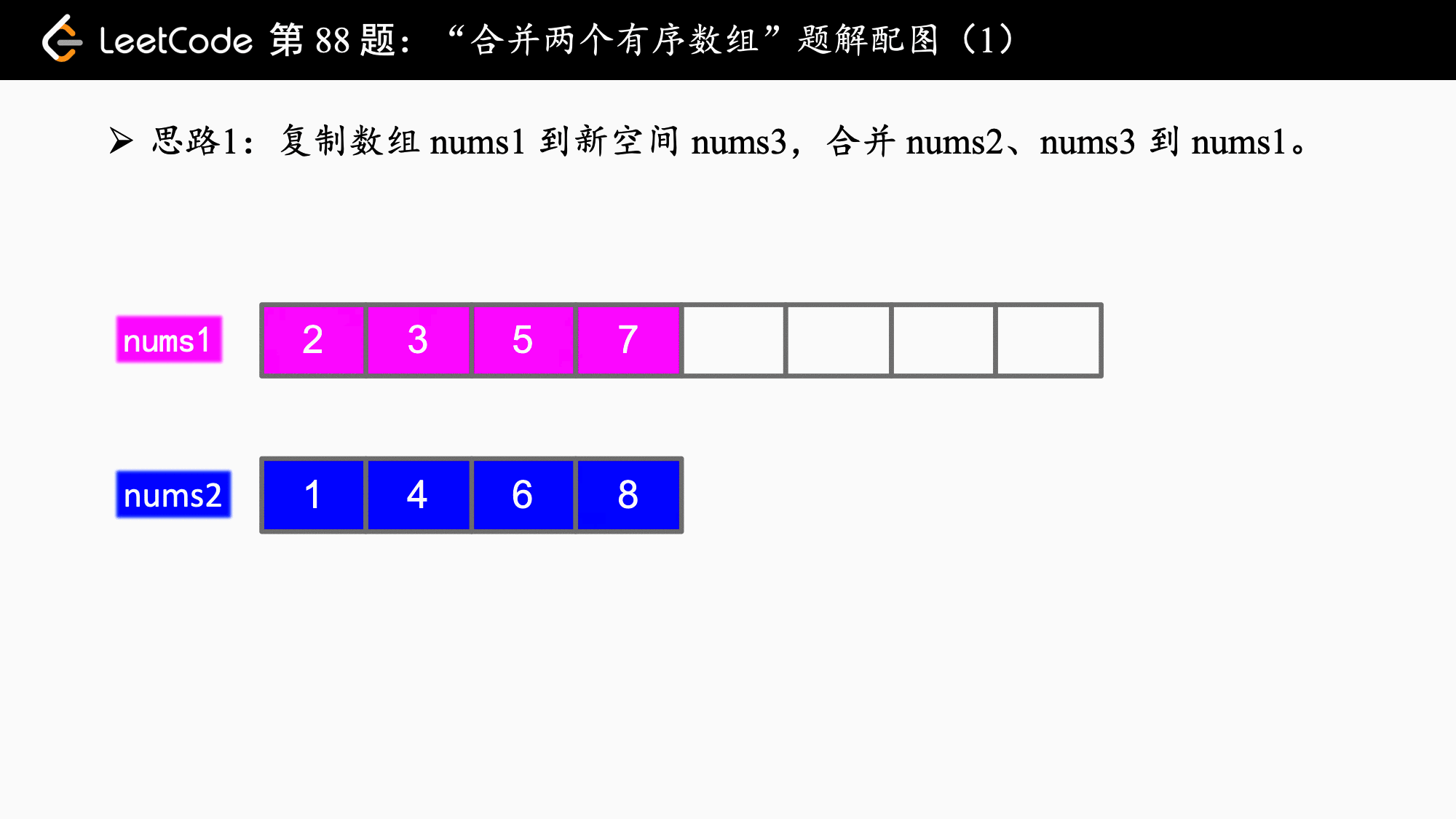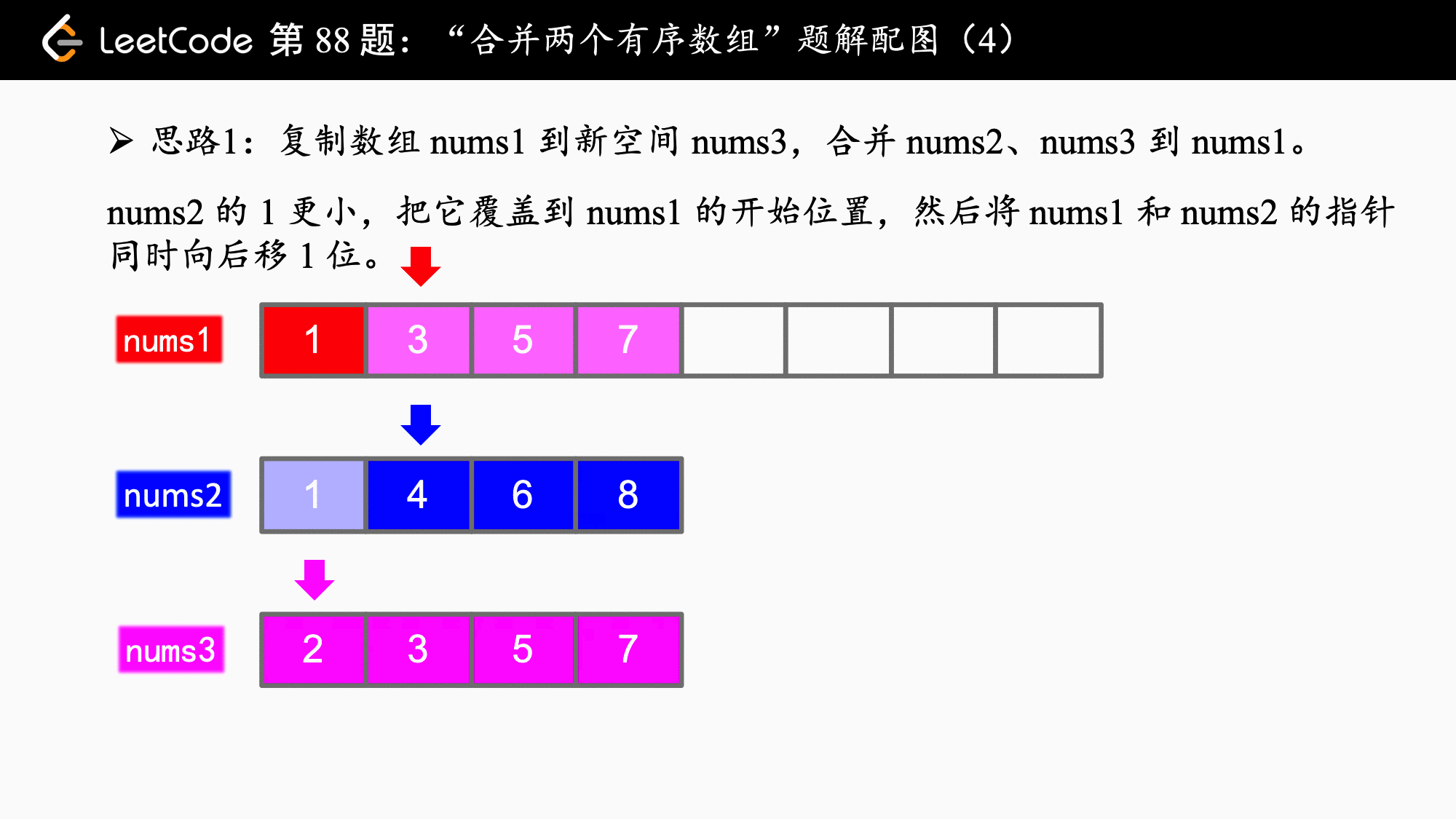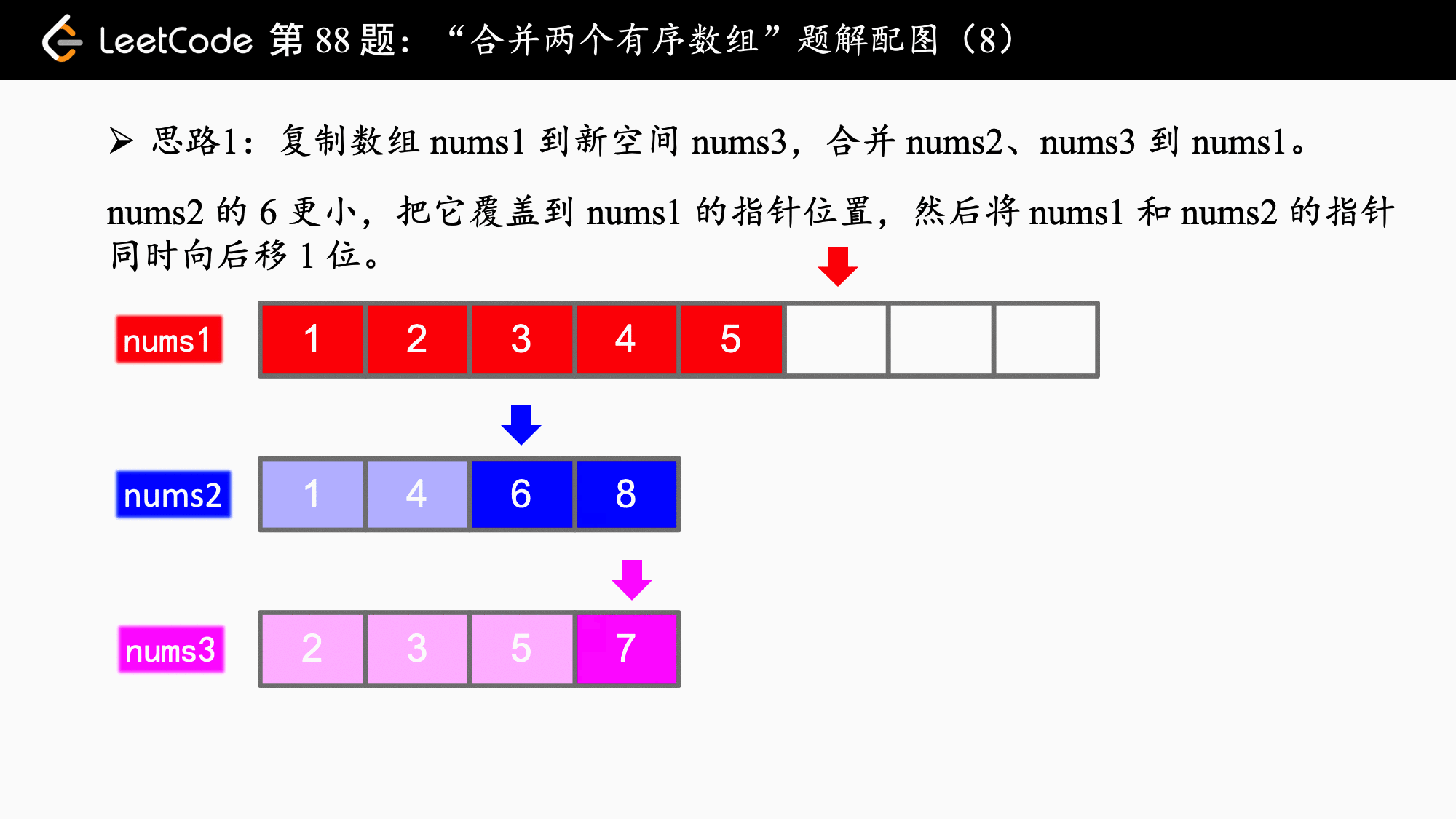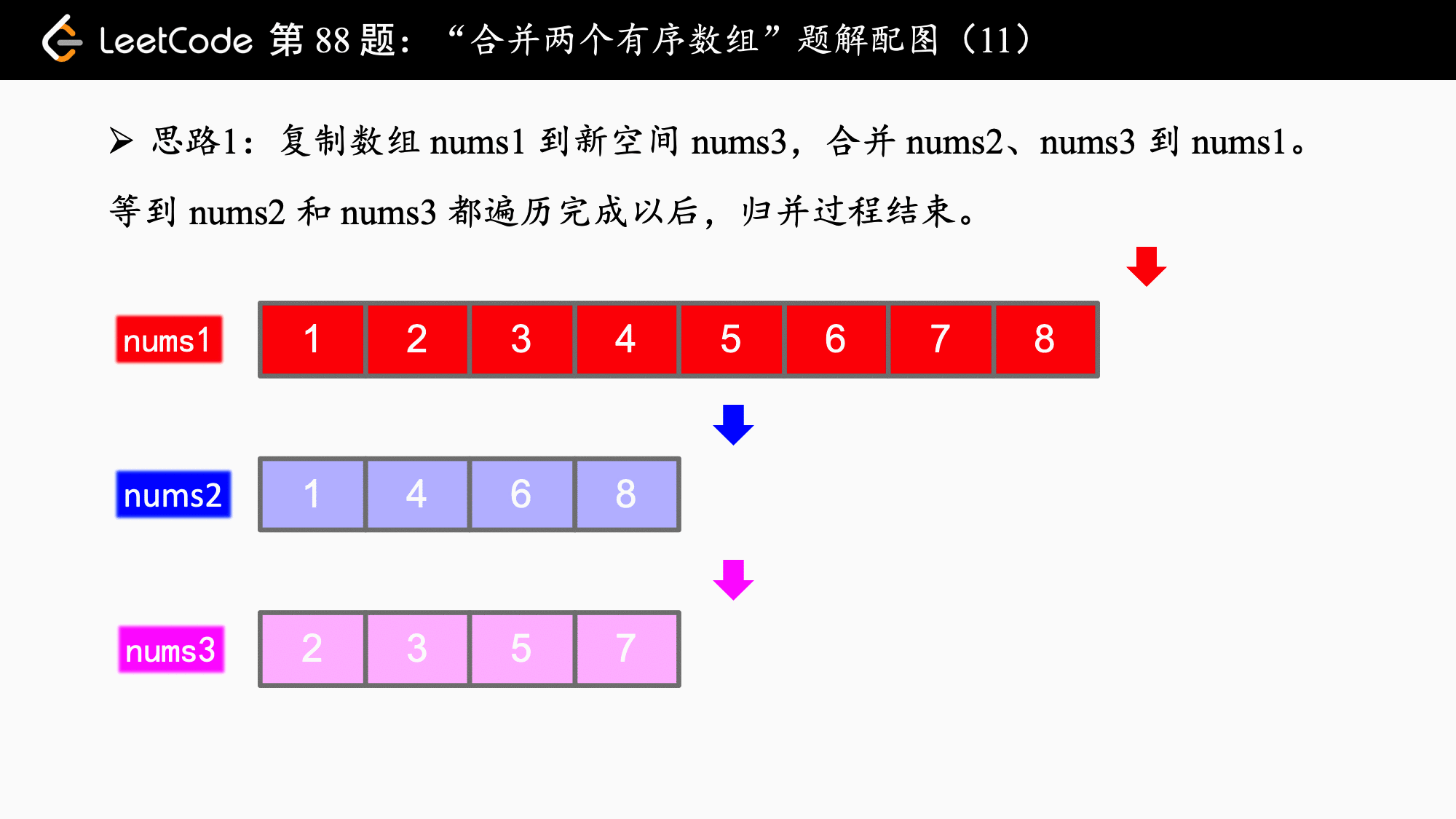
这道题的说明：

你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。

就暗示我们其实可以从后向前归并。

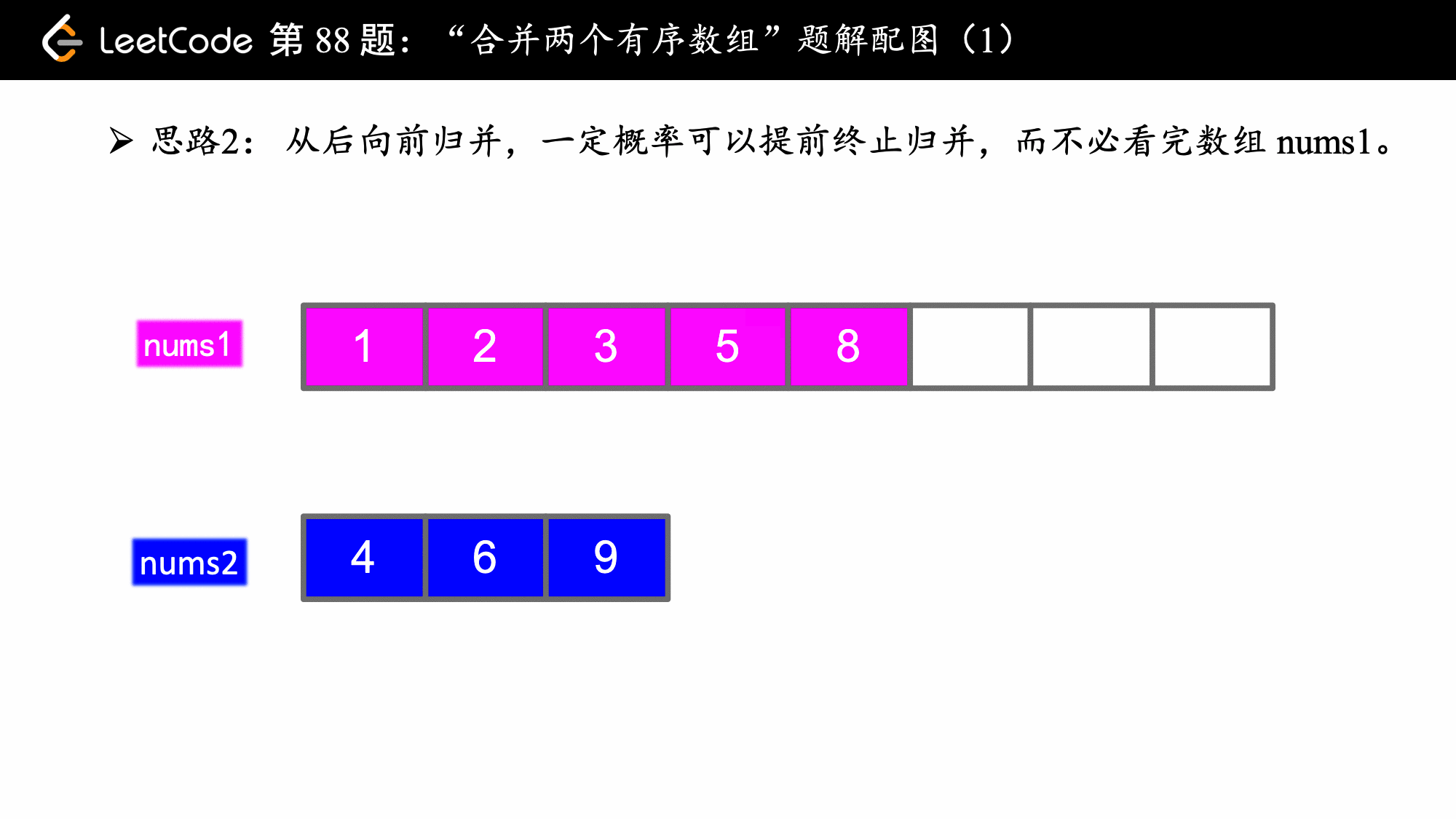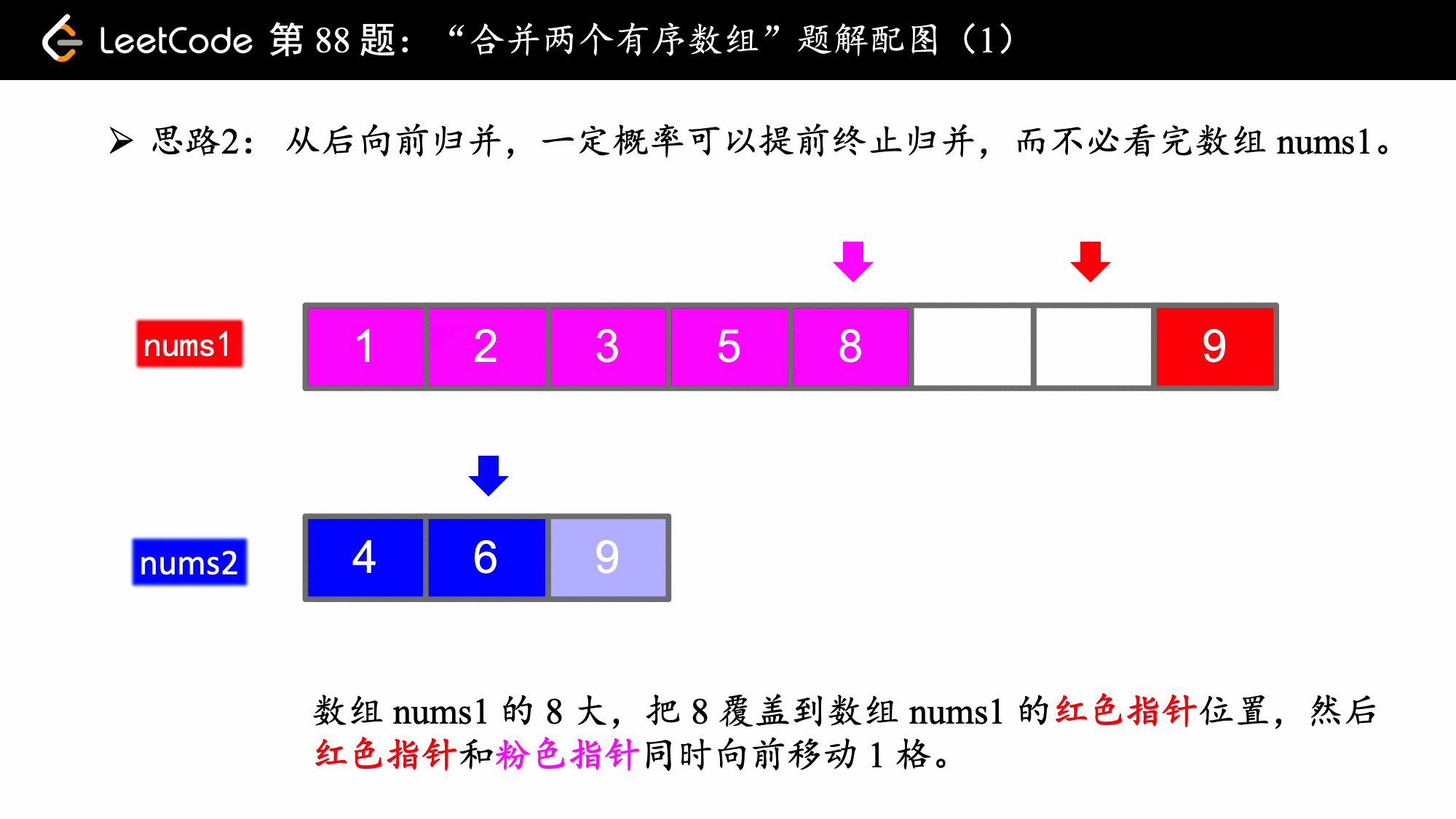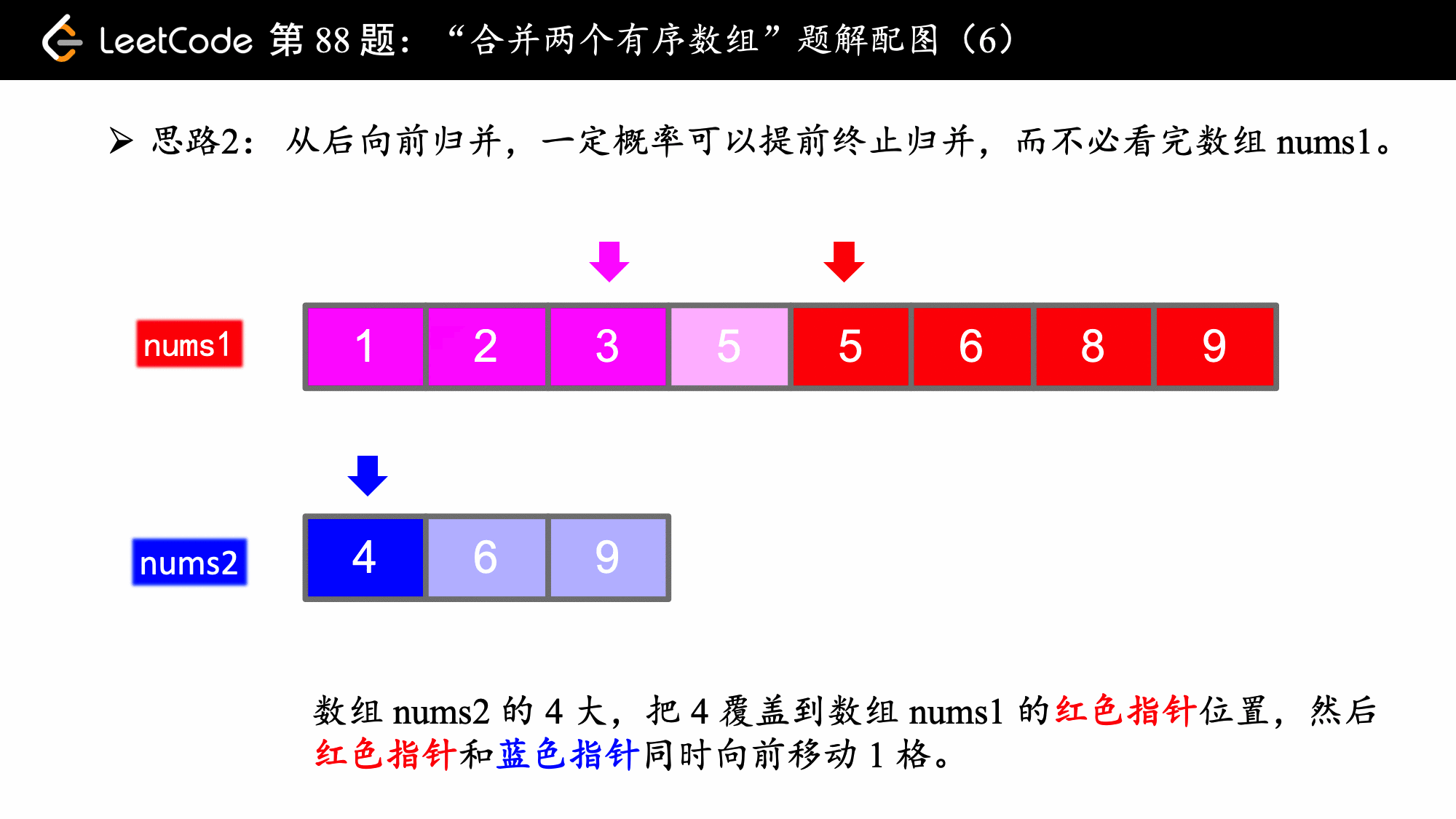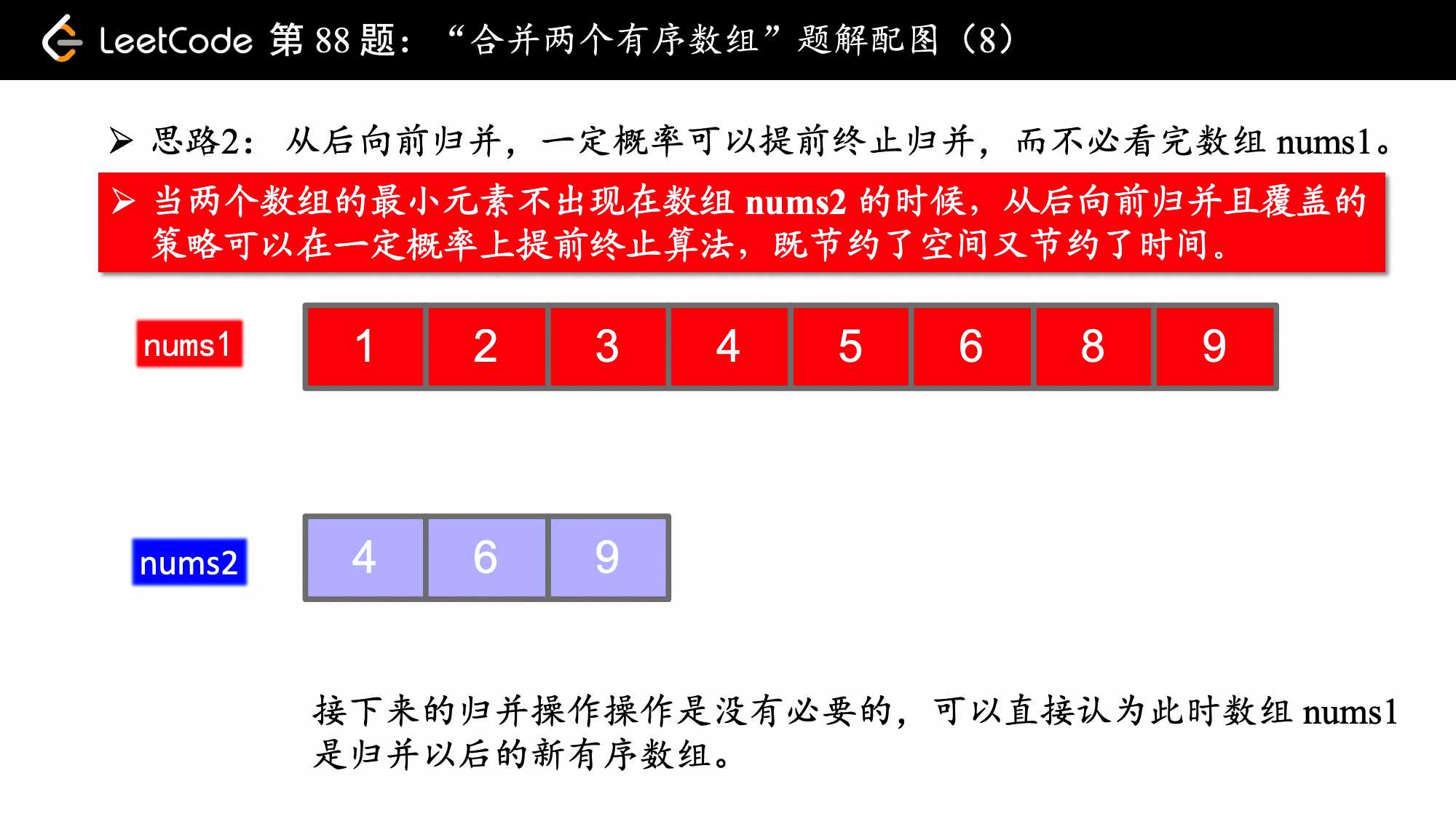
思想并不难，主要在编码上要注意一些细节。

编码细节：

下面的代码使用 for 循环表示我们一个一个确定归并以后的数；
在 for 循环内用 if elseif else 结构，保证一次只会执行一个分支；
为保证逻辑清晰，个人不建议写 nums[i++] 这样的代码，一行代码只执行一个逻辑，另外我看到 i++ 或者 ++i 脑子里还要先想一想，位于数组索引位置的时候到底是先加还是后加，我们不应该且没有必要给别人阅读代码造成理解上的一点点小麻烦，不过本人尊重任何个人的编码风格和习惯；
分支里面先写其中一个指针遍历完成的逻辑，否则会发生数组下标越界：把 i 先用完，j 先用完的逻辑写在开头是为了防止数组下标越界，这一点不论是从前向后归并还是从后向前归并来说都是一致的；
从后向前归并的时候，如果 nums2 数组用完了，可以直接结束算法，因为算法如果执行下去，也是数组 nums1 自己给自己赋值，还要执行相应的判断，没有必要。

方法一：从头到尾归并

参考代码 1：

Python 代码：

from typing import List


class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        # 只需要把 nums1 的有效个元素复制到 nums3 就可以了
        nums3 = nums1[:m]

        i = 0
        j = 0
        # 从前向后归并，比较 nums3 和 nums2 前端的元素哪个小，谁小谁出列，覆盖 nums1
        for k in range(m + n):
            # 注意：要把 nums3 和 nums2 归并完成的逻辑写在前面，否则会出现数组下标越界异常
            if i == m:
                nums1[k] = nums2[j]
                j += 1
            elif j == n:
                nums1[k] = nums3[i]
                i += 1
            elif nums3[i] < nums2[j]:
                nums1[k] = nums3[i]
                i += 1
            else:
                nums1[k] = nums2[j]
                j += 1

Java 代码：

public class Solution {

    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int[] nums3 = new int[m];
        // 只需要把 nums1 的有效个元素复制到 nums3 就可以了
        System.arraycopy(nums1, 0, nums3, 0, m);
        // 数组3
        int i = 0;
        // 数组2
        int j = 0;
        int length = m + n;
        // 从前向后归并，比较 nums3 和 nums2 前端的元素哪个小，谁小谁出列，覆盖 nums1
        for (int k = 0; k < length; k++) {
            // 注意：要把 nums3 和 nums2 归并完成的逻辑写在前面，否则会出现数组下标越界异常
            if (i == m) {
                nums1[k] = nums2[j];
                j++;
            } else if (j == n) {
                nums1[k] = nums3[i];
                i++;
            } else if (nums3[i] < nums2[j]) {
                nums1[k] = nums3[i];
                i++;
            } else {
                nums1[k] = nums2[j];
                j++;
            }
        }
    }
}

复杂度分析：

时间复杂度： $O(M + N)$ ，这里 $M$ 是数组 nums1 的长度， $N$ 是数组 nums2 的长度。
空间复杂度： $O(M)$ ，这里 $M$ 是 nums1 的长度。

方法二：从尾到头归并（更省空间，并且可以提前终止归并）

注意 1：从后向前归并，先写数组下标用完的逻辑，否则会出现数组下标异常；

注意 2：当 nums2 数组所有的数都看完的时候，算法终止。

参考代码 2：

Python 代码：

from typing import List


class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        i = m - 1
        j = n - 1
        # 从后向前归并，比较 nums1 和 nums2 末尾的元素哪个大，谁大谁出列，覆盖 nums1
        for k in range(m + n - 1, -1, -1):
            # 注意：同样要把 nums1 和 nums2 归并完成的逻辑写在前面，否则会出现数组下标越界异常
            if i == -1:
                # 这里直接把 nuns2 还没看的元素复制到 nums1 即可
                # 我们可以在循环中完成，在 Java 中有更好的方法
                nums1[k] = nums2[j]
                j -= 1
            elif j == -1:
                # 注意：这里直接 break 掉就可以了
                # 因为 nums2 遍历完成以后，nums1 剩下的元素虽然还没有看，但一定是排定以后的那个样子
                break
            elif nums1[i] > nums2[j]:
                nums1[k] = nums1[i]
                i -= 1
            else:
                nums1[k] = nums2[j]
                j -= 1

Java 代码：

import java.util.Arrays;

/**
 * 题目中说了，nums1 够用，我可以从后向前归并
 * 这道题真正想考查的应该是这种实现方式，我们不能太死板，按照教科书的方式从头归并
 * https://leetcode-cn.com/problems/merge-sorted-array/description/
 *
 * @author liwei
 */
public class Solution {

    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int len = m + n;
        int i = m - 1;
        int j = n - 1;
        // 从后向前归并，比较 nums1 和 nums2 末尾的元素哪个大，谁大谁出列，覆盖 nums1
        for (int k = len - 1; k >= 0; k--) {
            if (i == -1) {
                // 注意：同样要把 nums1 和 nums2 归并完成的逻辑写在前面，否则会出现数组下标越界异常
                // 此时 j 位于数组 nums2 的末尾索引位置，还未看的数组 nums2 的长度为 j + 1
                // 复制完 break 掉即可
                System.arraycopy(nums2, 0, nums1, 0, j + 1);
                break;
            } else if (j == -1) {
                // 注意：这里直接 break 掉就可以了
                // 因为 nums2 遍历完成以后，nums1 剩下的元素虽然还没有看，但一定是排定以后的那个样子
                break;
            } else if (nums1[i] >= nums2[j]) {
                // 谁大谁出列
                nums1[k] = nums1[i];
                i--;
            } else {
                assert nums1[i] < nums2[j];
                nums1[k] = nums2[j];
                j--;
            }
        }
    }

    public static void main(String[] args) {
        int[] nums1 = {1, 2, 3, 0, 0, 0};
        int m = 3;
        int[] nums2 = {2, 5, 6};
        int n = 3;
        Solution solution = new Solution();
        solution.merge(nums1, m, nums2, n);
        System.out.println(Arrays.toString(nums1));
    }
}

复杂度分析：

时间复杂度： $O(M + N)$ ，这里 $M$ 是数组 nums1 的长度， $N$ 是数组 nums2 的长度。
空间复杂度： $O(1)$ ，该算法没有使用额外的存储空间，仅使用了常数个临时变量用于比较。

← LeetCode 第 16 题：“最接近的三数之和”题解 LeetCode 第 167 题：“两数之和 II - 输入有序数组”题解 →

# LeetCode 第 88 题：“合并两个有序数组”题解

# 思路没有创新的地方，主要提供逻辑清楚的代码和编码细节（Python 代码、Java 代码）

# 方法一：从头到尾归并

# 方法二：从尾到头归并（更省空间，并且可以提前终止归并）

LeetCode 第 88 题：“合并两个有序数组”题解

思路没有创新的地方，主要提供逻辑清楚的代码和编码细节（Python 代码、Java 代码）

方法一：从头到尾归并

方法二：从尾到头归并（更省空间，并且可以提前终止归并）