LeetCode 第 210 题:“课程表 II”题解
题解地址:拓扑排序 + 深度优先遍历(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:210. 课程表 II。
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
示例 1:
输入: 2, [[1,0]] 输出: [0,1] 解释: 总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。 示例 2:
输入: 4, [[1,0],[2,0],[3,1],[3,2]] 输出: [0,1,2,3] or [0,2,1,3] 解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。 因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。 说明:
输入的先决条件是由边缘列表表示的图形,而不是邻接矩阵。详情请参见图的表示法。 你可以假定输入的先决条件中没有重复的边。 提示:
这个问题相当于查找一个循环是否存在于有向图中。如果存在循环,则不存在拓扑排序,因此不可能选取所有课程进行学习。 通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程(21分钟),介绍拓扑排序的基本概念。 拓扑排序也可以通过 BFS 完成。
拓扑排序 + 深度优先遍历(Python 代码、Java 代码)
这两种思路都可以完成 LeetCode 第 207 题。
方法一:拓扑排序(Kahn 算法)
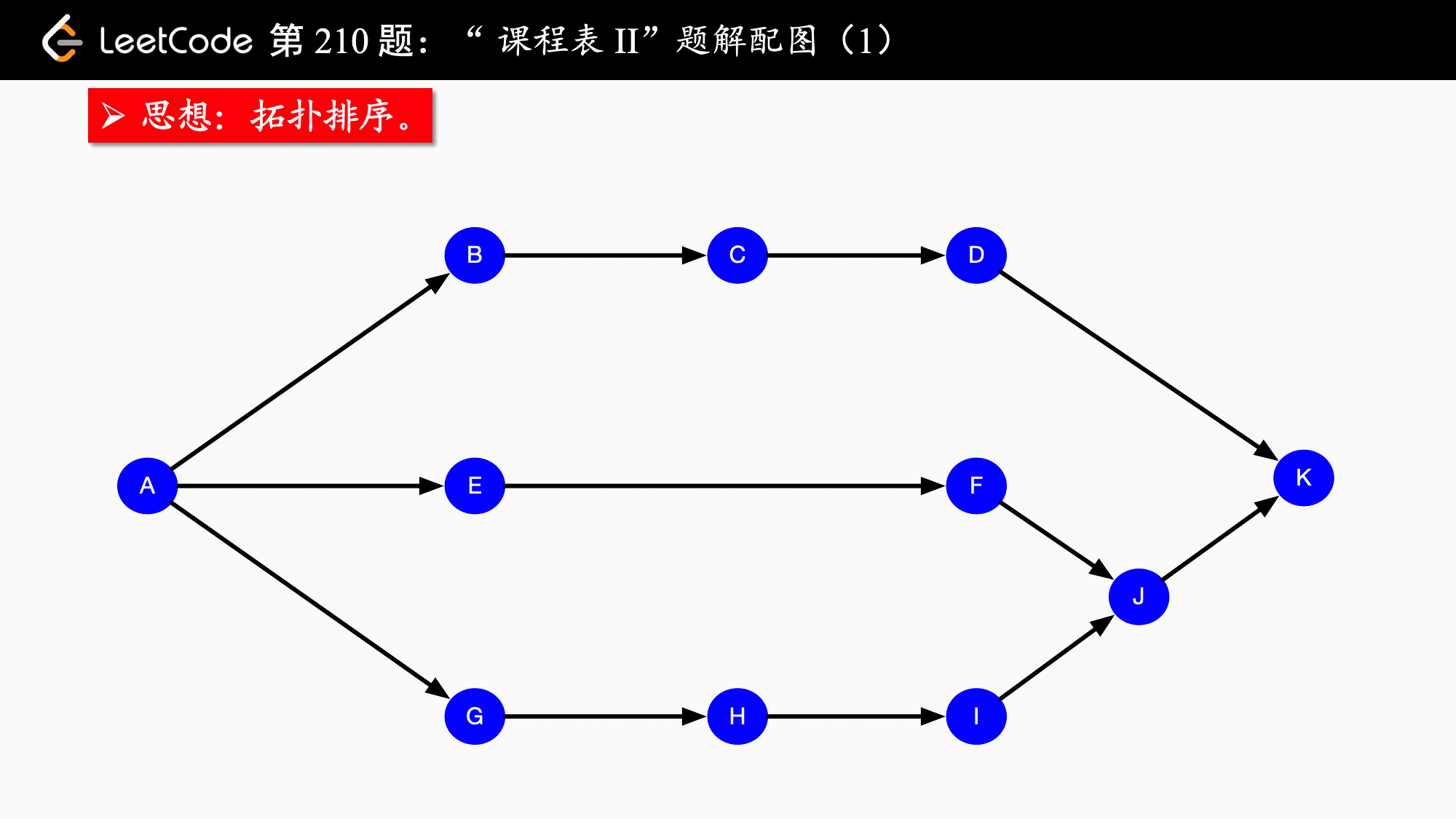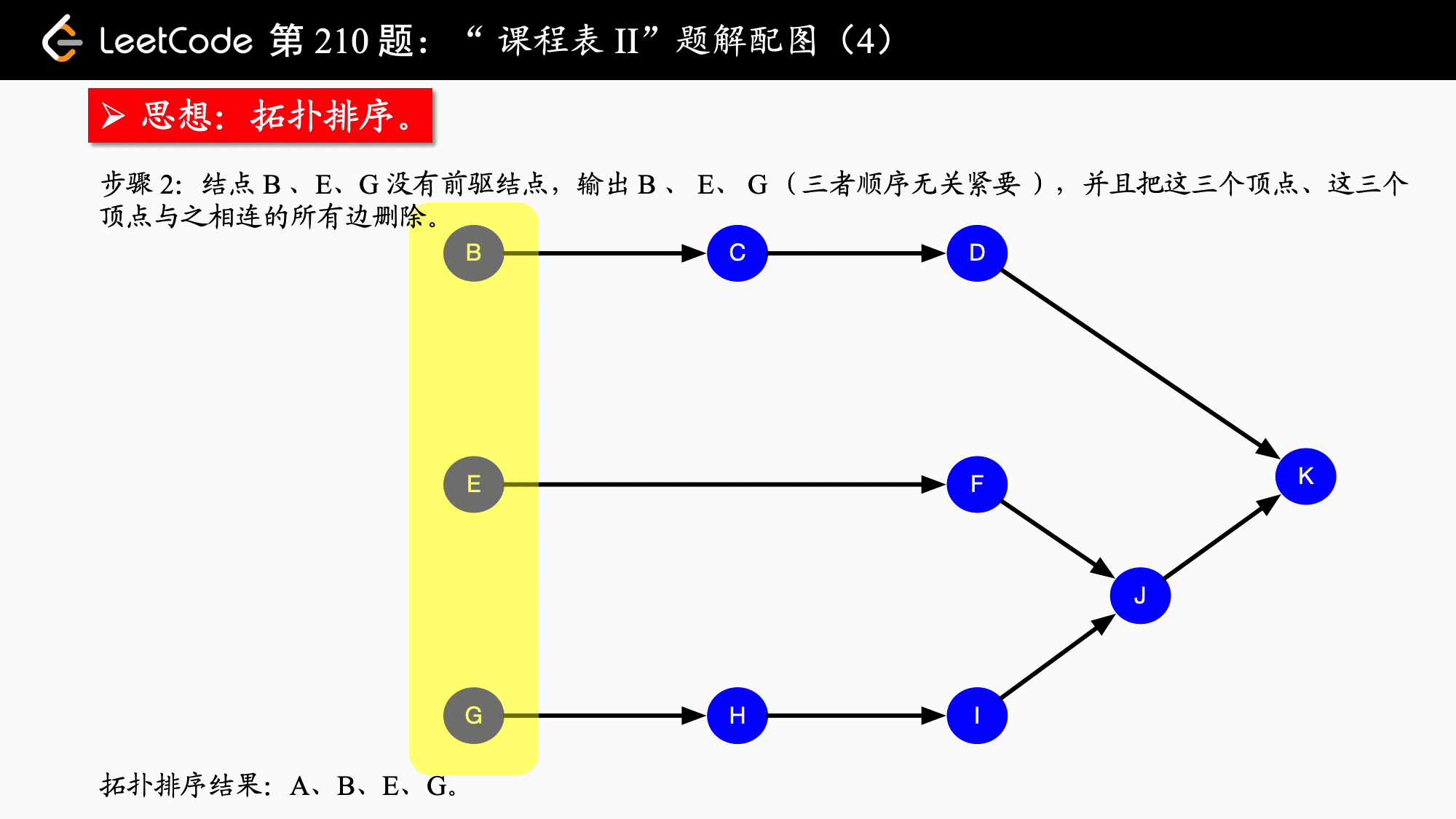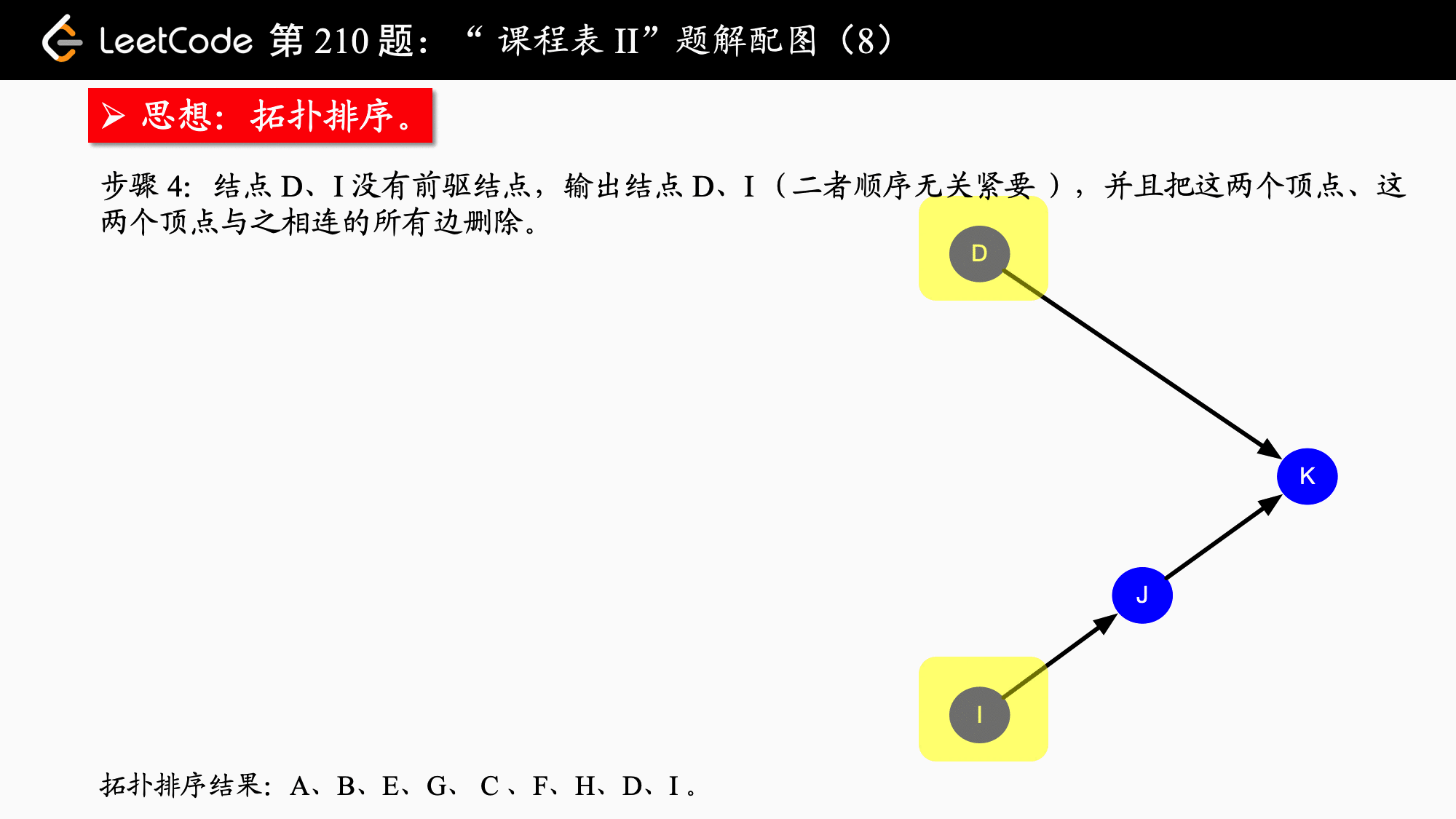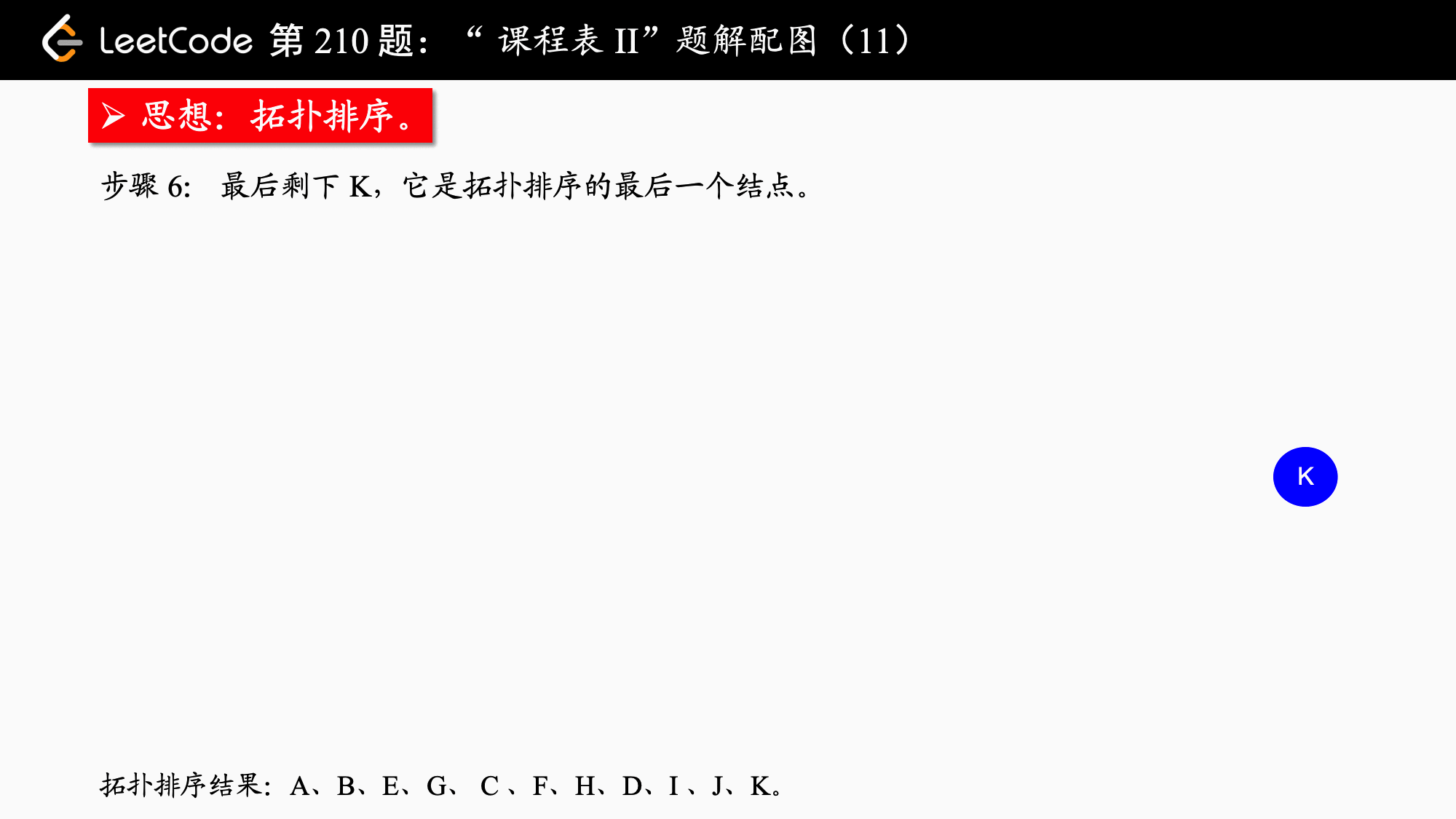
拓扑排序实际上应用的是贪心算法,贪心算法简而言之:每一步最优,则全局最优。具体到拓扑排序,每一次都输出入度为 的结点,并移除它、修改它指向的结点的入度,依次得到的结点序列就是拓扑排序的结点序列。如果图中还有结点没有被移除,则说明“不能完成所有课程的学习”。
拓扑排序保证了每个活动(在这题中是“课程”)的所有前驱活动都排在该活动的前面,并且可以完成所有活动。拓扑排序的结果不唯一。拓扑排序还可以用于检测一个有向图是否有环。相关的概念还有 AOV 网,这里就不展开了。
算法流程:
1、在开始排序前,扫描对应的存储空间(使用邻接表),将入度为 的结点放入队列。
2、只要队列非空,就从队首取出入度为 的结点,将这个结点输出到结果集中,并且将这个结点的所有邻接结点(它指向的结点)的入度减 ,在减 以后,如果这个被减 的结点的入度为 ,就继续入队。
3、当队列为空的时候,检查结果集中的顶点个数是否和课程数相等即可。
(思考这里为什么要使用队列?如果不用队列,还可以怎么做,会比用队列的效果差还是更好?)
在代码具体实现的时候,除了保存入度为 的队列,我们还需要两个辅助的数据结构:
1、邻接表:通过结点的索引,我们能够得到这个结点的后继结点;
2、入度数组:通过结点的索引,我们能够得到指向这个结点的结点个数。
这个两个数据结构在遍历题目给出的邻边以后就可以很方便地得到。
参考代码 1:
Python 代码:
class Solution(object):
def findOrder(self, numCourses, prerequisites):
"""
:type numCourses: int 课程门数
:type prerequisites: List[List[int]] 课程与课程之间的关系
:rtype: bool
"""
# 课程的长度
clen = len(prerequisites)
if clen == 0:
# 没有课程,当然可以完成课程的学习
return [i for i in range(numCourses)]
# 入度数组,一开始全部为 0
in_degrees = [0 for _ in range(numCourses)]
# 邻接表
adj = [set() for _ in range(numCourses)]
# 想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
# 1 -> 0,这里要注意:不要弄反了
for second, first in prerequisites:
in_degrees[second] += 1
adj[first].add(second)
# print("in_degrees", in_degrees)
# 首先遍历一遍,把所有入度为 0 的结点加入队列
res = []
queue = []
for i in range(numCourses):
if in_degrees[i] == 0:
queue.append(i)
while queue:
top = queue.pop(0)
res.append(top)
for successor in adj[top]:
in_degrees[successor] -= 1
if in_degrees[successor] == 0:
queue.append(successor)
if len(res) != numCourses:
return []
return res
Java 代码:
import java.util.ArrayList;
import java.util.HashSet;
import java.util.LinkedList;
/**
* 使用拓扑排序来完成
*
* @author liwei
* @date 18/6/24 下午3:11
*/
public class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
// 先处理极端情况
if (numCourses <= 0) {
return new int[0];
}
// 邻接表表示
HashSet<Integer>[] graph = new HashSet[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new HashSet<>();
}
// 入度表
int[] inDegree = new int[numCourses];
// 遍历 prerequisites 的时候,把 邻接表 和 入度表 都填上
for (int[] p : prerequisites) {
graph[p[1]].add(p[0]);
inDegree[p[0]]++;
}
LinkedList<Integer> queue = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (inDegree[i] == 0) {
queue.addLast(i);
}
}
ArrayList<Integer> res = new ArrayList<>();
while (!queue.isEmpty()) {
// 当前入度为 0 的结点
Integer inDegreeNode = queue.removeFirst();
// 加入结果集中
res.add(inDegreeNode);
// 下面从图中删去
// 得到所有的后继课程,接下来把它们的入度全部减去 1
HashSet<Integer> nextCourses = graph[inDegreeNode];
for (Integer nextCourse : nextCourses) {
inDegree[nextCourse]--;
// 马上检测该结点的入度是否为 0,如果为 0,马上加入队列
if (inDegree[nextCourse] == 0) {
queue.addLast(nextCourse);
}
}
}
// 如果结果集中的数量不等于结点的数量,就不能完成课程任务,这一点是拓扑排序的结论
int resLen = res.size();
if (resLen == numCourses) {
int[] ret = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
ret[i] = res.get(i);
}
return ret;
} else {
return new int[0];
}
}
}
复杂度分析:
- 时间复杂度:。这里 表示邻边的条数, 表示结点的个数。初始化入度为 的集合需要遍历整张图,具体做法是检查每个结点和每条边,因此复杂度为 ,然后对该集合进行操作,又需要遍历整张图中的每个结点和每条边,复杂度也为 ;
- 空间复杂度::入度数组、邻接表的长度都是结点的个数 ,即使使用队列,队列最长的时候也不会超过 ,因此空间复杂度是 。
方法二:深度优先遍历
这里要使用逆邻接表。其实就是检测这个有向图中有没有环,只要存在环,这些课程就不能按要求学完。
算法流程:
第 1 步:构建逆邻接表;
第 2 步:递归处理每一个还没有被访问的结点,具体做法很简单:对于一个结点来说,先输出指向它的所有顶点,再输出自己。
第 3 步:如果这个顶点还没有被遍历过,就递归遍历它,把所有指向它的结点都输出了,再输出自己。注意:当访问一个结点的时候,应当先递归访问它的前驱结点,直至前驱结点没有前驱结点为止。
参考代码 2:
Python 代码:
class Solution(object):
def findOrder(self, numCourses, prerequisites):
"""
:type numCourses: int 课程门数
:type prerequisites: List[List[int]] 课程与课程之间的关系
:rtype: bool
"""
# 课程的长度
clen = len(prerequisites)
if clen == 0:
# 没有课程,当然可以完成课程的学习
return [i for i in range(numCourses)]
# 逆邻接表
inverse_adj = [set() for _ in range(numCourses)]
# 想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
# 1 -> 0,这里要注意:不要弄反了
for second, first in prerequisites:
inverse_adj[second].add(first)
visited = [0 for _ in range(numCourses)]
# print("in_degrees", in_degrees)
# 首先遍历一遍,把所有入度为 0 的结点加入队列
res = []
for i in range(numCourses):
if self.__dfs(i,inverse_adj, visited, res):
return []
return res
def __dfs(self, vertex, inverse_adj, visited, res):
"""
注意:这个递归方法的返回值是返回是否有环
:param vertex: 结点的索引
:param inverse_adj: 逆邻接表,记录的是当前结点的前驱结点的集合
:param visited: 记录了结点是否被访问过,2 表示当前正在 DFS 这个结点
:return: 是否有环
"""
# 2 表示这个结点正在访问
if visited[vertex] == 2:
# DFS 的时候如果遇到一样的结点,就表示图中有环,课程任务便不能完成
return True
if visited[vertex] == 1:
return False
# 表示正在访问这个结点
visited[vertex] = 2
# 递归访问前驱结点
for precursor in inverse_adj[vertex]:
# 如果没有环,就返回 False,
# 执行以后,逆拓扑序列就存在 res 中
if self.__dfs(precursor, inverse_adj, visited, res):
return True
# 能走到这里,说明所有的前驱结点都访问完了,所以可以输出了
# 并且将这个结点状态置为 1
visited[vertex] = 1
# 先把 vertex 这个结点的所有前驱结点都输出之后,再输出自己
res.append(vertex)
# 最后不要忘记返回 False 表示无环
return False
Java 代码:
import java.util.HashSet;
import java.util.Stack;
/**
* @author liwei
* @date 18/6/24 下午4:10
*/
public class Solution3 {
/**
* @param numCourses
* @param prerequisites
* @return
*/
public int[] findOrder(int numCourses, int[][] prerequisites) {
if (numCourses <= 0) {
// 连课程数目都没有,就根本没有办法完成练习了,根据题意应该返回空数组
return new int[0];
}
int plen = prerequisites.length;
if (plen == 0) {
// 没有有向边,则表示不存在课程依赖,任务一定可以完成
int[] ret = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
ret[i] = i;
}
return ret;
}
int[] marked = new int[numCourses];
// 初始化有向图 begin
HashSet<Integer>[] graph = new HashSet[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new HashSet<>();
}
// 初始化有向图 end
// 有向图的 key 是前驱结点,value 是后继结点的集合
for (int[] p : prerequisites) {
graph[p[1]].add(p[0]);
}
// 使用 Stack 或者 List 记录递归的顺序,这里使用 Stack
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < numCourses; i++) {
if (dfs(i, graph, marked, stack)) {
// 注意方法的语义,如果图中存在环,表示课程任务不能完成,应该返回空数组
return new int[0];
}
}
// 在遍历的过程中,一直 dfs 都没有遇到已经重复访问的结点,就表示有向图中没有环
// 所有课程任务可以完成,应该返回 true
// 下面这个断言一定成立,这是拓扑排序告诉我们的结论
assert stack.size() == numCourses;
int[] ret = new int[numCourses];
// 想想要怎么得到结论,我们的 dfs 是一致将后继结点进行 dfs 的
// 所以压在栈底的元素,一定是那个没有后继课程的结点
// 那个没有前驱的课程,一定在栈顶,所以课程学习的顺序就应该是从栈顶到栈底
// 依次出栈就好了
for (int i = 0; i < numCourses; i++) {
ret[i] = stack.pop();
}
return ret;
}
/**
* 注意这个 dfs 方法的语义
*
* @param i 当前访问的课程结点
* @param graph
* @param marked 如果 == 1 表示正在访问中,如果 == 2 表示已经访问完了
* @return true 表示图中存在环,false 表示访问过了,不用再访问了
*/
private boolean dfs(int i,
HashSet<Integer>[] graph,
int[] marked,
Stack<Integer> stack) {
// 如果访问过了,就不用再访问了
if (marked[i] == 1) {
// 从正在访问中,到正在访问中,表示遇到了环
return true;
}
if (marked[i] == 2) {
// 表示在访问的过程中没有遇到环,这个节点访问过了
return false;
}
// 走到这里,是因为初始化呢,此时 marked[i] == 0
// 表示正在访问中
marked[i] = 1;
// 后继结点的集合
HashSet<Integer> successorNodes = graph[i];
for (Integer successor : successorNodes) {
if (dfs(successor, graph, marked, stack)) {
// 层层递归返回 true ,表示图中存在环
return true;
}
}
// i 的所有后继结点都访问完了,都没有存在环,则这个结点就可以被标记为已经访问结束
// 状态设置为 2
marked[i] = 2;
stack.add(i);
// false 表示图中不存在环
return false;
}
}
复杂度分析:
- 时间复杂度:;
- 空间复杂度:。