LeetCode 第 239 题:“滑动窗口的最大值”题解
题解地址:最大索引堆 + 双端队列存索引值的思路分析(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:239. 滑动窗口最大值。
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字。滑动窗口每次只向右移动一位。
返回滑动窗口最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3 输出: [3,3,5,5,6,7] 解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7 注意:
你可以假设 k 总是有效的,1 ≤ k ≤ 输入数组的大小,且输入数组不为空。
进阶:
你能在线性时间复杂度内解决此题吗?
最大索引堆 + 双端队列存索引值的思路分析(Python 代码、Java 代码)
这道问题最直接的想法就是“通过切片操作得到滑动窗口”,“切片”是 Python 中的一个操作,即截取一个序列,可以是字符串也可以是列表,中的连续子序列,再从中得到最大值,这是暴力解法。
动态得到“滑动窗口”的最大值,有一个数据结构是容易想到的,那就是“堆”(“优先队列”),特别地,应该使用“索引堆”。
根据「力扣」第 155 题:最小栈这个问题的思路,我们想到需要一个辅助的数据结构,当“滑动窗口”在移动的时候,我们直接看这个数据结构,就可以很快知道此时“滑动窗口”的最大值。
面试的时候,写“双端队列”,我肯定两个思路都回答。不写“索引堆”是因为代码量太多,并且“堆”我是写过很多遍,但是还是会写不好的,更别说“索引堆”了。
“双端队列存索引值”是我参考了众多优秀的题解之后总结出来的,希望我能够解释出使用“双端队列”的合理性。在编写本题解的过程中,由于要解释大佬们是如何想到“双端队列”的,我又想到了“索引堆”,以前学习“索引堆”的时候被这个东西“折磨”过,所以印象比较深,不过我个人觉得“索引堆”的思想更自然直接。
方法一:双端队列存索引值
如果不使用“索引堆”要定位要更新的元素的索引,还是有一定技巧的,当然挖掘题目中的已知条件可以帮助我们找到解决方案。
(1)根据「力扣」第 155 题:最小栈这个问题的思路,我们想到需要一个辅助的数据结构,当“滑动窗口”在移动的时候,我们直接看这个数据结构,就可以很快知道此时“滑动窗口”的最大值;
下面这一点是很关键的!
如果“当前考虑的数”比之前来的数还要大,那么之前的数(如果还没有划出“滑动窗口”)就一定不会是“滑动窗口”的最大值,应该把它们移除,因为它们“永远不会有出头之日”。
(2)根据上面的分析,之前的数离开,后来的数加进来,感觉这个数据结构可能是“队列”,但是之前可能还有的数比“当前考虑的数”还要大,还不能出“队列”,感觉这个数据结构还有可能是“栈”(不好意思,又把你绕晕了,不妨先看后面)。又感觉是“队列”,又感觉是“栈”的,我们先停一下,还有一个问题没有解决:左边界出“滑动窗口”的时候怎么办?。
(3)“左边界出滑动窗口的时候”只有 1 种情况需要考虑,那就是:
左边界恰好就是上一轮循环的滑动窗口的最大值,在这一轮“滑动窗口”右移,它必须被移出。
“左边界出滑动窗口”,左边界一定比当前考虑的数先进这个辅助的数据结构, 再结合 3(2),我们可以分析出这个辅助的数据结构即要是队列(先进先出),也要是栈(后进先出),因此“双端队列”是首选,因为要检测到左边界移除,左边界的索引很重要,知道索引也就知道了具体的值,因此“双端队列”里存的应该是数组的索引。
参考代码 1:“滑动窗口”存放的是数组的索引值。
Python 代码:
from typing import List
from collections import deque
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
size = len(nums)
# 特判
if size == 0:
return []
# 结果集
res = []
# 滑动窗口,注意:保存的是索引值
window = deque()
for i in range(size):
# 当元素从左边界滑出的时候,如果它恰恰好是滑动窗口的最大值
# 那么将它弹出
if i >= k and i - k == window[0]:
window.popleft()
# 如果滑动窗口非空,新进来的数比队列里已经存在的数还要大
# 则说明已经存在数一定不会是滑动窗口的最大值(它们毫无出头之日)
# 将它们弹出
while window and nums[window[-1]] <= nums[i]:
window.pop()
window.append(i)
# 队首一定是滑动窗口的最大值的索引
if i >= k - 1:
res.append(nums[window[0]])
return res
Java 代码:
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
public class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int len = nums.length;
// 特判
if (len == 0) {
return new int[]{};
}
// 结果集
List<Integer> res = new ArrayList<>();
// 滑动窗口,注意:保存的是索引值
ArrayDeque<Integer> deque = new ArrayDeque<>(k);
for (int i = 0; i < len; i++) {
// 当元素从左边界滑出的时候,如果它恰恰好是滑动窗口的最大值
// 那么将它弹出
if (i >= k && i - k == deque.getFirst()) {
deque.pollFirst();
}
// 如果滑动窗口非空,新进来的数比队列里已经存在的数还要大
// 则说明已经存在数一定不会是滑动窗口的最大值(它们毫无出头之日)
// 将它们弹出
while (!deque.isEmpty() && nums[deque.peekLast()] <= nums[i]) {
deque.pollLast();
}
deque.add(i);
// 队首一定是滑动窗口的最大值的索引
if (i >= k - 1) {
res.add(nums[deque.peekFirst()]);
}
}
int size = res.size();
int[] result = new int[size];
for (int i = 0; i < size; i++) {
result[i] = res.get(i);
}
return result;
}
}
方法二:使用最大索引堆
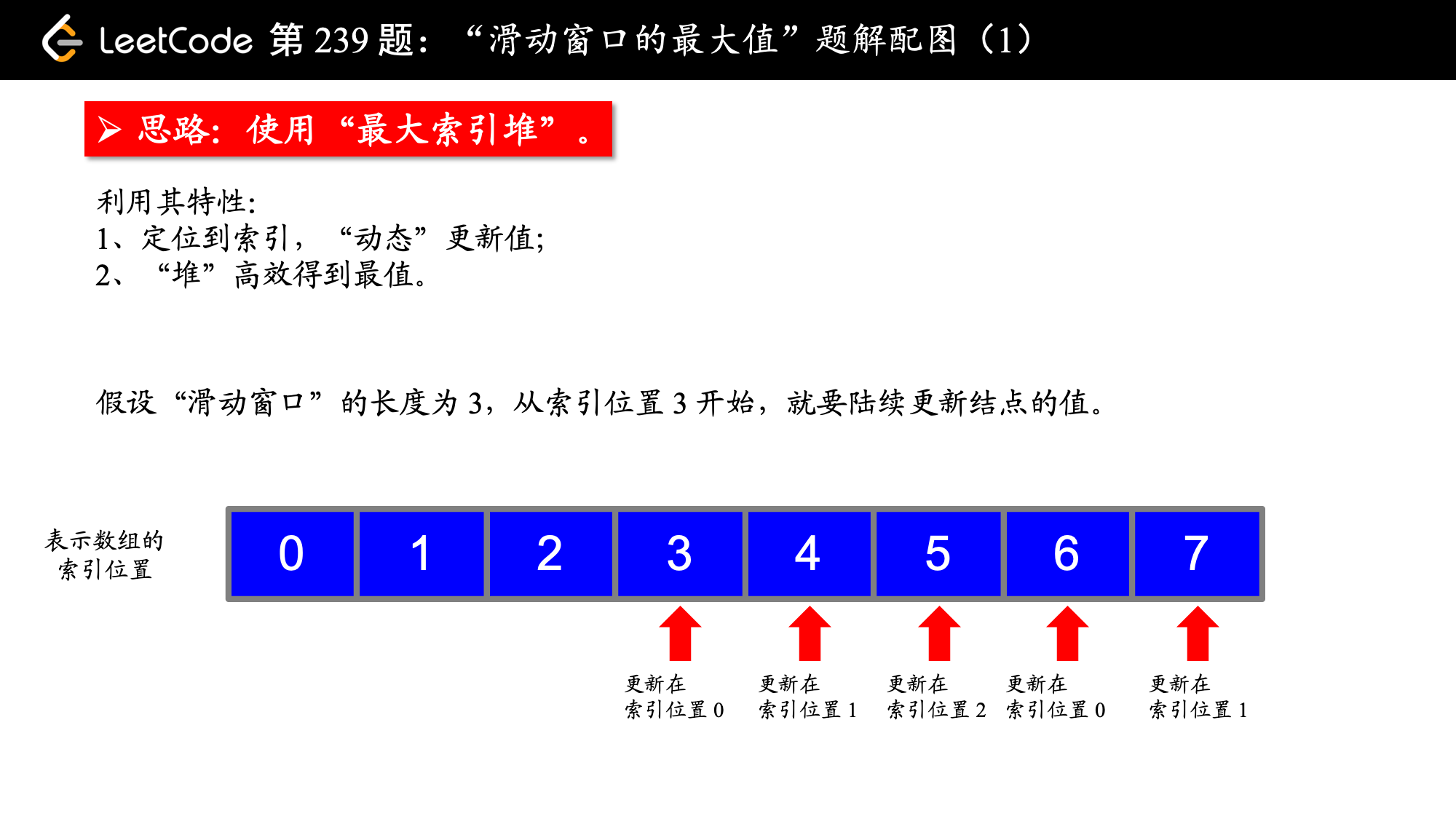
动态得到“滑动窗口”的最大值,有一个数据结构是容易想到的,那就是“堆”(“优先队列”),但是问题来了。当“滑动窗口”要把左边界移除的时候,我们虽然左边界是哪个元素,但是没有从一个堆中移除非最堆顶元素的操作,于是我就想“索引堆”可不可以呢?找到即将要滑出边界的那个索引,更新一下它的值就好,那么索引值如何更新呢?在纸上写一写,你就会发现规律:新进来的那个数的索引,把自己这个索引对 取模的那个索引更新一下就好了。
使用“索引堆”的原因:“索引堆”有一个更新操作,可以针对某个索引更新它的值,然后索引发生调整,使得索引数组组成最大堆。因为能方便地定位到某个元素,因此可以在新进来一个数的时候,使用更新操作,把马上要出“滑动窗口”的那个索引位置上的值更新成新进来的这个数的值就可以了(说起来很拗口,看代码会简洁很多)。
不过很纠结的是 Python 和 Java 都没有现成的“索引堆”,需要自己编写,请见“参考代码 2”。
- 对“索引堆”感兴趣的朋友,可以参考我的学习笔记《【算法日积月累】11-索引堆》,注意文中提到的“索引数组”和“反向查找”技巧是值得借鉴的,文后还给出了示例代码和参考资料。
参考代码 2:“最大索引堆”得自己写,正好就利用了 LeetCode 的测试用例检验一下自己有没有写对。
Python 代码:
from typing import List
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
size = len(nums)
# 特判
if size == 0:
return []
# 初始化最大索引堆,其容量是滑动窗口的大小
index_max_heap = Solution.IndexMaxHeap(k)
# 首先先把前 k 个元素加进去
for i in range(k):
index_max_heap.insert(i, nums[i])
# 结果集
res = []
# 然后就是产生滑动窗口的过程,先输出最大值,
# 而后把当前考虑的数插入到将要滑出的左边界的索引位置
for i in range(k, size):
res.append(index_max_heap.peek_max_value())
index_max_heap.change(i % k, nums[i])
# 因为最大索引堆更新了最后 1 个数,因此最后还要看一眼最大值
res.append(index_max_heap.peek_max_value())
return res
class IndexMaxHeap:
def __init__(self, capacity):
self.data = [None for _ in range(capacity + 1)]
# 初值设置为 0 ,表示该位置还没有放置元素
self.indexes = [0 for _ in range(capacity + 1)]
self.reverse = [0 for _ in range(capacity + 1)]
self.count = 0
self.capacity = capacity
def size(self):
return self.count
def is_empty(self):
return self.count == 0
# 此时 insert 要给一个索引位置
def insert(self, i, item):
if self.count + 1 > self.capacity:
raise Exception('堆的容量不够了')
i += 1
self.data[i] = item
# 这一步很关键,在内部索引数组的最后设置索引数组的索引
self.indexes[self.count + 1] = i
self.reverse[i] = self.count + 1
self.count += 1
self.__shift_up(self.count)
def __shift_up(self, k):
while k > 1 and self.data[self.indexes[k // 2]] < self.data[self.indexes[k]]:
self.indexes[k // 2], self.indexes[k] = self.indexes[k], self.indexes[k // 2]
self.reverse[self.indexes[k // 2]] = k // 2
self.reverse[self.indexes[k]] = k
k //= 2
def extract_max(self):
if self.count == 0:
raise Exception('堆里没有可以取出的元素')
ret = self.data[self.indexes[1]]
self.indexes[1], self.indexes[self.count] = self.indexes[self.count], self.indexes[1]
self.reverse[self.indexes[1]] = 1
self.reverse[self.indexes[self.count]] = self.count
self.reverse[self.indexes[self.count]] = 0
self.count -= 1
self.__shift_down(1)
return ret
def __shift_down(self, k):
while 2 * k <= self.count:
j = 2 * k
if j + 1 <= self.count and self.data[self.indexes[j + 1]] > self.data[self.indexes[j]]:
j = j + 1
if self.data[self.indexes[k]] >= self.data[self.indexes[j]]:
break
self.indexes[k], self.indexes[j] = self.indexes[j], self.indexes[k]
self.reverse[self.indexes[k]] = k
self.reverse[self.indexes[j]] = j
k = j
# 新增方法
def extract_max_index(self):
assert self.count > 0
# 减 1 是为了符合用户视角
ret = self.indexes[1] - 1
self.indexes[1], self.indexes[self.count] = self.indexes[self.count], self.indexes[1]
self.count -= 1
self.__shift_down(1)
return ret
# 新增方法
def get_item(self, i):
# 内部数组的索引比用户视角多 1
return self.data[i + 1]
# 新增方法
def change(self, i, new_item):
# 把用户视角改成内部索引
i += 1
self.data[i] = new_item
# 重点:下面这一步是找原来数组中索引是 i 的元素
# 在索引数组中的索引是几,这是一个唯一值,找到即返回
# 优化:可以引入反向查找技术优化
j = self.reverse[i]
self.__shift_down(j)
self.__shift_up(j)
# 为 LeetCode 第 239 题新增的方法,看一眼此时索引堆的最大索引是多少(没用上,我想多了,留到以后用吧)
def peek_max_index(self):
if self.count == 0:
raise Exception('堆里没有可以取出的元素')
# 注意:与用户认为的索引值有一个偏差
return self.indexes[1] - 1
# 为 LeetCode 第 239 题新增的方法,看一眼此时索引堆的最大值是多少
def peek_max_value(self):
if self.count == 0:
raise Exception('堆里没有可以取出的元素')
return self.data[self.indexes[1]]
if __name__ == '__main__':
solution = Solution()
nums = [1, 3, -1, -3, 5, 3, 6, 7]
k = 3
res = solution.maxSlidingWindow(nums, k)
print(res)
Java 代码:
import java.util.Arrays;
/**
* @author liwei
* @date 2019/7/10 9:27 AM
*/
public class Solution2 {
public int[] maxSlidingWindow(int[] nums, int k) {
int len = nums.length;
if (len == 0) {
return new int[]{};
}
// 初始化最大索引堆,其容量是滑动窗口的大小
IndexMaxHeap indexMaxHeap = new IndexMaxHeap(k);
// 首先先把前 k 个元素加进去
for (int i = 0; i < k; i++) {
indexMaxHeap.insert(i, nums[i]);
}
// 结果集
int[] res = new int[len - k + 1];
// 然后就是产生滑动窗口的过程,先输出最大值,
// 而后把当前考虑的数插入到将要滑出的左边界的索引位置
for (int i = k; i < len; i++) {
res[i - k] = indexMaxHeap.peekMaxValue();
indexMaxHeap.change(i % k, nums[i]);
}
// 因为最大索引堆更新了最后 1 个数,因此最后还要看一眼最大值
res[len - k] = indexMaxHeap.peekMaxValue();
return res;
}
class IndexMaxHeap {
private int[] data;
private int count;
private int capacity;
private int[] indexes;
private int[] reverse;
// 使用了反向查找技术的最大索引堆
public IndexMaxHeap(int capacity) {
data = new int[capacity + 1];
indexes = new int[capacity + 1];
reverse = new int[capacity + 1];
count = 0;
this.capacity = capacity;
}
public int getSize() {
return count;
}
public boolean isEmpty() {
return count == 0;
}
public void insert(int i, int item) {
assert count + 1 <= capacity;
assert i + 1 >= 1 && i + 1 <= capacity;
i += 1;
data[i] = item;
indexes[count + 1] = i;
reverse[i] = indexes[count + 1];
count++;
shiftUp(count);
}
private void shiftUp(int k) {
while (k > 1 && data[indexes[k / 2]] < data[indexes[k]]) {
swap(indexes, k / 2, k);
// 注意分析这行代码,即使上一行 indexes 的两个元素交换了位置,但是并没有改变他们的值
// 每一次交换了 indexes 索引以后,还要把 reverse 索引也交换
swap(reverse, indexes[k / 2], indexes[k]);
k /= 2;
}
}
private void shiftUp1(int k) {
while (k > 1 && data[indexes[k / 2]] < data[indexes[k]]) {
swapIndexes(k / 2, k);
k /= 2;
}
}
private void swapIndexes(int index1, int index2) {
if (index1 == index2) {
return;
}
int temp = indexes[index1];
indexes[index1] = indexes[index2];
indexes[index2] = temp;
reverse[indexes[index1]] = index2;
reverse[indexes[index2]] = index1;
}
private void swap(int[] data, int index1, int index2) {
if (index1 == index2) {
return;
}
int temp = data[index1];
data[index1] = data[index2];
data[index2] = temp;
}
/**
* @return
*/
public int extractMax() {
// 将此时二叉堆中的最大的那个数据删除(出队),返回的是数据,不是返回索引
assert count > 0;
int ret = data[indexes[1]];
// 只要设计交换的操作,就一定是索引数组交换
// 每一次交换了 indexes 索引以后,还要把 reverse 索引也交换
swap(indexes, 1, count);
swap(reverse, indexes[1], indexes[count]);
count--;
shiftDown(1);
return ret;
}
/**
* @return
*/
public int extractMax1() {
// 将此时二叉堆中的最大的那个数据删除(出队),返回的是数据,不是返回索引
assert count > 0;
int ret = data[indexes[1]];
// 只要设计交换的操作,就一定是索引数组交换
// 每一次交换了 indexes 索引以后,还要把 reverse 索引也交换
swapIndexes(1, count);
count--;
shiftDown(1);
return ret;
}
private void shiftDown(int k) {
while (2 * k <= count) {
int j = 2 * k;
if (j + 1 <= count && data[indexes[j + 1]] > data[indexes[j]]) {
j = j + 1;
}
if (data[indexes[k]] >= data[indexes[j]]) {
break;
}
// 每一次交换了 indexes 索引以后,还要把 reverse 索引也交换
swap(indexes, k, j);
swap(reverse, indexes[k], indexes[j]);
k = j;
}
}
private void shiftDown1(int k) {
while (2 * k <= count) {
int j = 2 * k;
if (j + 1 <= count && data[indexes[j + 1]] > data[indexes[j]]) {
j = j + 1;
}
if (data[indexes[k]] >= data[indexes[j]]) {
break;
}
// 每一次交换了 indexes 索引以后,还要把 reverse 索引也交换
swapIndexes(k, j);
k = j;
}
}
public int extractMaxIndex() {
assert count > 0;
int ret = indexes[1] - 1;
// 每一次交换了 indexes 索引以后,还要把 reverse 索引也交换
swap(indexes, 1, count);
swap(reverse, indexes[1], indexes[count]);
count--;
shiftDown(1);
return ret;
}
public int extractMaxIndex1() {
assert count > 0;
int ret = indexes[1] - 1;
// 每一次交换了 indexes 索引以后,还要把 reverse 索引也交换
swapIndexes(1, count);
count--;
shiftDown(1);
return ret;
}
public int getItem(int i) {
return data[i + 1];
}
public void change(int i, int item) {
i = i + 1;
data[i] = item;
// 原先遍历的操作,现在就变成了这一步,是不是很酷
int j = reverse[i];
shiftDown(j);
shiftUp(j);
}
/**
* 为 LeetCode 第 239 题新增的方法,
* 看一眼此时索引堆的最大索引是多少(没用上,我想多了,留到以后用吧)
*
* @return
*/
public int peekMaxIndex() {
if (this.count == 0) {
throw new RuntimeException("堆里没有可以取出的元素");
}
// 注意:与用户认为的索引值有一个偏差
return indexes[1] - 1;
}
/**
* 为 LeetCode 第 239 题新增的方法,
* 看一眼此时索引堆的最大索引是多少(没用上,我想多了,留到以后用吧)
*
* @return
*/
public int peekMaxValue() {
if (this.count == 0) {
throw new RuntimeException("堆里没有可以取出的元素");
}
return data[indexes[1]];
}
}
public static void main(String[] args) {
Solution2 solution2 = new Solution2();
int[] nums = {1, 3, -1, -3, 5, 3, 6, 7};
int k = 3;
int[] res = solution2.maxSlidingWindow(nums, k);
System.out.println(Arrays.toString(res));
}
}