LeetCode 第 106 题:“从中序与后序遍历序列构造二叉树”题解
题解地址:分治法(Python、Java)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:106. 从中序与后序遍历序列构造二叉树。
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树:
3/
9 20 /
15 7
分治法(Python、Java)
思路分析:
二叉树相关的很多问题的解决思路都有分治法的思想在里面。
复习一下分治法的思想:把原问题拆解成若干个与原问题结构相同但规模更小的子问题,待子问题解决以后,原问题就得以解决,“归并排序” 和 “快速排序” 都是分治法思想的应用,其中 “归并排序” 先无脑地“分”,在 “合” 的时候就麻烦一些;“快速排序” 开始在 partition 上花了很多时间,即在 “分” 上使了很多劲,然后就递归处理下去就好了,没有在 “合” 上再花时间。
以题目中给出的例子为例,讲解如何构建二叉树。
中序遍历
inorder = [9,3,15,20,7]
后序遍历postorder = [9,15,7,20,3]
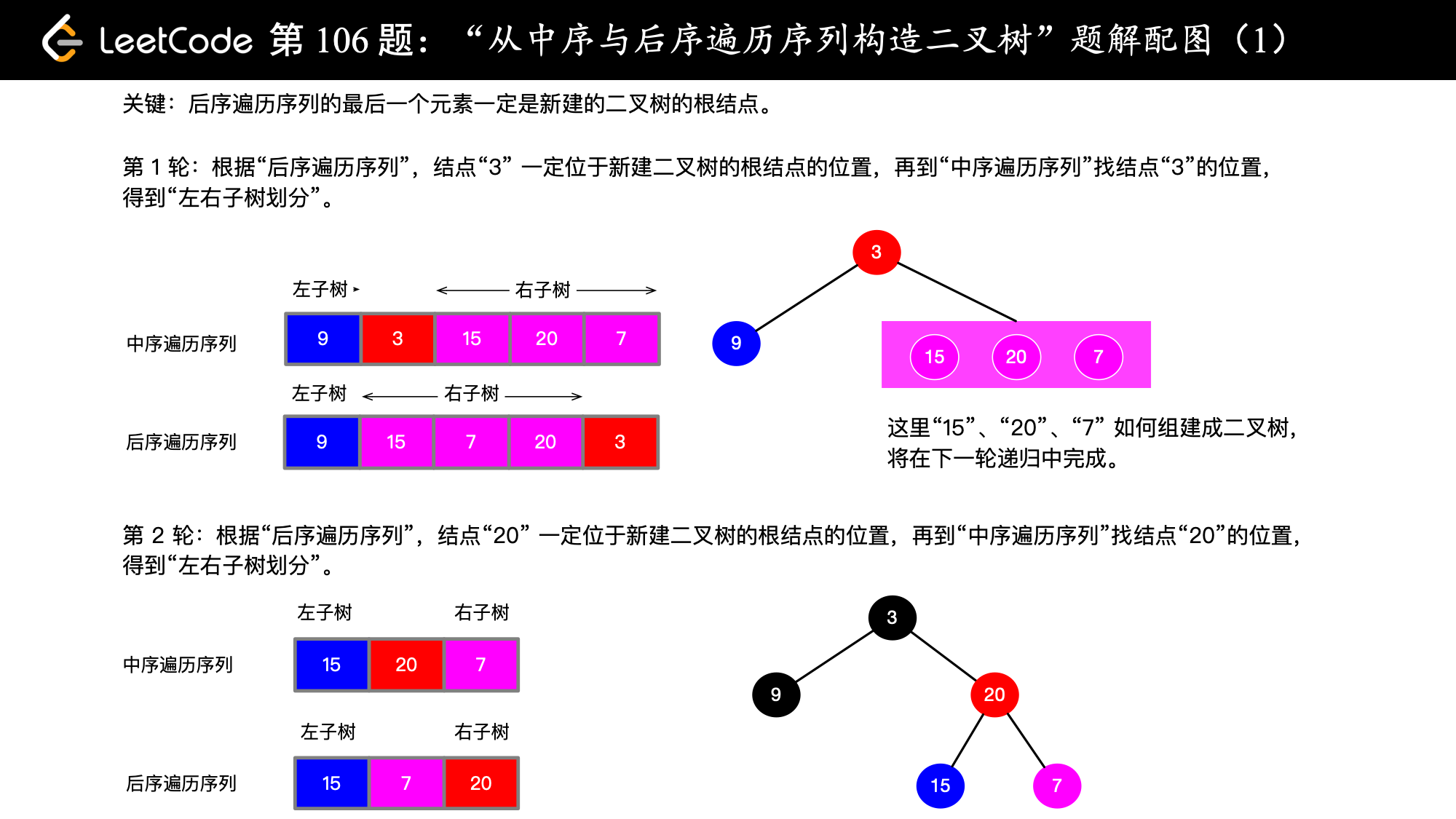
图画完以后才发现这个例子不太好,数组长度多一些就能把思路展现得更清楚了,各位客官老爷将就看一下啦。或者可以看一下我写的「力扣」第 105 题的题解《分治法(Python 代码、Java 代码)》,两道问题的解法是一样的。
注意:这道问题其实并不难,我们在草稿纸上写写画画,就能把思路想清楚,但是在编码上会有一些小陷阱,在计算索引边界值要认真一些。
下面给出两种写法,区别在于空间复杂度:
方法一:在递归方法中,传入数组的拷贝(了解,不推荐)
该方法在计算索引的时候会稍微容易一些。
参考代码 1:
Python 代码:
from typing import List
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
assert len(inorder) == len(postorder)
if len(inorder) == 0:
return None
if len(inorder) == 1:
# 这里要返回结点,而不是返回具体的数
return TreeNode(inorder[0])
# 后序遍历的最后一个结点就是根结点
root = TreeNode(postorder[-1])
# 在中序遍历中找到根结点的索引,得到左右子树的一个划分
pos = inorder.index(postorder[-1])
# 这里的列表切片使用的是复制值,使用了一些空间,因此空间复杂度是 O(N)
root.left = self.buildTree(inorder[:pos], postorder[:pos])
root.right = self.buildTree(inorder[pos + 1:], postorder[pos:-1])
return root
Java 代码:
import java.util.Arrays;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution {
/**
* @param inorder 中序遍历序列
* @param postorder 后序遍历序列
* @return
*/
public TreeNode buildTree(int[] inorder, int[] postorder) {
int inlen = inorder.length;
int postlen = postorder.length;
assert inlen == postlen;
if (inlen == 0) {
return null;
}
if (inlen == 1) {
return new TreeNode(inorder[0]);
}
// 后序遍历的最后一个结点就是根结点
int rootVal = postorder[postlen - 1];
// 在中序遍历中找到根结点的索引,得到左右子树的一个划分
int dividePoint = 0;
for (int i = 0; i < inlen; i++) {
if (inorder[i] == rootVal) {
dividePoint = i;
break;
}
}
TreeNode rootNode = new TreeNode(rootVal);
// Arrays.copyOfRange() 方法的第 1 个参数是源数组
// 第 2 个参数是源数组的起始位置(可以取到)
// 第 3 个参数是源数组的起始位置(不可以取到)
// 这里复制了数组,使用了一些空间,因此空间复杂度是 O(N)
rootNode.left = buildTree(Arrays.copyOfRange(inorder, 0, dividePoint), Arrays.copyOfRange(postorder, 0, dividePoint));
rootNode.right = buildTree(Arrays.copyOfRange(inorder, dividePoint + 1, inlen), Arrays.copyOfRange(postorder, dividePoint, postlen - 1));
return rootNode;
}
}
复杂度分析:
- 时间复杂度:,这里 是二叉树的结点个数,算法中每个结点都会被看到一次,是线性级别的,递归的深度是对数级别的,因此时间复杂度是 。
- 空间复杂度:,构造一棵树需要 个结点(待讨论)。
方法二:在递归方法中,传入子数组的边界索引
注意:在递归方法中,有一个数组的边界索引,得通过计算得到,计算的依据是递归方法传入的“中序遍历数组”(的子数组)和“后序遍历数组”(的子数组)的长度是一样的。我的办法是解方程计算未知数,哈哈,傻呼呼的。具体需要计算哪个参数我在下面的代码中已经注明了。
参考代码 2:
Python 代码:
from typing import List
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def __init__(self):
self.inorder = None
self.postorder = None
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
assert len(inorder) == len(postorder)
size = len(inorder)
self.inorder = inorder
self.postorder = postorder
return self.__dfs(0, size - 1, 0, size - 1)
def __dfs(self, in_l, in_r, post_l, post_r):
if in_l > in_r or post_l > post_r:
return None
val = self.postorder[post_r]
# 后序遍历的最后一个结点就是根结点
root = TreeNode(val)
# 在中序遍历中找到根结点的索引,得到左右子树的一个划分
pos = self.inorder.index(val)
# 注意:第 4 个参数是计算出来的,依据:两边区间长度相等
root.left = self.__dfs(in_l, pos - 1, post_l, pos - 1 - in_l + post_l)
# 注意:第 3 个参数是计算出来的,依据:两边区间长度相等
root.right = self.__dfs(pos + 1, in_r, post_r - in_r + pos, post_r - 1)
return root
Java 代码:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution {
private int[] inorder;
private int[] postorder;
public TreeNode buildTree(int[] inorder, int[] postorder) {
this.inorder = inorder;
this.postorder = postorder;
int len = inorder.length;
return dfs(0, len - 1, 0, len - 1);
}
private TreeNode dfs(int inl, int inr, int postl, int postr) {
if (inl > inr || postl > postr) {
return null;
}
int val = postorder[postr];
int k = 0;
for (int i = inl; i < inr + 1; i++) {
if (inorder[i] == val) {
k = i;
break;
}
}
TreeNode root = new TreeNode(val);
// 注意:第 4 个参数是计算出来的,依据:两边区间长度相等
root.left = dfs(inl, k - 1, postl, k - 1 - inl + postl);
// 注意:第 3 个参数是计算出来的,依据:两边区间长度相等
root.right = dfs(k + 1, inr, postr + k - inr, postr - 1);
return root;
}
public static void main(String[] args) {
int[] inorder = {1, 3, 2};
int[] postorder = {3, 2, 1};
Solution solution = new Solution();
TreeNode res = solution.buildTree(inorder, postorder);
System.out.println(res);
}
}
复杂度分析:
- 时间复杂度:,这里 是二叉树的结点个数,算法中每个结点都会被看到一次,是线性级别的,递归的深度是对数级别的,因此时间复杂度是 。
- 空间复杂度:,构造一棵树需要 个结点(待讨论)。