LeetCode 第 105 题：“从前序与中序遍历序列构造二叉树”题解

说明：文本首发在力扣的题解版块，更新也会在第 1 时间在上面的网站中更新，这篇文章只是上面的文章的一个快照，您可以点击上面的链接看到其他网友对本文的评论。

根据一棵树的前序遍历与中序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树：

3 /
9 20 /
15 7

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

分治法（Python 代码、Java 代码）

思路分析：

二叉树相关的很多问题的解决思路都有分治法的思想在里面。我们复习一下分治法的思想：把原问题拆解成若干个与原问题结构相同但规模更小的子问题，待子问题解决以后，原问题就得以解决，“归并排序”和“快速排序”都是分治法思想的应用，其中“归并排序”先无脑地“分”，在“合”的时候就麻烦一些；“快速排序”开始在 partition 上花了很多时间，即在“分”上使了很多劲，然后就递归处理下去就好了，没有在“合”上再花时间。

抓住“前序遍历的第 1 个元素一定是二叉树的根结点”，不难写出代码。关键还是拿 LeetCode 上面的例子画一个图，思路就很清晰了。

前序遍历数组的第 $1$ 个数（索引为 $0$ ）的数一定是二叉树的根结点，于是可以在中序遍历中找这个根结点的索引，然后把“前序遍历数组”和“中序遍历数组”分为两个部分，就分别对应二叉树的左子树和右子树，分别递归完成就可以了。

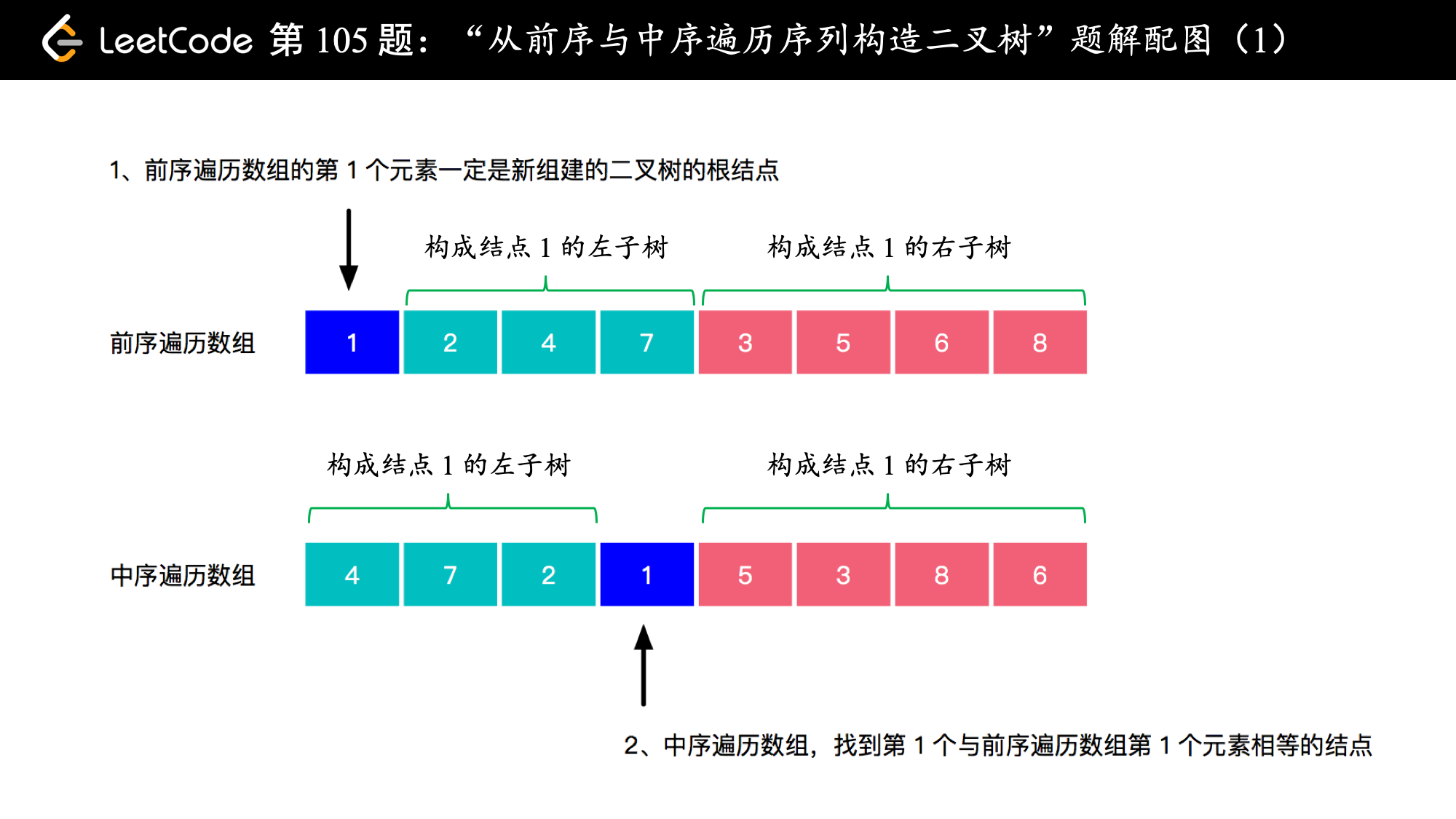
这道题完成了以后可以顺便把「力扣」第 106 题：从中序与后序遍历序列构造二叉树也一起做了，加油加油！

参考代码：

Python 代码：

class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None


class Solution(object):

    def buildTree(self, preorder, inorder):
        plen = len(preorder)
        ilen = len(inorder)
        return self.__helper(preorder, 0, plen - 1, inorder, 0, ilen - 1)

    def __helper(self, preorder, prel, prer,
                 inorder, inl, inr):
        if prel > prer:
            return None
        root_val = preorder[prel]
        l = inl
        while l < inr and inorder[l] != root_val:
            l += 1
        # 走到这里 inorder[l] == root 为 True
        root_node = TreeNode(root_val)
        root_node.left = self.__helper(preorder, prel + 1, prel + l - inl,
                                       inorder, inl, l - 1)
        root_node.right = self.__helper(preorder, prel + l - inl + 1, prer,
                                        inorder, l + 1, inr)
        return root_node

Java 代码：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

public class Solution {

    // 使用前序遍历和中序遍历构建二叉树
    // 举出具体例子来分析就会很清晰，这里一定要分析清楚索引的起始
    // 例如：
    // pre: A B D E H I C F K G
    // in : D B H E I A F K C G

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int preLen = preorder.length;
        int inLen = inorder.length;
        return helper(preorder, 0, preLen - 1, inorder, 0, inLen - 1);
    }


    private TreeNode helper(int[] preorder,
                            int preL, int preR,
                            int[] inorder,
                            int inL, int inR) {
        if (preL > preR || inL > inR) {
            return null;
        }
        int rootVal = preorder[preL];
        int l = inL;
        while (l <= inR && inorder[l] != rootVal) {
            l++;
        }
        TreeNode root = new TreeNode(rootVal);
        root.left = helper(preorder, preL + 1, preL + l - inL, inorder, inL, l - 1);
        root.right = helper(preorder, preL + l - inL + 1, preR, inorder, l + 1, inR);
        return root;
    }
}

复杂度分析：

时间复杂度： $O(N)$ ，这里 $N$ 是二叉树的结点个数。
空间复杂度： $O(N)$ 。

LeetCode 第 106 题：“从中序与后序遍历序列构造二叉树”题解 →

# LeetCode 第 105 题：“从前序与中序遍历序列构造二叉树”题解

# 分治法（Python 代码、Java 代码）

LeetCode 第 105 题：“从前序与中序遍历序列构造二叉树”题解

分治法（Python 代码、Java 代码）