LeetCode 第 421 题:“数组中两个数的最大异或值”题解
题解地址:利用异或运算的性质 + 贪心算法(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:421. 数组中两个数的最大异或值。
给定一个非空数组,数组中元素为 a0, a1, a2, … , an-1,其中 0 ≤ ai < 231 。
找到 ai 和aj 最大的异或 (XOR) 运算结果,其中0 ≤ i, j < n 。
你能在O(n)的时间解决这个问题吗?
示例:
输入: [3, 10, 5, 25, 2, 8]
输出: 28
解释: 最大的结果是 5 ^ 25 = 28.
利用异或运算的性质 + 贪心算法(Python 代码、Java 代码)
异或运算的性质
解决这个问题,我们首先需要利用异或运算的一个性质:
如果
a ^ b = c成立,那么a ^ c = b与b ^ c = a均成立。
即 如果有三个数,满足其中两个数的异或值等于另一个值,那么这三个数的顺序可以任意调换。
(说明:利用这条性质,可以不使用第 3 个变量而交换两个变量的值。)
- 那么如何理解这个性质呢?因为异或运算其实就是 二进制下不进位的加法,你不妨自己举几个例子,在草稿纸上验证一下。
如何应用到本题?
这道题找最大值的思路是这样的:因为两两异或可以得到一个值,在所有的两两异或得到的值中,一定有一个最大值,我们推测这个最大值应该是什么样的?即根据“最大值”的存在性解题(一定存在)。在这里要强调一下:
我们只用关心这个最大的异或值需要满足什么性质,进而推出这个最大值是什么,而不必关心这个异或值是由哪两个数得来的。
(上面这句话很重要,如果读者一开始看不明白下面的思考,不妨多看几遍我上面写的这句话。)
于是有如下思考:
1、二进制下,我们希望一个数尽可能大,即希望越高位上越能够出现“1”,这样这个数就是所求的最大数,这是贪心算法的思想。
2、于是,我们可以从最高位开始,到最低位,首先假设高位是 “1”,把这 n 个数全部遍历一遍,看看这一位是不是真的可以是“1”,否则这一位就得是“0”,判断的依据是上面“异或运算的性质”,即下面的第 3 点;
3、如果 a ^ b = max 成立 ,max 表示当前得到的“最大值”,那么一定有 max ^ b = a 成立。我们可以先假设当前数位上的值为 “1”,再把当前得到的数与这个 n 个数的 前缀(因为是从高位到低位看,所以称为“前缀”)进行异或运算,放在一个哈希表中,再依次把所有 前缀 与这个假设的“最大值”进行异或以后得到的结果放到哈希表里查询一下,如果查得到,就说明这个数位上可以是“1”,否则就只能是 0(看起来很晕,可以看代码理解)。
一种极端的情况是,这 n 个数在某一个数位上全部是 0 ,那么任意两个数异或以后都只能是 0,那么假设当前数位是 1 这件事情就不成立。
4、如何得到前缀,可以用掩码(mask),掩码可以进行如下构造,将掩码与原数依次进行 “与” 运算,就能得到前缀。
10000000000000000000000000000000
11000000000000000000000000000000
11100000000000000000000000000000
11110000000000000000000000000000
11111000000000000000000000000000
11111100000000000000000000000000
11111110000000000000000000000000
11111111000000000000000000000000
11111111100000000000000000000000
11111111110000000000000000000000
11111111111000000000000000000000
11111111111100000000000000000000
11111111111110000000000000000000
11111111111111000000000000000000
11111111111111100000000000000000
11111111111111110000000000000000
11111111111111111000000000000000
11111111111111111100000000000000
11111111111111111110000000000000
11111111111111111111000000000000
11111111111111111111100000000000
11111111111111111111110000000000
11111111111111111111111000000000
11111111111111111111111100000000
11111111111111111111111110000000
11111111111111111111111111000000
11111111111111111111111111100000
11111111111111111111111111110000
11111111111111111111111111111000
11111111111111111111111111111100
11111111111111111111111111111110
11111111111111111111111111111111
以题目中的数组 [3, 10, 5, 25, 2, 8] 为例,下面讲解这个最大的两两异或值是如何得到的,这里为了方便演示,只展示一个数二进制的低 8 位。
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
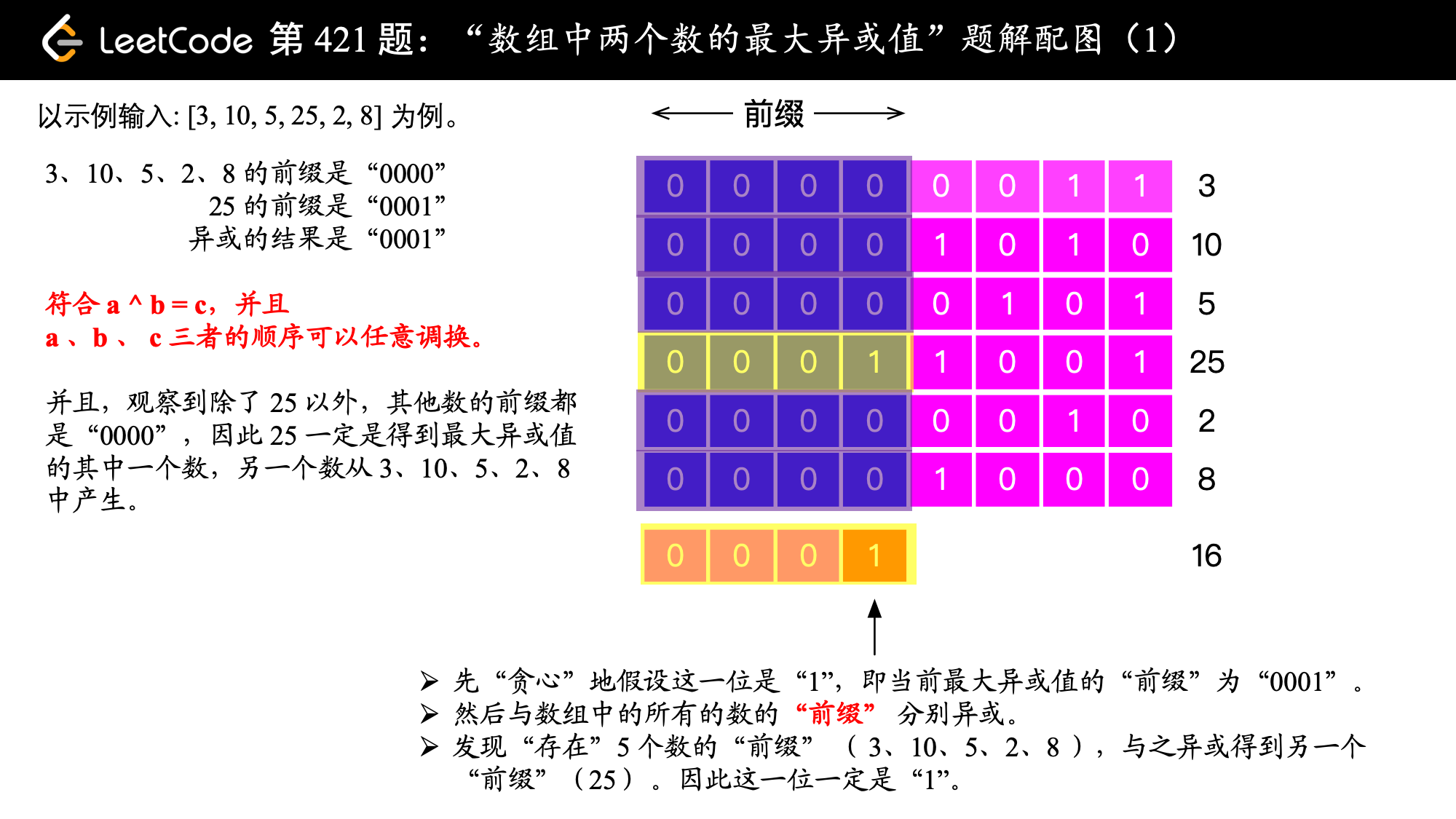 ,
,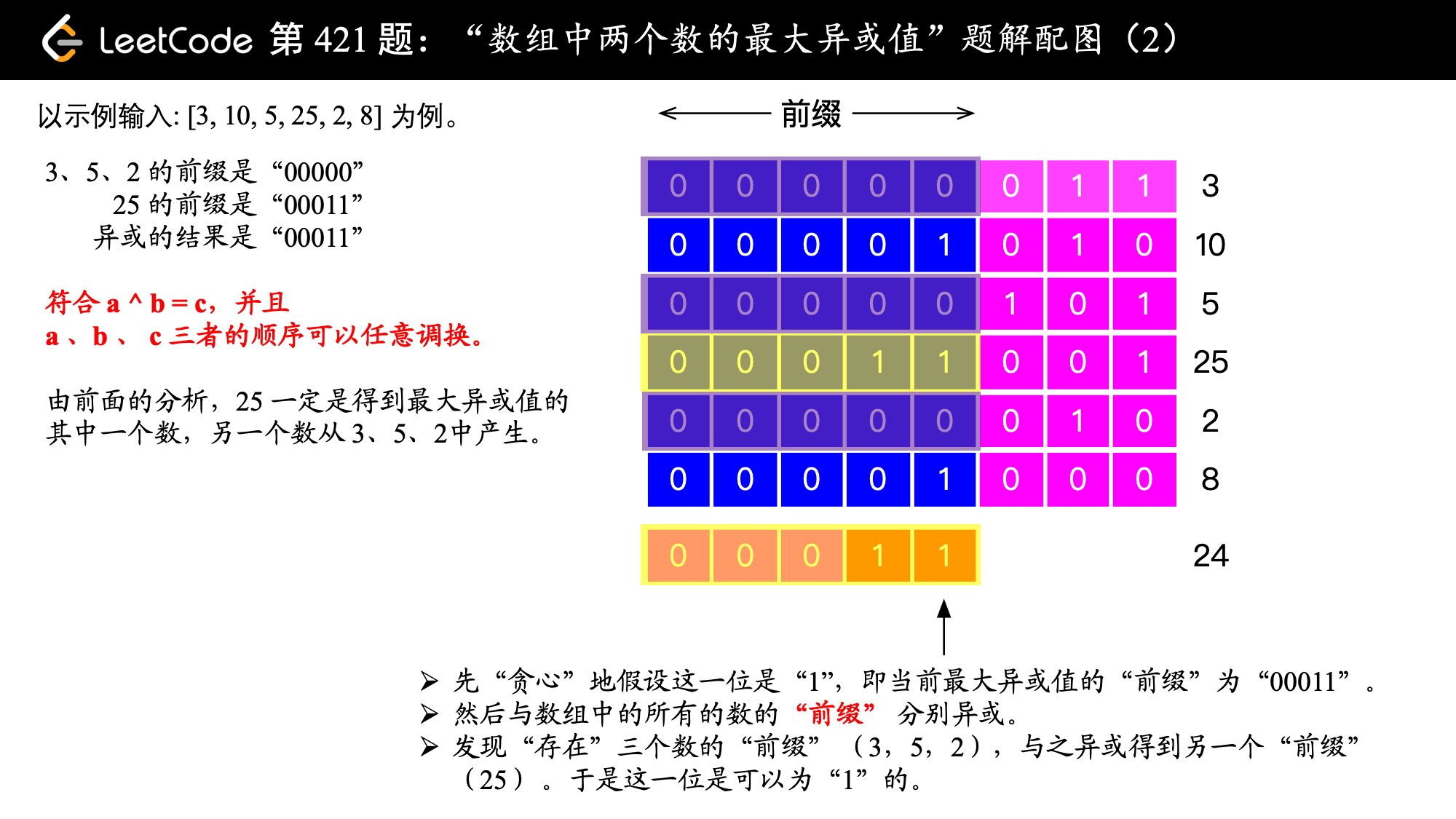 ,
,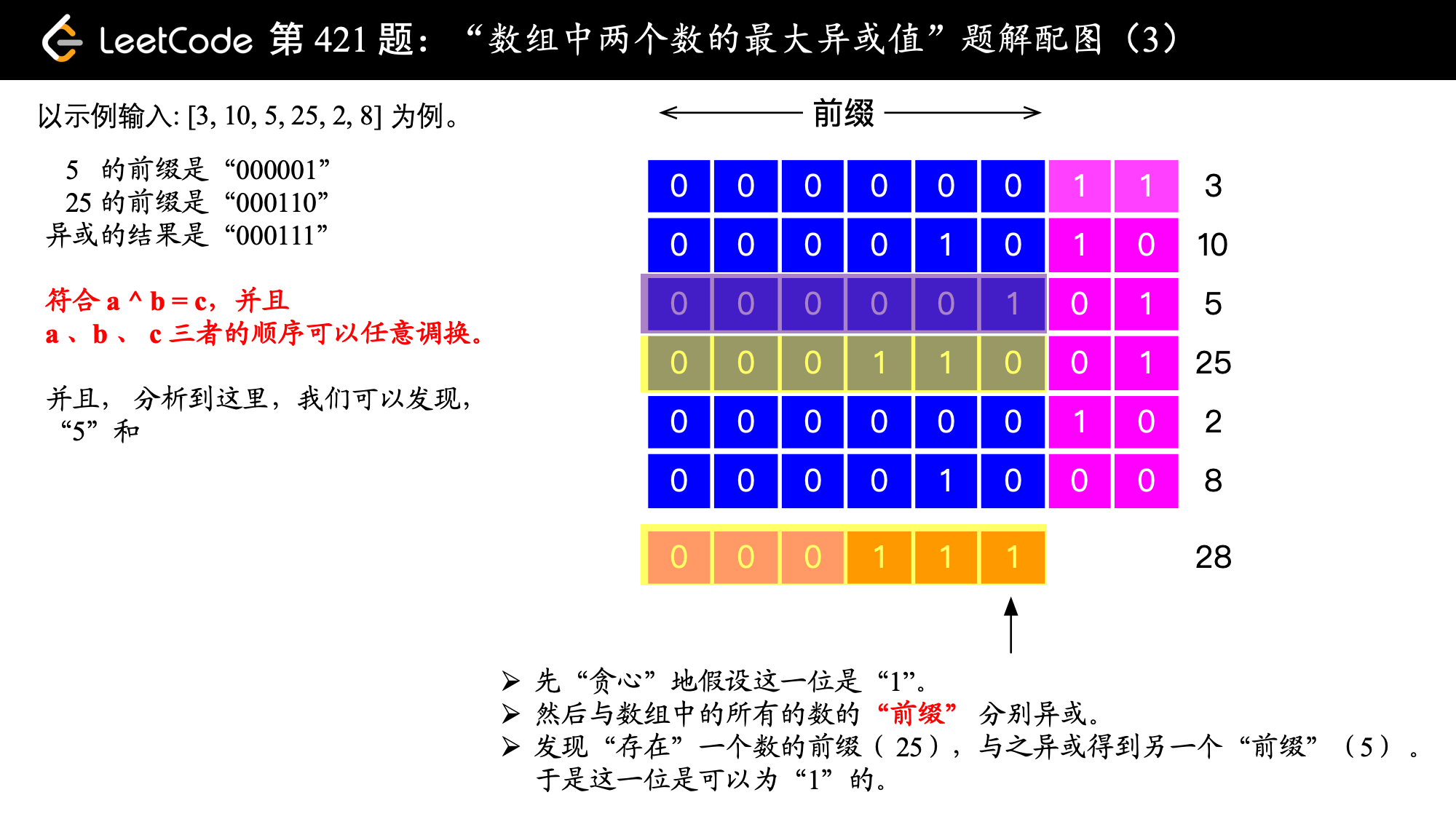 ,
,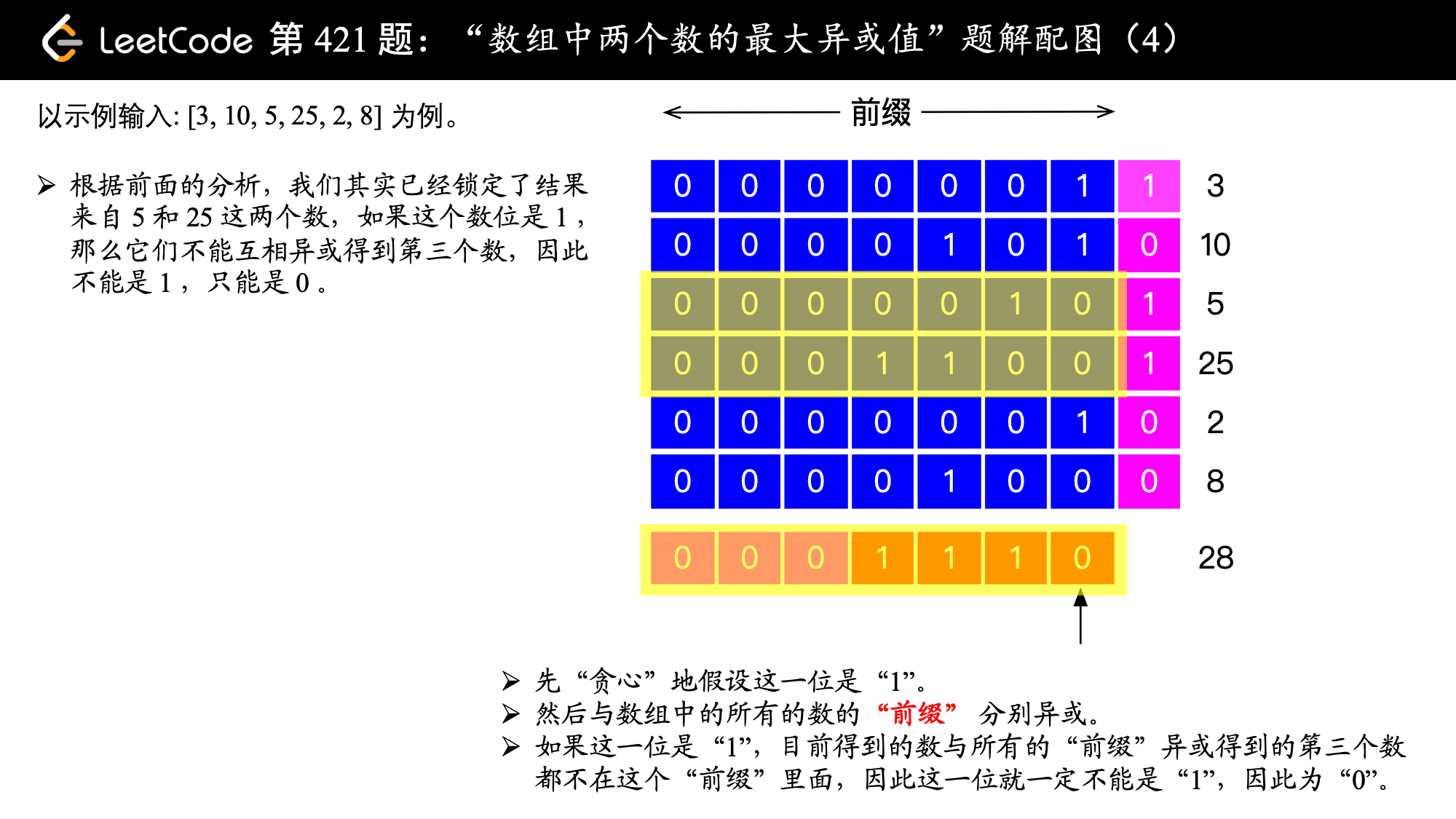 ,
,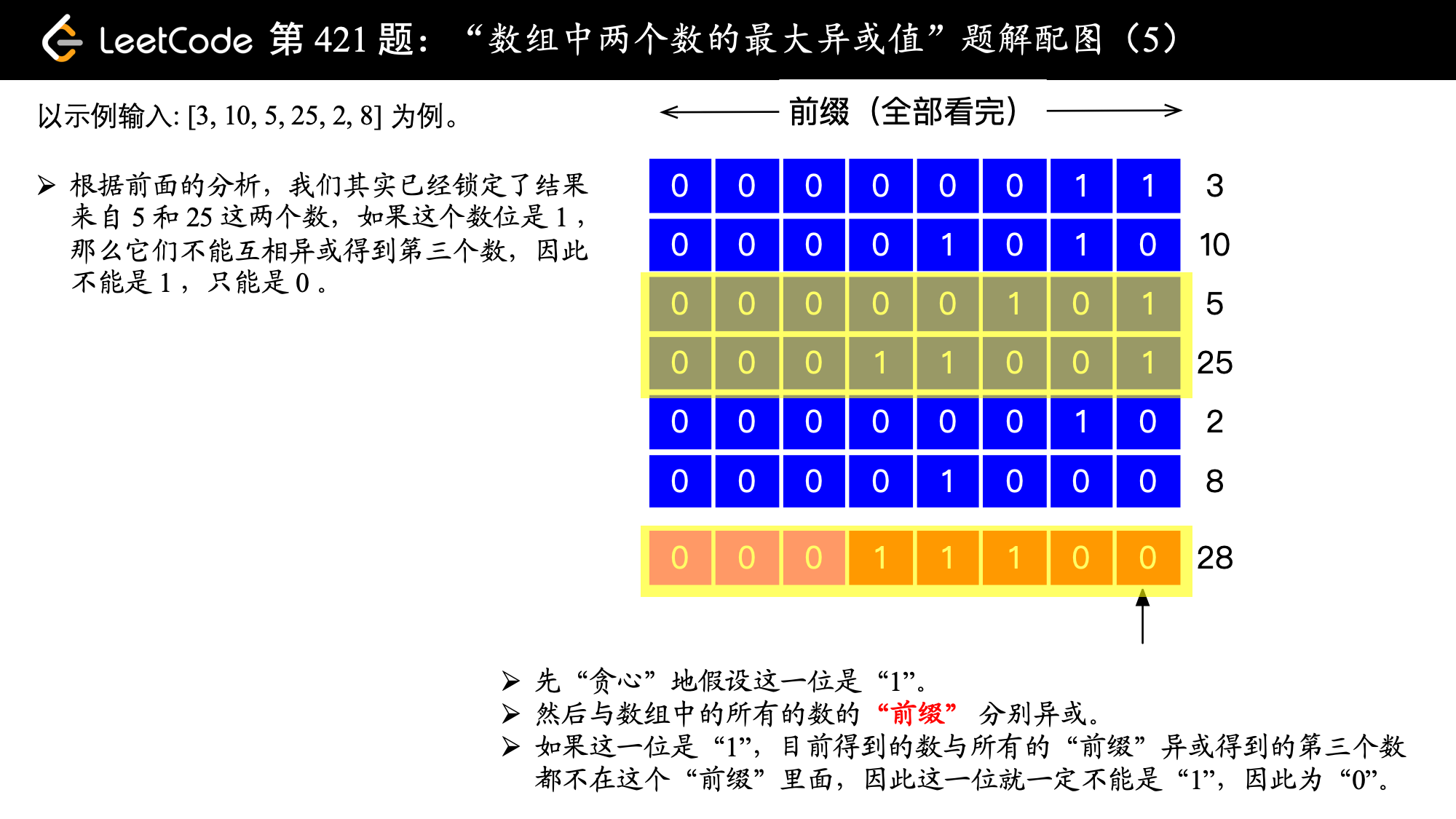 ,
,
参考代码:
Python 代码:
class Solution:
def findMaximumXOR(self, nums: List[int]) -> int:
res = 0
mask = 0
for i in range(31, -1, -1):
mask |= (1 << i)
# 当前得到的所有前缀都放在这个哈希表中
s = set()
for num in nums:
s.add(mask & num)
# 先“贪心地”假设这个数位上是 “1” ,如果全部前缀都看完,都不符合条件,这个数位上就是 “0”
temp = res | (1 << i)
for prefix in s:
if temp ^ prefix in s:
res = temp
break
return res
Java 代码:
import java.util.HashSet;
import java.util.Set;
public class Solution {
// 先确定高位,再确定低位(有点贪心算法的意思),才能保证这道题的最大性质
// 一位接着一位去确定这个数位的大小
// 利用性质: a ^ b = c ,则 a ^ c = b,且 b ^ c = a
public int findMaximumXOR(int[] nums) {
int res = 0;
int mask = 0;
for (int i = 31; i >= 0; i--) {
// 注意点1:注意保留前缀的方法,mask 是这样得来的
// 用异或也是可以的 mask = mask ^ (1 << i);
mask = mask | (1 << i);
// System.out.println(Integer.toBinaryString(mask));
Set<Integer> set = new HashSet<>();
for (int num : nums) {
// 注意点2:这里使用 & ,保留前缀的意思(从高位到低位)
set.add(num & mask);
}
// 这里先假定第 n 位为 1 ,前 n-1 位 res 为之前迭代求得
int temp = res | (1 << i);
for (Integer prefix : set) {
if (set.contains(prefix ^ temp)) {
res = temp;
break;
}
}
}
return res;
}
public static void main(String[] args) {
int[] nums = {3, 10, 5, 25, 2, 8};
Solution solution = new Solution();
int maximumXOR = solution2.findMaximumXOR(nums);
System.out.println(maximumXOR);
}
}
复杂度分析:
- 时间复杂度:,把整个数组看了 次,即 。
- 空间复杂度:,这里的 是哈希表的长度,具体长度是多少,与输入的规模、扩容策略、负载因子和冲突策略等有关。例如 Java 在 JDK 1.8 以后,当哈希值冲突的时候,先把冲突的元素放在单链表上,当冲突的键值大于 8 的时候,再转成红黑树。 参考资料:《jdk8中HashMap的优化和底层内存的优化》。