LeetCode 第 611 题:“有效三角形的个数”题解
题解地址:二分查找 (Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:611. 有效三角形的个数。
给定一个包含非负整数的数组,你的任务是统计其中可以组成三角形三条边的三元组个数。
示例 1:
输入: [2,2,3,4] 输出: 3 解释: 有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3 注意:
数组长度不超过1000。 数组里整数的范围为 [0, 1000]。
二分查找 (Python 代码、Java 代码)
思路分析:
这道题是朋友邀请我做的,我的第一感觉是:“先排序,然后根据两边之和大于第三边,两边之差小于第三边来做”,当然我也参考了评论区和题解区的代码,下面是我的思考过程。
一、考虑三条边能够组成三角形的充分必要条件
首先我们解决三条边构成三角形这件事情,我们脑子里会浮现出这样一句话:
三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边。
这是中学的数学知识告诉我们的,烦就烦在“任意”,三条边的任意组合我们都要看过去吗?不是的。
先看前半句话,“三角形的任意两边之和大于第三边”,事实上,只要最短的两条边大于第三边就好,剩下的就不用判断了,我的理由如下:既然边长是实数,不妨将这些边排个序。
假设有索引 i < j < k 使得 nums[i] <= nums[j] <= nums[k] 成立,不妨称它们为“短”、“中”、“长”,显然有:
- 在任何情况下,“短 + 长 > 中”成立。
- 在任何情况下,“中 + 长 > 短”成立。
再加上如果 nums[i] + nums[j] > nums[k] 成立,即“短 + 中 > 长”成立,那么“任意两边之和大于第三边”就一定成立。
另一方面,如果 nums[i] + nums[j] > nums[k] 成立,即“短 + 中 > 长”成立,它等价于:
- “长 - 短 < 中”成立;
- “长 - 中 < 短”成立;
而在任何情况下,“中 - 短 < 长”都成立,因此“三角形的任意两边之差小于第三边”也成立。
根据以上分析,我们得到:三条边能够成三角形的充分必要条件是:
较短的两边之和大于(不包括等于)第三边(最长边)。
二、思考如何编码?
不知道你会不会想起「力扣」第 15 题:三数之和,可以借鉴解这道题的“双指针”的办法来完成,但是是在有序数组中做,我们看一看二分查找有没有用武之地,写好一个二分查找不在话下,于是有以下两个方向。
1、先固定 i,然后固定 j,在剩下的区间里,找第 1 个不满足构成三角形的第三条边的索引:
(1)因为以后的边越来越长,这条边以及以后的边都不能和前面的两条边构成三角形;
(2)因为是第 1 个不满足构成三角形的第三条边,那这个索引和 j 之间的所有数都满足构成三角形,得到“一票解”(一系列解的意思),注意边界条件(边界条件一般在草稿纸上举例就很清楚了);
“找第 1 个不满足构成三角形的第三条边的索引”,在有序数组中,我们当然使用二分法,如图所示。
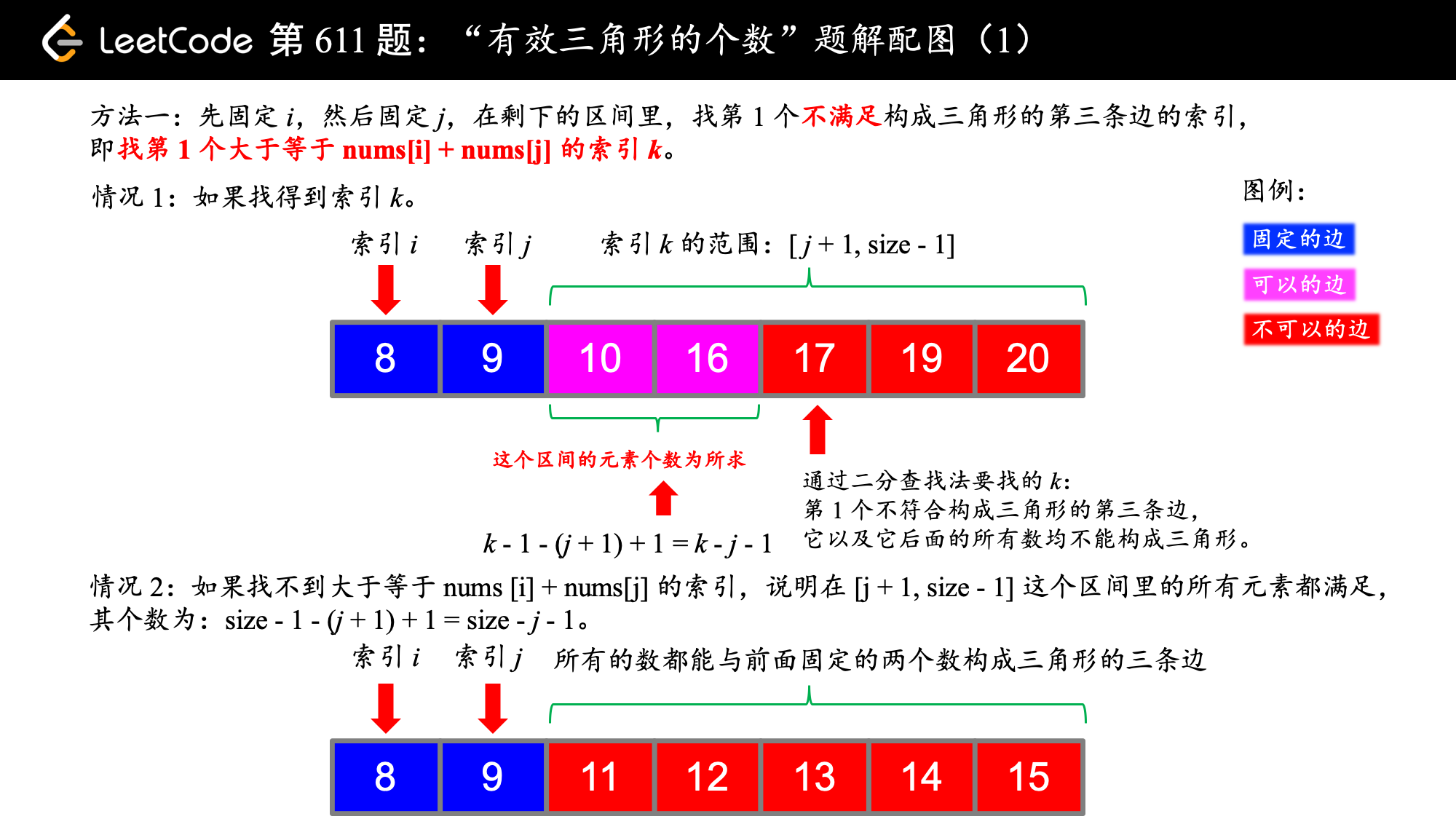
2、先固定 k,然后固定 j,在之前的区间里,找第 1 个满足构成三角形的第一条边的索引:
(1)因为之前的边是越来越短的,这条边之前边都不能和索引为 j 和 k 的两条边构成三角形;
(2)因为以后的边越来越长,这条边和 j 之间的所有数都满足构成三角形,得到“一票解”(一系列解的意思),注意边界条件(边界条件一般在草稿纸上举例就很清楚了)。
“找第 1 个满足构成三角形的第一条边的索引”,在有序数组中,我们当然还使用二分法,如图所示。

之所以我上面说“写好一个二分查找不在话下”,那是因为我做了很多“二分查找”的问题,我专门把我使用得最多的二分查找法模板,它好用的地方、使用它的技巧和注意事项整理在了「力扣」第 35 题:搜索插入位置的题解《特别好用的二分查找法模板(Python 代码、Java 代码)》,希望能对大家有所帮助。
方法:二分查找
参考代码 1: 先固定 i,再固定 j,然后找 k 的上界。
编码的时候写的草稿如下:

Python 代码:
from typing import List
class Solution:
def triangleNumber(self, nums: List[int]) -> int:
# 索引数组:[0, 1, 2, 3, 4],size = 5
# i 最多到倒数第 2 个索引
size = len(nums)
# 思路 1:从前到后,先固定 i ,再固定 j ,最后确定 k 的范围
# 首先不要忘记排序
nums.sort()
res = 0
# 注意边界,看上面那个索引数组知道 i 最多取到 2
for i in range(size - 2):
# 要给 k 留一个位置,故 size - 1 是上限(取不到)
for j in range(i + 1, size - 1):
# 在区间 [j + 1, size - 1] 中找第 1 个不能构成三角形的数
# k 与 j 之间的数的个数就是一票解
# 等价于,在子区间 [j + 1, size - 1] 里找第 1 个大于等于 nums[i] + nums[j] 的数
k = self.__find_first_cannot_triangle(nums, j + 1, size - 1, nums[i] + nums[j])
if k == -1:
# 说明子区间 [j + 1, size - 1] 全部的数都可以构成三角形
# 其中的数的个数为 size - 1 - (j + 1) + 1
res += (size - j - 1)
else:
# 说明子区间 [j + 1, k) 全部的数可以构成三角形,注意:这里 k 取不到
# 其中的数的个数为 k - (j + 1)
res += (k - j - 1)
return res
def __find_first_cannot_triangle(self, nums, left, right, target):
# 在 nums 的子区间 [left, right] 里找第 1 个大于等于 target 的元素的索引
# 如果不存在,返回 -1
while left < right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
else:
right = mid
# 后处理,因为很有可能找不到大于等于 target 的元素
if nums[left] < target:
return -1
return left
Java 代码:
import java.util.Arrays;
public class Solution {
public int triangleNumber(int[] nums) {
// 索引数组:[0, 1, 2, 3, 4],size = 5
// i 最多到倒数第 2 个索引
int len = nums.length;
// 思路 1:从前到后,先固定 i ,再固定 j ,最后确定 k 的范围
// 首先不要忘记排序
Arrays.sort(nums);
int res = 0;
// 注意边界,看上面那个索引数组知道 i 最多取到 2
for (int i = 0; i < len - 2; i++) {
// 要给 k 留一个位置,故 size - 1 是上限(取不到)
for (int j = i + 1; j < len - 1; j++) {
// 在区间 [j + 1, size - 1] 中找第 1 个不能构成三角形的数
// k 与 j 之间的数的个数就是一票解
// 等价于,在子区间 [j + 1, size - 1] 里找第 1 个大于等于 nums[i] + nums[j] 的数
int k = findFirstCanNotTriangle(nums, j + 1, len - 1, nums[i] + nums[j]);
if (k == -1) {
// 说明子区间 [j + 1, len - 1] 全部的数都可以构成三角形
// 其中的数的个数为 len - 1 - (j + 1) + 1
res += (len - j - 1);
} else {
// 说明子区间 [j + 1, k) 全部的数可以构成三角形,注意:这里 k 取不到
// 其中的数的个数为 k - (j + 1)
res += (k - j - 1);
}
}
}
return res;
}
private int findFirstCanNotTriangle(int[] nums, int left, int right, int target) {
// 在 nums 的子区间 [left, right] 里找第 1 个大于等于 target 的元素的索引
// 如果不存在,返回 -1
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid;
}
}
// 后处理,因为很有可能找不到大于等于 target 的元素
if (nums[left] < target) {
return -1;
}
return left;
}
}
写了从前向后的代码,从后向前的代码就好写了,不过还是要注意一些细节问题,一旦发现出错,不要着急,在编码过程中打印一些输出语句,可以帮助你调试代码。
参考代码 2:先固定 k,再固定 j,然后找 i 的下界。
Python 代码:
from typing import List
class Solution:
def triangleNumber(self, nums: List[int]) -> int:
# 索引数组:[0, 1, 2, 3, 4],size = 5
size = len(nums)
# 思路 2:从后到前,先固定 k ,再固定 j ,最后确定 i 的范围
# 首先不要忘记排序
nums.sort()
res = 0
# 注意边界,看上面那个索引数组知道 k 最小取到 2,不能再小了
for k in range(size - 1, 1, -1):
# 要给 i 留一个位置,故 1 是下限(取不到)
# print('k=', k)
for j in range(k - 1, 0, -1):
# 在区间 [0, j - 1] 中找第 1 个能构成三角形的数
# i 与 j 之间的数的个数就是一票解
# 等价于,在子区间 [0, j - 1] 里找第 1 个大于(不能等于) nums[k] - nums[j] 的数
i = self.__find_first_can_triangle(nums, 0, j - 1, nums[k] - nums[j])
# print(i, j, k)
if i == -1:
# 说明子区间 [0, j - 1] 全部的数都不能构成三角形
# 其中的数的个数为 0,
# 为了语义清晰,我还是写一下 + 0
res += 0
else:
# 说明子区间 [i, j - 1] 全部的数可以构成三角形,注意:这里 k 取不到
# 其中的数的个数为 j - 1 - i + 1
res += (j - i)
# print('res=', res)
return res
def __find_first_can_triangle(self, nums, left, right, target):
# 在 nums 的子区间 [left, right] 里找第 1 个大于(不能等于) target 的元素的索引
# 如果不存在,返回 -1
while left < right:
mid = left + (right - left) // 2
if nums[mid] <= target:
left = mid + 1
else:
right = mid
# 后处理,因为很有可能找不到大于 target 的元素
if nums[left] <= target:
return -1
return left
Java 代码:
import java.util.Arrays;
public class Solution {
public int triangleNumber(int[] nums) {
// 索引数组:[0, 1, 2, 3, 4],size = 5
// i 最多到倒数第 2 个索引
int len = nums.length;
// 思路 2:从后到前,先固定 k ,再固定 j ,最后确定 i 的范围
// 首先不要忘记排序
Arrays.sort(nums);
int res = 0;
// 注意边界,看上面那个索引数组知道 k 最小取到 2,不能再小了
for (int k = len - 1; k > 1; k--) {
// 要给 k 留一个位置,故 size - 1 是上限(取不到)
for (int j = k - 1; j > 0; j--) {
// 在区间 [0, j - 1] 中找第 1 个能构成三角形的数
// i 与 j 之间的数的个数就是一票解
// 等价于,在子区间 [0, j - 1] 里找第 1 个大于(不能等于) nums[k] - nums[j] 的数
int i = findFirstCanTriangle(nums, 0, j - 1, nums[k] - nums[j]);
if (i == -1) {
// 说明子区间 [0, j - 1] 全部的数都不能构成三角形
// 其中的数的个数为 0,
// 为了语义清晰,我还是写一下 + 0
res += 0;
} else {
// 说明子区间 [i, j - 1] 全部的数可以构成三角形,注意:这里 k 取不到
// 其中的数的个数为 j - 1 - i + 1
res += (j - i);
}
}
}
return res;
}
private int findFirstCanTriangle(int[] nums, int left, int right, int target) {
// 在 nums 的子区间 [left, right] 里找第 1 个大于(不能等于) target 的元素的索引
// 如果不存在,返回 -1
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] <= target) {
left = mid + 1;
} else {
right = mid;
}
}
// 后处理,因为很有可能找不到大于等于 target 的元素
if (nums[left] <= target) {
return -1;
}
return left;
}
}
总结:两种方法写下来,个人还是推荐“从前向后”的办法,正向思维不太容易出错。