LeetCode 第 450 题:“删除二叉搜索树中的节点”题解
题解地址:用前驱或者后继结点代替被删除结点(Python、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:450. 删除二叉搜索树中的节点。
用前驱或者后继结点代替被删除结点(Python、Java 代码)
“二分搜索树删除结点”这一操作在《数据结构与算法》这一类的教科书上均有介绍,虽然这个操作是计算机科学家 Hibbard 发明的,但其实这个操作非常简单且直观。
掌握递归删除二分搜索树结点的方法,注意递归函数的定义,有的时候需要返回一个新的二分搜索树的根。
思路分析
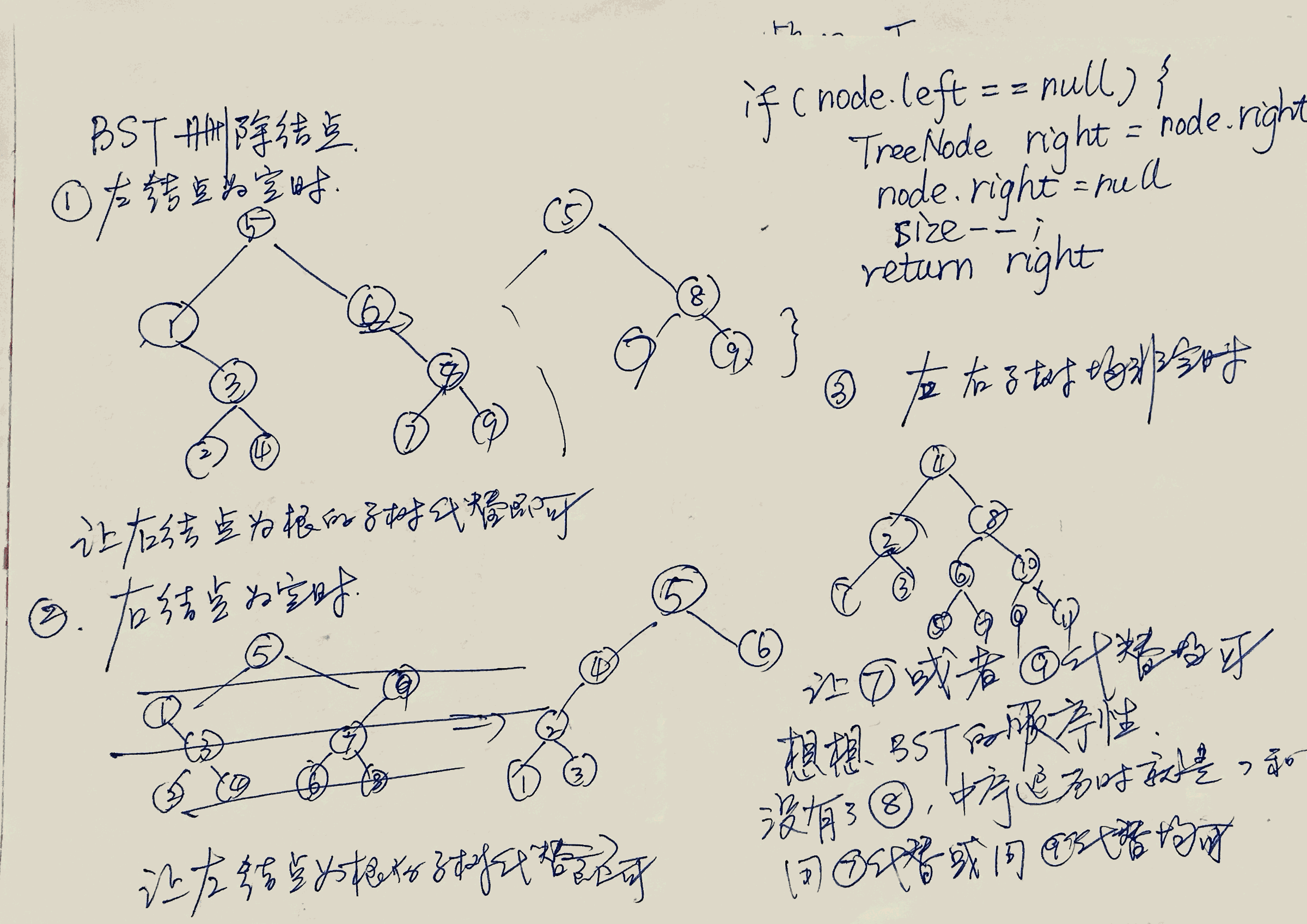
理解这个算法的关键在于保持 BST 中序遍历的顺序性,当待删除结点的左右结点都不为空的时候,让待删除结点的前驱结点或者后继结点代替被删除结点,这样就能成为一棵树,并且还是 BST,否则就变成森林,或者不保持 BST 中序遍历的顺序性了。
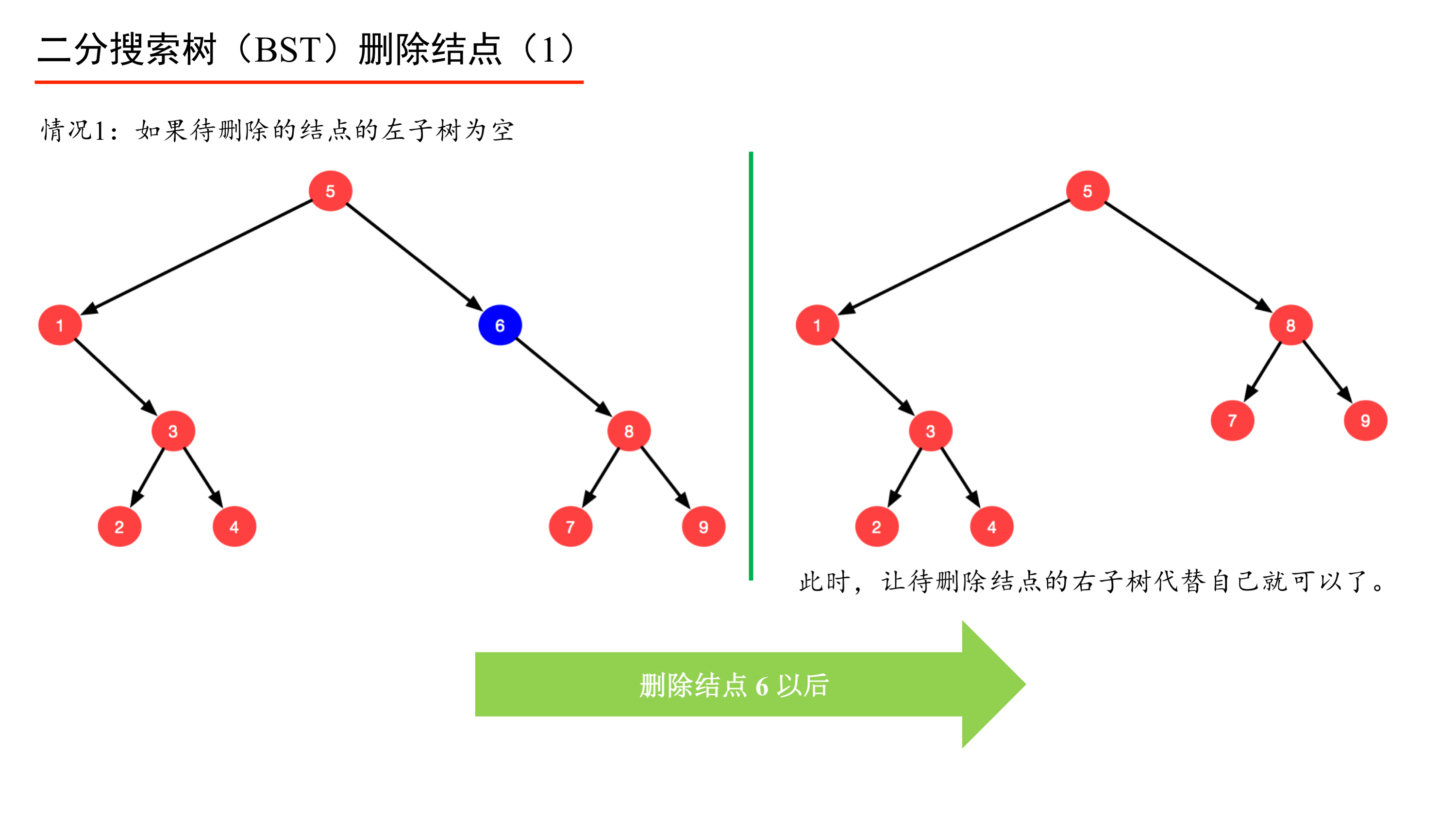
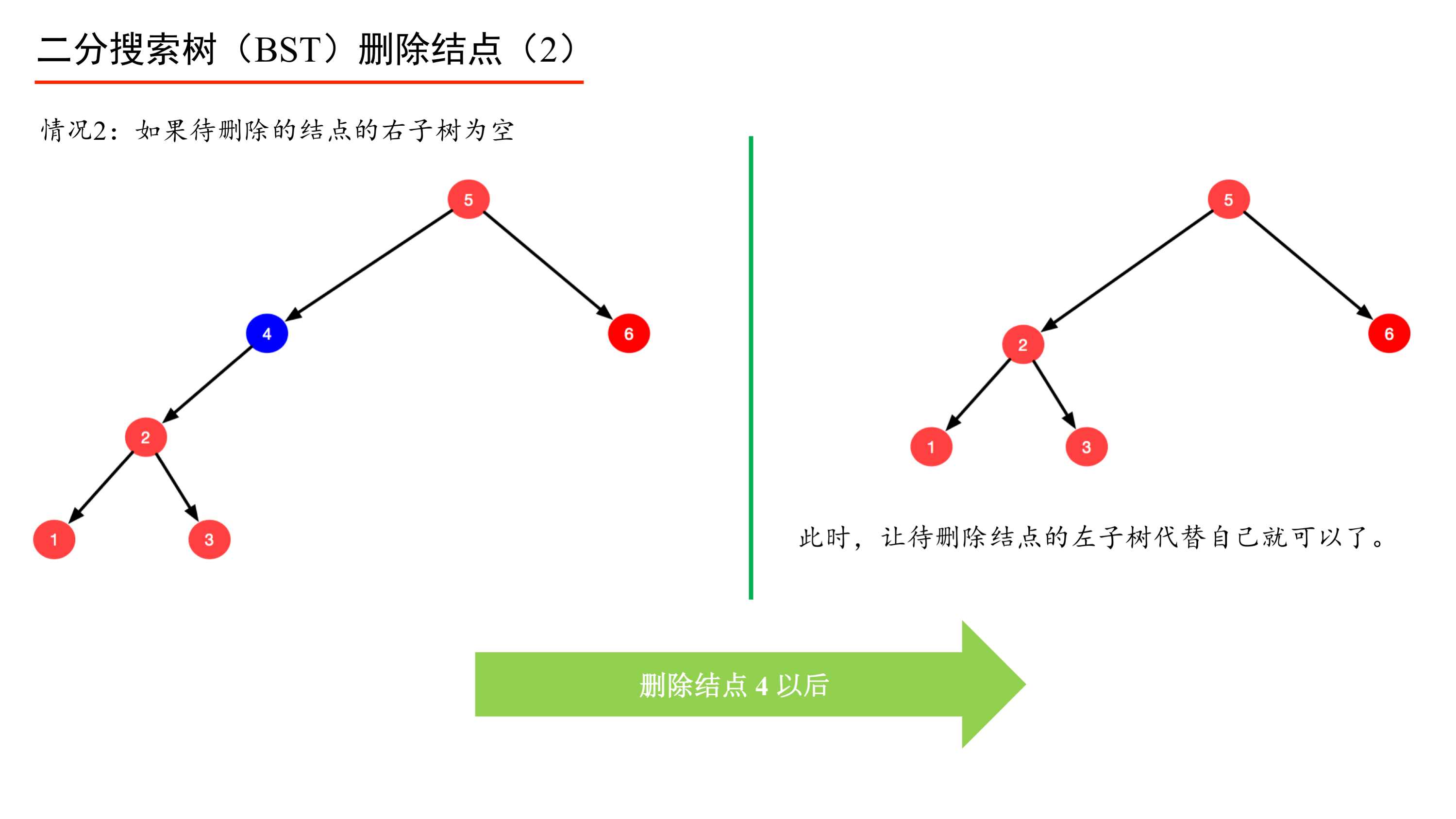
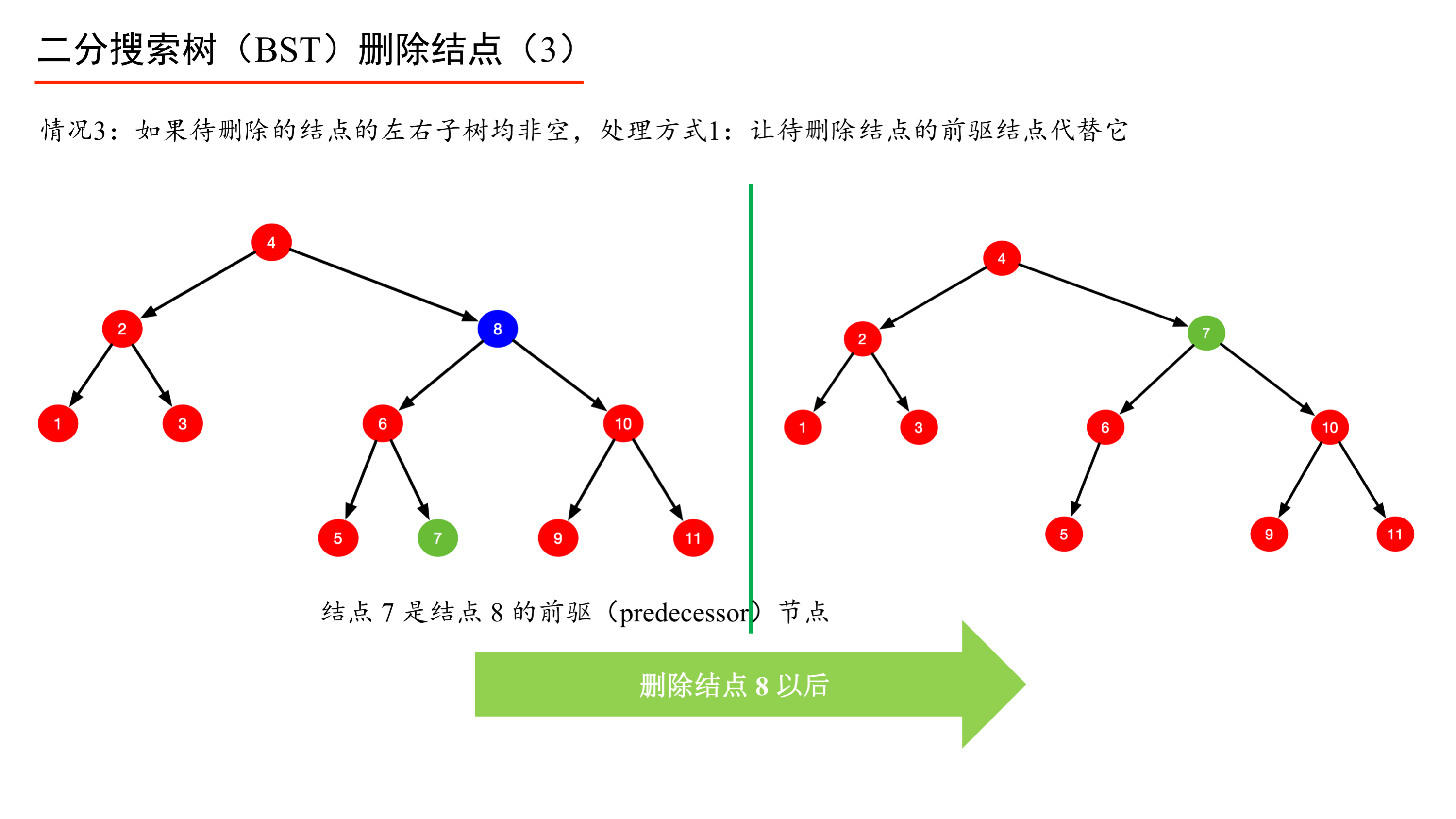
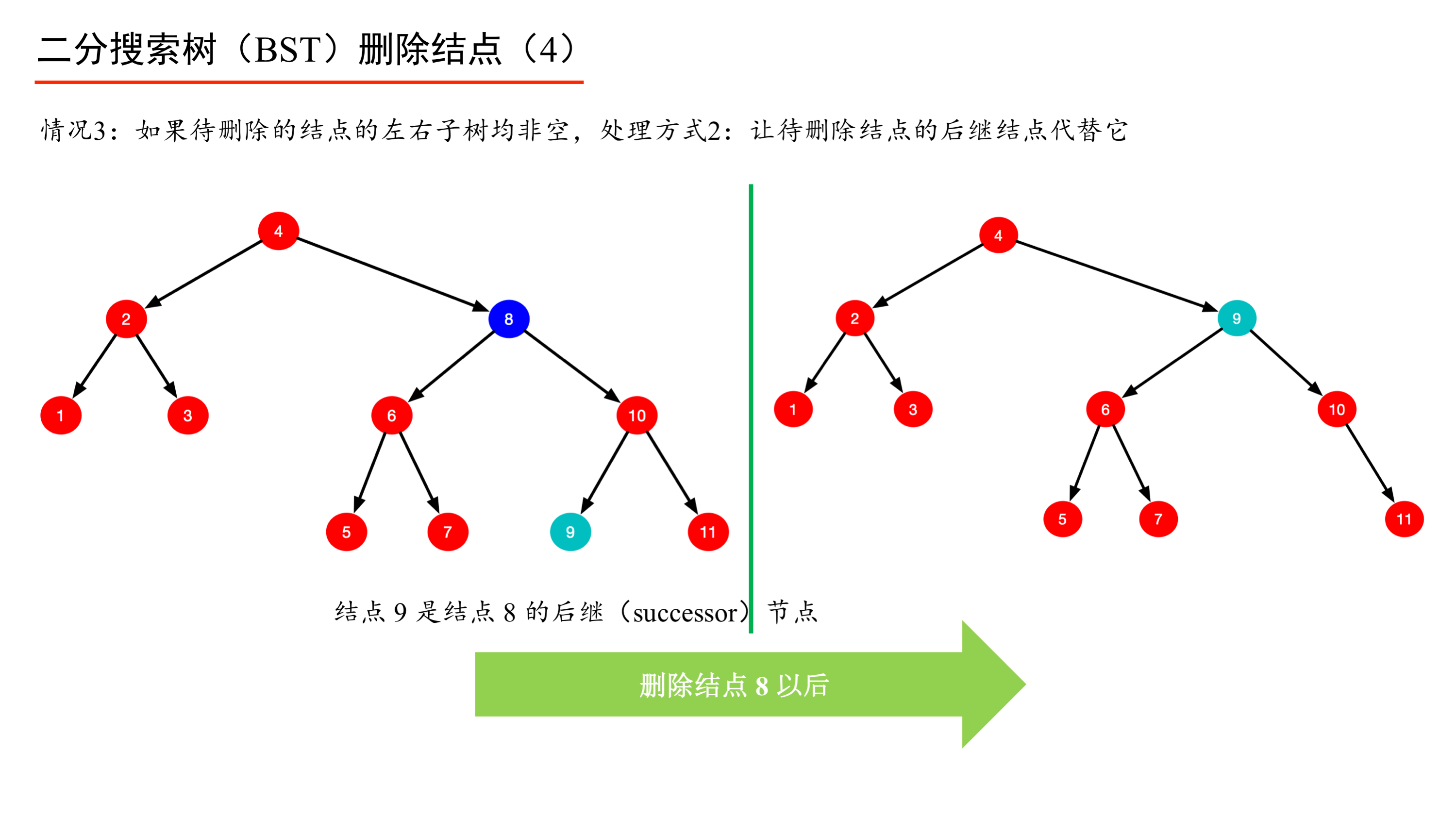
在草稿纸上很容易画出 BST 删除结点操作的这 3 种情况。

方法一:用前驱结点(左子树中最大结点)代替被删除结点
参考代码 1:
Python 代码:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
# 方法1:用左子树中最大结点的代替被删除结点
class Solution:
def deleteNode(self, root, key):
if root is None:
return None
if key < root.val:
root.left = self.deleteNode(root.left, key)
return root
if key > root.val:
root.right = self.deleteNode(root.right, key)
return root
if root.left is None:
new_root = root.right
root.right = None
return new_root
if root.right is None:
new_root = root.left
root.left = None
return new_root
# 找到左子树中最大的
predecessor = self.__maximum(root.left)
predecessor_copy = TreeNode(predecessor.val)
predecessor_copy.left = self.__remove_max(root.left)
predecessor_copy.right = root.right
root.left = None
root.right = None
return predecessor_copy
def __remove_max(self, node):
if node.right is None:
new_root = node.left
node.left = None
return new_root
node.right = self.__remove_max(node.right)
return node
def __maximum(self, node):
while node.right:
node = node.right
return node
Java 代码:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
}
if (key < root.val) {
root.left = deleteNode(root.left, key);
return root;
}
if (key > root.val) {
root.right = deleteNode(root.right, key);
return root;
}
assert key == root.val;
if (root.left == null) {
TreeNode right = root.right;
root.right = null;
return right;
}
if (root.right == null) {
TreeNode left = root.left;
root.left = null;
return left;
}
TreeNode predecessor = maximum(root.left);
TreeNode predecessorCopy = new TreeNode(predecessor.val);
predecessorCopy.left = removeMax(root.left);
predecessorCopy.right = root.right;
root.left = null;
root.right = null;
return predecessorCopy;
}
private TreeNode removeMax(TreeNode node) {
if (node.right == null) {
TreeNode left = node.left;
node.left = null;
return left;
}
node.right = removeMax(node.right);
return node;
}
private TreeNode maximum(TreeNode node) {
if (node.right == null) {
return node;
}
return maximum(node.right);
}
}
方法二:用后继结点(右子树中最小结点)代替被删除结点
参考代码 2:
Python 代码:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
# 方法2:用右子树中最小结点的代替被删除结点
class Solution:
def deleteNode(self, root, key):
if root is None:
return None
if key < root.val:
root.left = self.deleteNode(root.left, key)
return root
if key > root.val:
root.right = self.deleteNode(root.right, key)
return root
if root.left is None:
new_root = root.right
root.right = None
return new_root
if root.right is None:
new_root = root.left
root.left = None
return new_root
# 找到右子树中最小的结点,复制它的值
successor = self.__minimum(root.right)
successor_copy = TreeNode(successor.val)
successor_copy.left = root.left
successor_copy.right = self.__remove_min(root.right)
root.left = None
root.right = None
return successor_copy
def __remove_min(self, node):
if node.left is None:
new_root = node.right
node.right = None
return new_root
node.left = self.__remove_min(node.left)
return node
def __minimum(self, node):
while node.left:
node = node.left
return node
Java 代码:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution {
private TreeNode minNode(TreeNode node) {
while (node.left != null) {
node = node.left;
}
return node;
}
/**
* 删除一个二分搜索树中最小的节点,把新的二分搜索树的根返回回去
* 使用递归,要特别注意,定义的递归函数,返回的是,删除了最小值节点以后的新的二分搜索树的根
*
* @param node
* @return
*/
private TreeNode removeMin(TreeNode node) {
if (node.left == null) {
// 就是那个我们要删除的节点
TreeNode rightNode = node.right;
node.right = null;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
}
if (root.val < key) {
root.right = deleteNode(root.right, key);
return root;
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
return root;
} else {
// 如果待删除的节点左孩子为空
if (root.left == null) {
TreeNode rightNode = root.right;
root.right = null;
return rightNode;
}
// 如果待删除的节点只有右孩子
if (root.right == null) {
TreeNode leftNode = root.left;
root.left = null;
return leftNode;
}
// 从它的右子树中拿到最小的
TreeNode successor = new TreeNode(minNode(root.right).val);
successor.left = root.left;
successor.right = removeMin(root.right);
root.left = null;
root.right = null;
return successor;
}
}
}