LeetCode 第 295 题:“数据流的中位数”题解
题解地址:优先队列(Python 代码、Java 代码)。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门:295. 数据流的中位数。
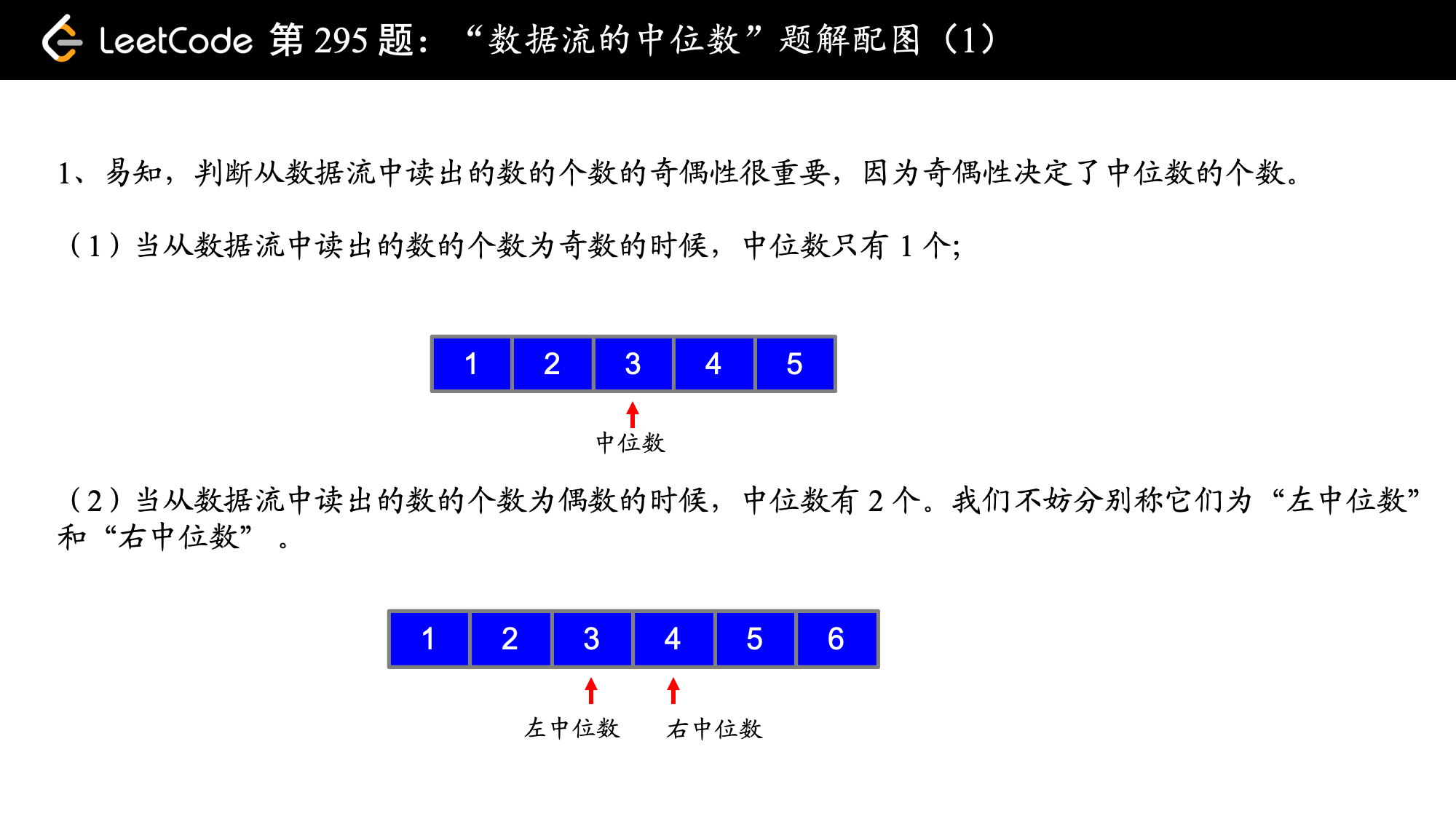
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。 double findMedian() - 返回目前所有元素的中位数。 示例:
addNum(1) addNum(2) findMedian() -> 1.5 addNum(3) findMedian() -> 2 进阶:
如果数据流中所有整数都在 0 到 100 范围内,你将如何优化你的算法? 如果数据流中 99% 的整数都在 0 到 100 范围内,你将如何优化你的算法?
优先队列(Python 代码、Java 代码)
思路分析:
一种最容易想到的思路是,数据流新进来一个数,都把它与已经读出来的数进行一次排序,这样中位数就可以很容易得到。这样做“不好”的地方是:
排序的时间复杂度为 ,但事实上,我对除了中位数以外的其它位置的元素并不关心。
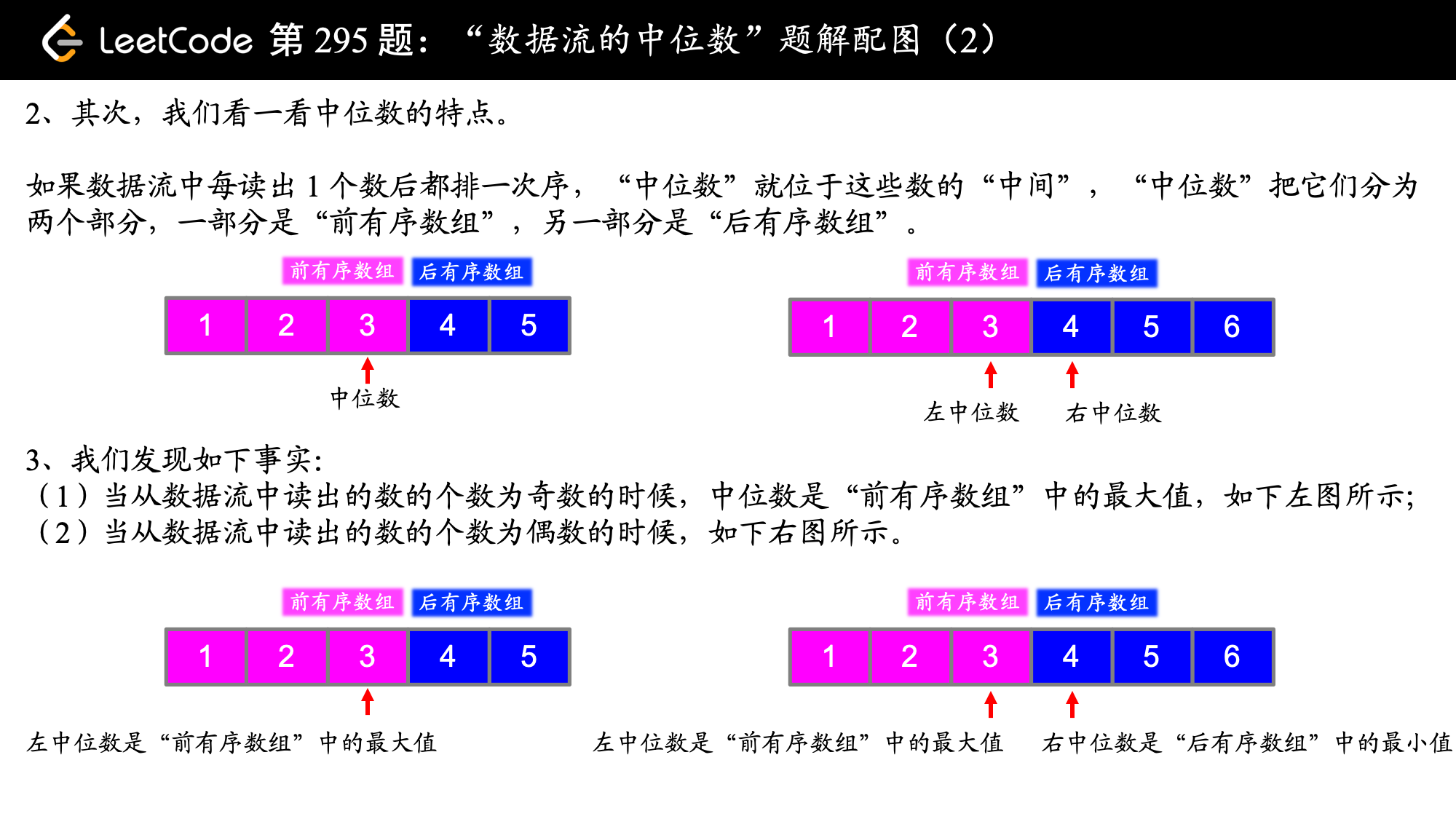
事实上,我们只关心在中间的那两个数(或者一个数),其它数没有必要进行 “比较” 和 “交换” 的操作。
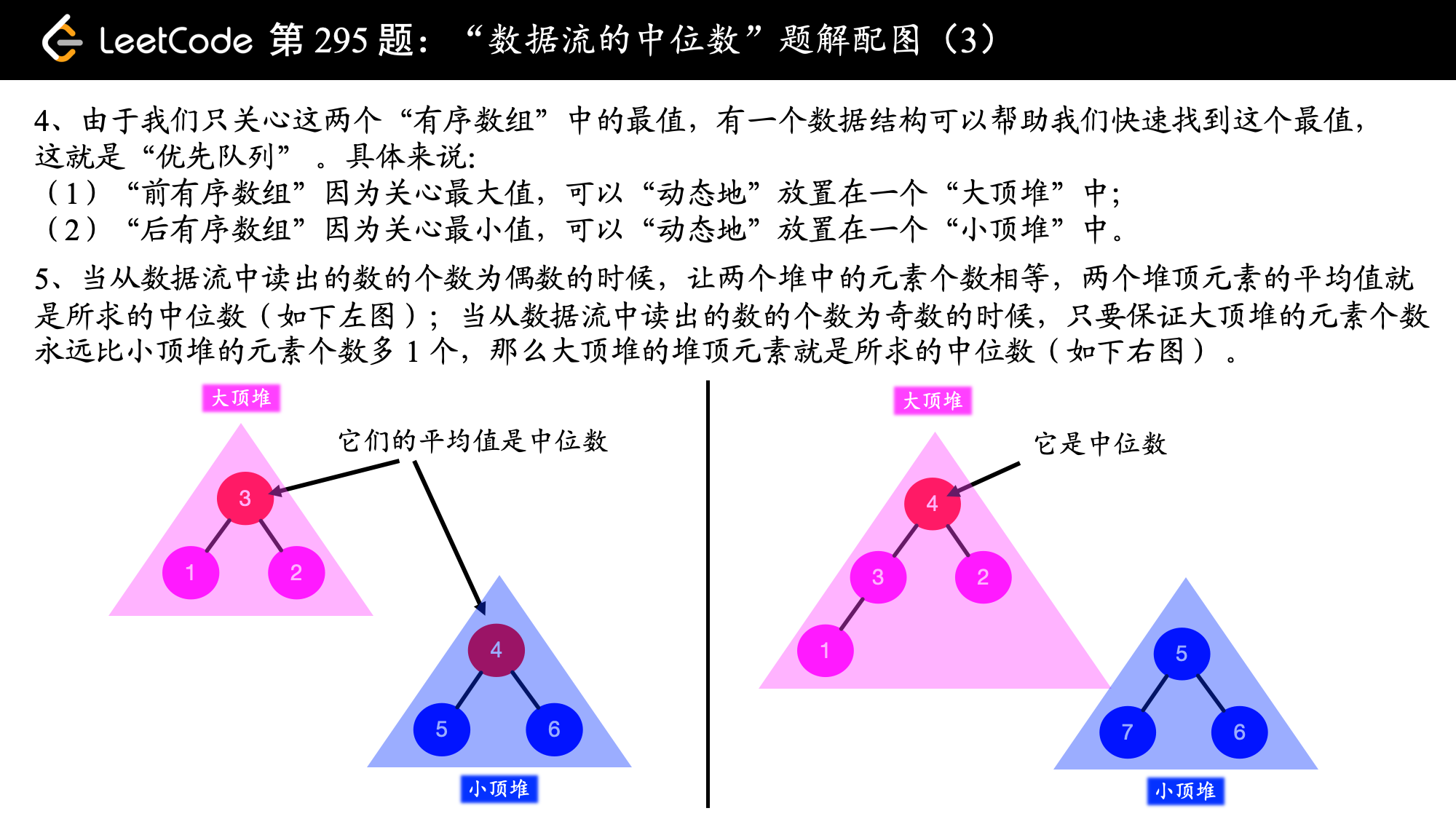
在我们学习过的数据结构里,堆就有类似的性质,每次都从堆里得到一个 “最值” 而其它元素无需排序,这样就可以以 的复杂度每次都从堆中取出最值。
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
 ,
, ,
, ,
,
请读者在看完以上思路之后思考:
1、数据是如何在两个堆之间流动的,脑子里要建立如下动态的过程:为了找到添加新数据以后,数据流的中位数,我们让这个新数据在大顶堆和小顶堆中都走了一遍。而为了让大顶堆的元素多 个,我们让从小顶堆中又拿出一个元素“送回”给大顶堆;
2、将元素放入优先队列以后,优先队列会以对数时间复杂度自行调整,把“最优值”放入堆顶,这是使用优先队列解决这个问题的原因。如果不太熟悉优先队列的朋友们,请复习一下优先队列的相关知识,包括基本操作,理解上浮和下沉。
说明: 这道题使用 Java 编码看起来思路更清晰一些,在 Python 中的堆只有小顶堆,在构造大顶堆的时候,要绕一个弯子,具体请看如下参考代码。
参考代码:
Java 代码:
import java.util.PriorityQueue;
public class MedianFinder {
/**
* 当前大顶堆和小顶堆的元素个数之和
*/
private int count;
private PriorityQueue<Integer> maxheap;
private PriorityQueue<Integer> minheap;
/**
* initialize your data structure here.
*/
public MedianFinder() {
count = 0;
maxheap = new PriorityQueue<>((x, y) -> y - x);
minheap = new PriorityQueue<>();
}
public void addNum(int num) {
count += 1;
maxheap.offer(num);
minheap.add(maxheap.poll());
// 如果两个堆合起来的元素个数是奇数,小顶堆要拿出堆顶元素给大顶堆
if ((count & 1) != 0) {
maxheap.add(minheap.poll());
}
}
public double findMedian() {
if ((count & 1) == 0) {
// 如果两个堆合起来的元素个数是偶数,数据流的中位数就是各自堆顶元素的平均值
return (double) (maxheap.peek() + minheap.peek()) / 2;
} else {
// 如果两个堆合起来的元素个数是奇数,数据流的中位数大顶堆的堆顶元素
return (double) maxheap.peek();
}
}
}
Python 代码:
import heapq
class MedianFinder:
def __init__(self):
# 当前大顶堆和小顶堆的元素个数之和
self.count = 0
self.max_heap = []
self.min_heap = []
def addNum(self, num: int) -> None:
self.count += 1
# 因为 Python 中的堆默认是小顶堆,所以要传入一个 tuple,用于比较的元素需是相反数,
# 才能模拟出大顶堆的效果
heapq.heappush(self.max_heap, (-num, num))
_, max_heap_top = heapq.heappop(self.max_heap)
heapq.heappush(self.min_heap, max_heap_top)
if self.count & 1:
min_heap_top = heapq.heappop(self.min_heap)
heapq.heappush(self.max_heap, (-min_heap_top, min_heap_top))
def findMedian(self) -> float:
if self.count & 1:
# 如果两个堆合起来的元素个数是奇数,数据流的中位数大顶堆的堆顶元素
return self.max_heap[0][1]
else:
# 如果两个堆合起来的元素个数是偶数,数据流的中位数就是各自堆顶元素的平均值
return (self.min_heap[0] + self.max_heap[0][1]) / 2
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()
复杂度分析:
时间复杂度:,优先队列的出队入队操作都是对数级别的,数据在两个堆中间来回操作是常数级别的,综上时间复杂度是 级别的。
空间复杂度:,使用了三个辅助空间,其中两个堆的空间复杂度是 O(\cfrac{N}{2}),一个表示数据流元素个数的计数器
count,占用空间 ,综上空间复杂度为 。
使用自己实现的“大顶堆” 和 “小顶堆”
以下内容仅供参考。
下面给出一个使用 Python 从“上浮”和“下沉”底层操作,“大顶堆” 和 “小顶堆” 的实现的示例代码,目的是为了验证自己写的 “大顶堆” 和 “小顶堆” 是否正确。
从底层编写“优先队列”的步骤,可以参考我的笔记 《【算法日积月累】9-堆与优先队列》 ,特别欢迎您给出意见和建议。
为了验证自己写的底层代码是否正确,把自己写的底层数据结构用于完成 LeetCode 的问题,让自己的数据结构经过 LeetCode 测试用例的检测,是一个很不错的办法。
参考代码 2:
Python 代码:
class MaxHeap:
def __init__(self, capacity):
# 我们这个版本的实现中,0 号索引是不存数据的,这一点一定要注意
# 因为数组从索引 1 开始存放数值
# 所以开辟 capacity + 1 这么多大小的空间
self.data = [None for _ in range(capacity + 1)]
# 当前堆中存储的元素的个数
self.count = 0
# 堆中能够存储的元素的最大数量(为简化问题,不考虑动态扩展)
self.capacity = capacity
def size(self):
"""
返回最大堆中的元素的个数
:return:
"""
return self.count
def is_empty(self):
"""
返回最大堆中的元素是否为空
:return:
"""
return self.count == 0
def insert(self, item):
if self.count + 1 > self.capacity:
raise Exception('堆的容量不够了')
self.count += 1
self.data[self.count] = item
# 考虑将它上移
self.__swim(self.count)
def __shift_up(self, k):
# 有索引就要考虑索引越界的情况,已经在索引 1 的位置,就没有必要上移了
while k > 1 and self.data[k // 2] < self.data[k]:
self.data[k // 2], self.data[k] = self.data[k], self.data[k // 2]
k //= 2
def __swim(self, k):
# 上浮,与父结点进行比较
temp = self.data[k]
# 有索引就要考虑索引越界的情况,已经在索引 1 的位置,就没有必要上移了
while k > 1 and self.data[k // 2] < temp:
self.data[k] = self.data[k // 2]
k //= 2
self.data[k] = temp
def extract_max(self):
if self.count == 0:
raise Exception('堆里没有可以取出的元素')
ret = self.data[1]
self.data[1], self.data[self.count] = self.data[self.count], self.data[1]
self.count -= 1
self.__sink(1)
return ret
def __shift_down(self, k):
# 只要有左右孩子,左右孩子只要比自己大,就交换
while 2 * k <= self.count:
# 如果这个元素有左边的孩子
j = 2 * k
# 如果有右边的孩子,大于左边的孩子,就好像左边的孩子不存在一样
if j + 1 <= self.count and self.data[j + 1] > self.data[j]:
j = j + 1
if self.data[k] >= self.data[j]:
break
self.data[k], self.data[j] = self.data[j], self.data[k]
k = j
def __sink(self, k):
# 下沉
temp = self.data[k]
# 只要它有孩子,注意,这里的等于号是十分关键的
while 2 * k <= self.count:
j = 2 * k
# 如果它有右边的孩子,并且右边的孩子大于左边的孩子
if j + 1 <= self.count and self.data[j + 1] > self.data[j]:
# 右边的孩子胜出,此时可以认为没有左孩子
j += 1
# 如果当前的元素的值,比右边的孩子节点要大,则逐渐下落的过程到此结束
if temp >= self.data[j]:
break
# 否则,交换位置,继续循环
self.data[k] = self.data[j]
k = j
self.data[k] = temp
class MinHeap:
# 把最大堆实现中不等号的方向反向就可以了
def __init__(self, capacity):
# 因为数组从索引 1 开始存放数值
# 所以开辟 capacity + 1 这么多大小的空间
self.data = [0 for _ in range(capacity + 1)]
self.count = 0
self.capacity = capacity
def size(self):
return self.count
def is_empty(self):
return self.count == 0
def insert(self, item):
if self.count + 1 > self.capacity:
raise Exception('堆的容量不够了')
self.count += 1
self.data[self.count] = item
self.__swim(self.count)
def __swim(self, k):
# 上浮,与父节点进行比较
temp = self.data[k]
while k > 1 and self.data[k // 2] > temp:
self.data[k] = self.data[k // 2]
k //= 2
self.data[k] = temp
def extract_min(self):
if self.count == 0:
raise Exception('堆里没有可以取出的元素')
ret = self.data[1]
self.data[1] = self.data[self.count]
self.count -= 1
self.__sink(1)
return ret
def __sink(self, k):
# 下沉
temp = self.data[k]
while 2 * k <= self.count:
j = 2 * k
if j + 1 <= self.count and self.data[j + 1] < self.data[j]:
j += 1
if temp <= self.data[j]:
break
self.data[k] = self.data[j]
k = j
self.data[k] = temp
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
# 如果测试用例的容量增加,下面 10000 这个数值请大家自行调整
self.max_heap = MaxHeap(10000)
self.min_heap = MinHeap(10000)
def addNum(self, num: 'int') -> 'None':
# 大顶堆先进一个元素
self.max_heap.insert(num);
# 然后从大顶堆里出一个元素到小顶堆
self.min_heap.insert(self.max_heap.extract_max())
if self.max_heap.size() < self.min_heap.size():
# 如果大顶堆的元素少于小顶堆
# 就要从小顶堆出一个元素到大顶堆
self.max_heap.insert(self.min_heap.extract_min())
def findMedian(self) -> 'float':
if self.max_heap.size() == self.min_heap.size():
return (self.max_heap.data[1] + self.min_heap.data[1]) / 2
else:
return self.max_heap.data[1]
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()