LeetCode 题解

LeetCode 第 79 题：“单词搜索”题解

题解地址：在二维平面上使用回溯法（Python 代码、Java 代码）。

说明：文本首发在力扣的题解版块，更新也会在第 1 时间在上面的网站中更新，这篇文章只是上面的文章的一个快照，您可以点击上面的链接看到其他网友对本文的评论。

传送门：79. 单词搜索。

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

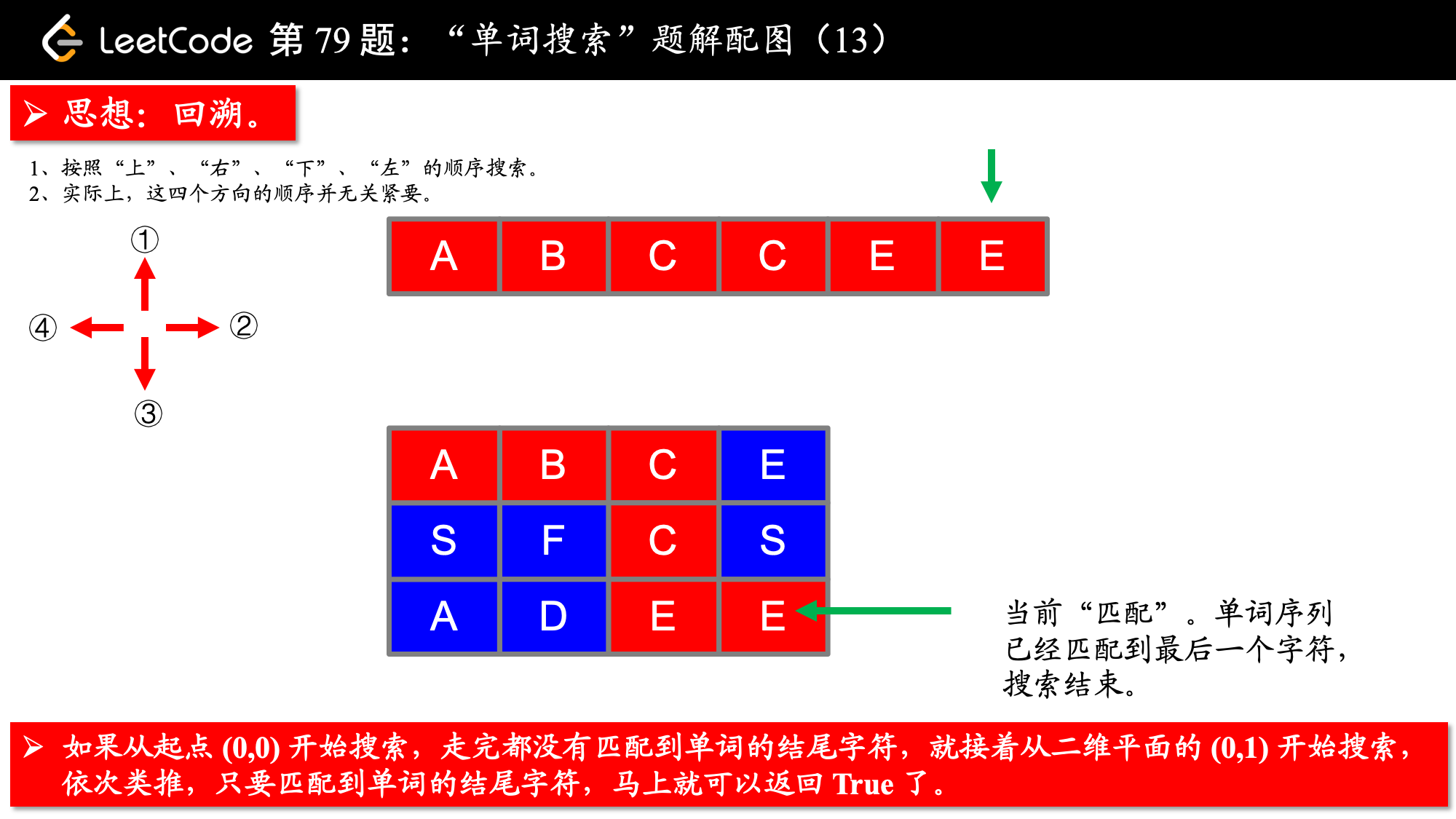
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

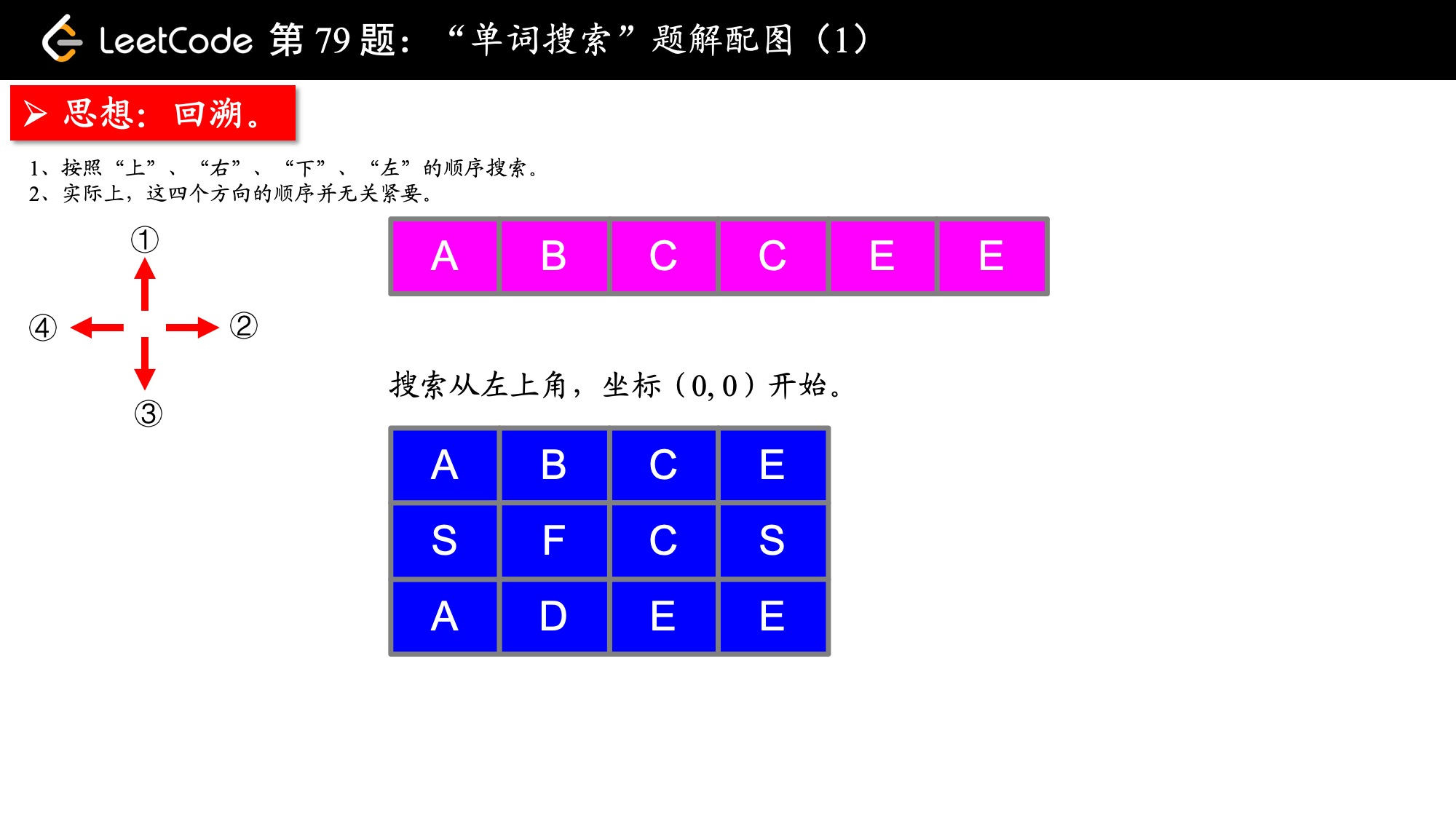
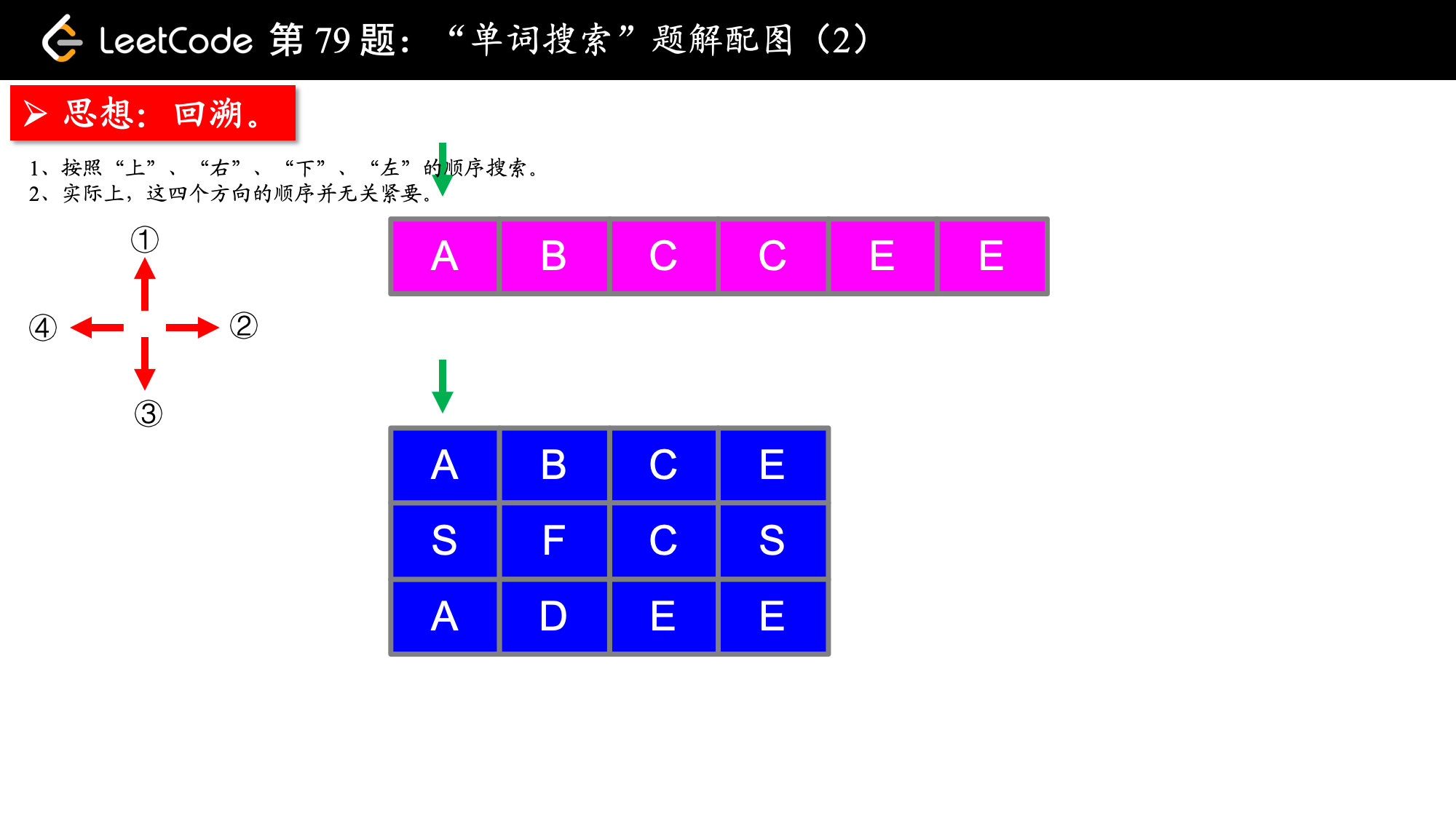
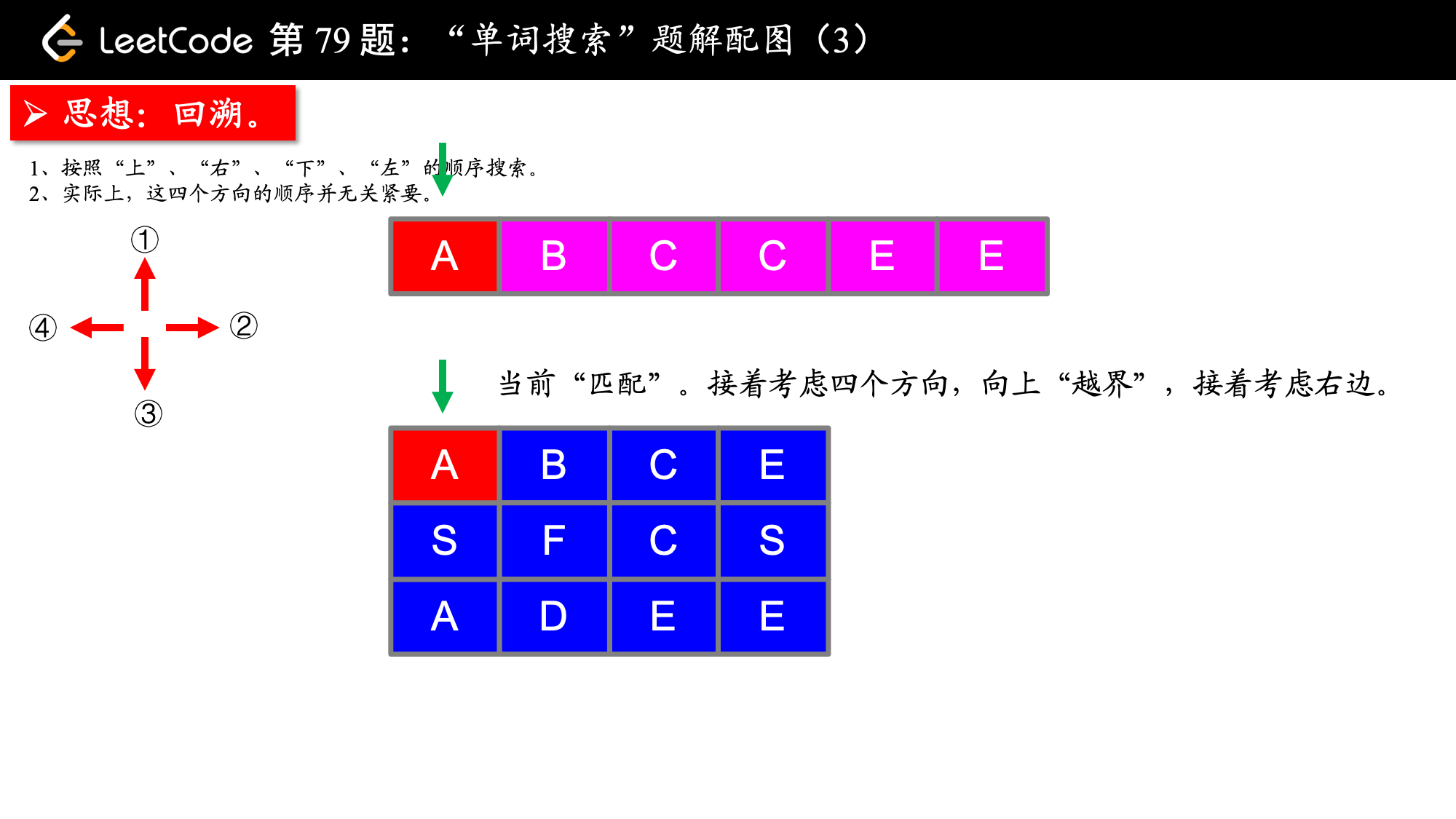
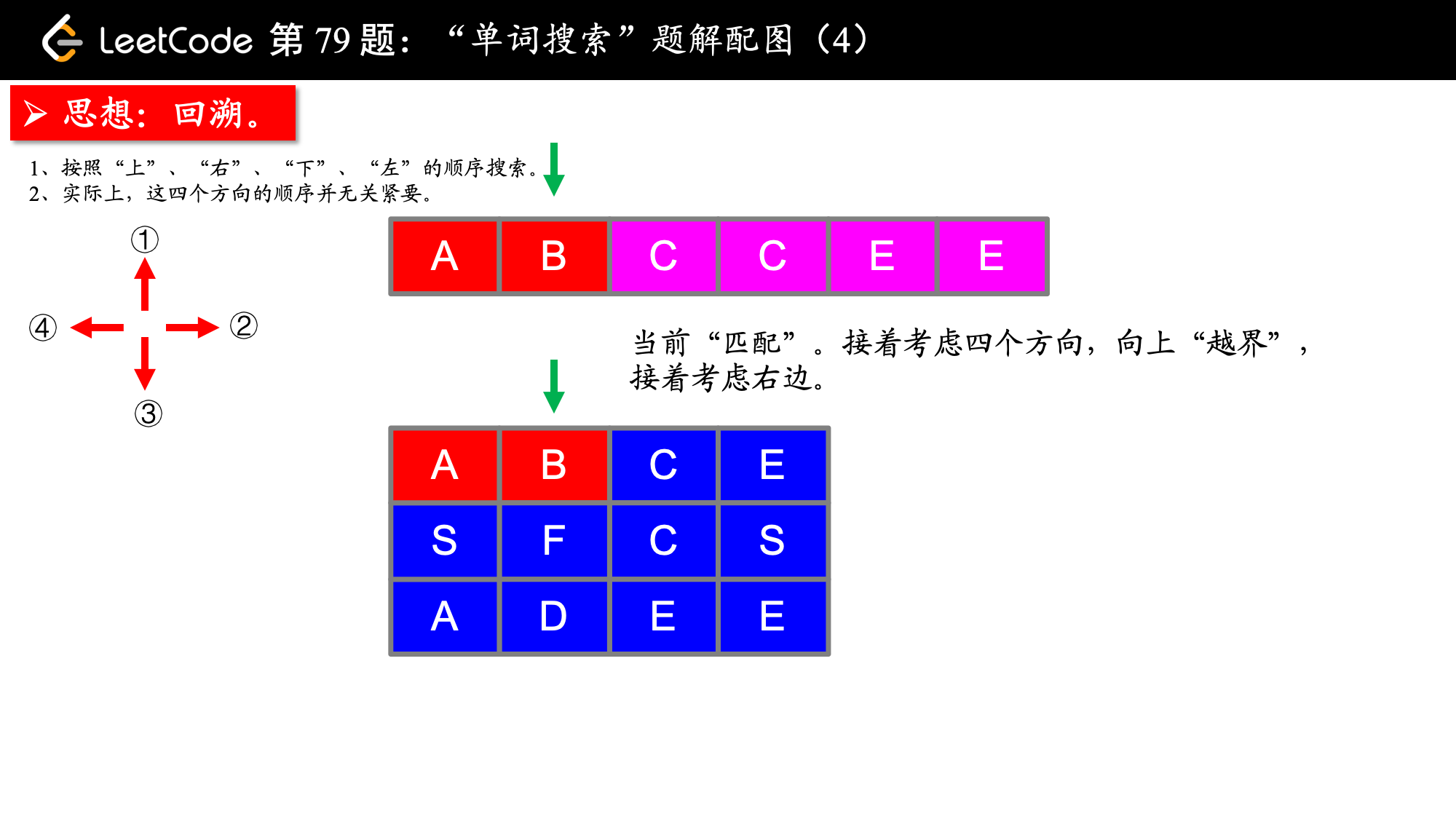
board = [ ['A','B','C','E'], ['S','F','C','S'], ['A','D','E','E'] ]

给定 word = "ABCCED", 返回 true. 给定 word = "SEE", 返回 true. 给定 word = "ABCB", 返回 false.

在二维平面上使用回溯法（Python 代码、Java 代码）

这是一个使用回溯算法解决的问题，涉及的知识点有 DFS 和状态重置。

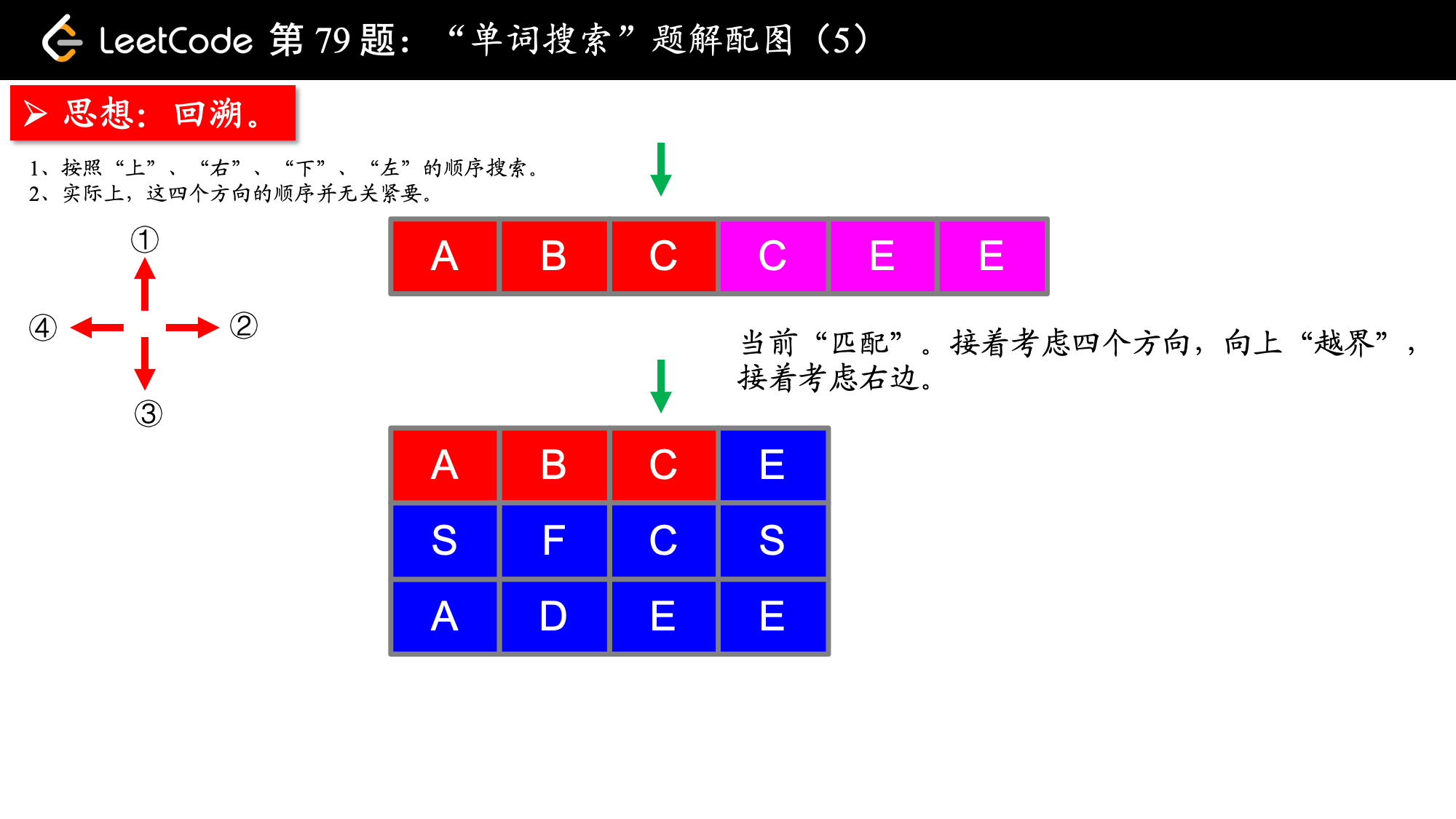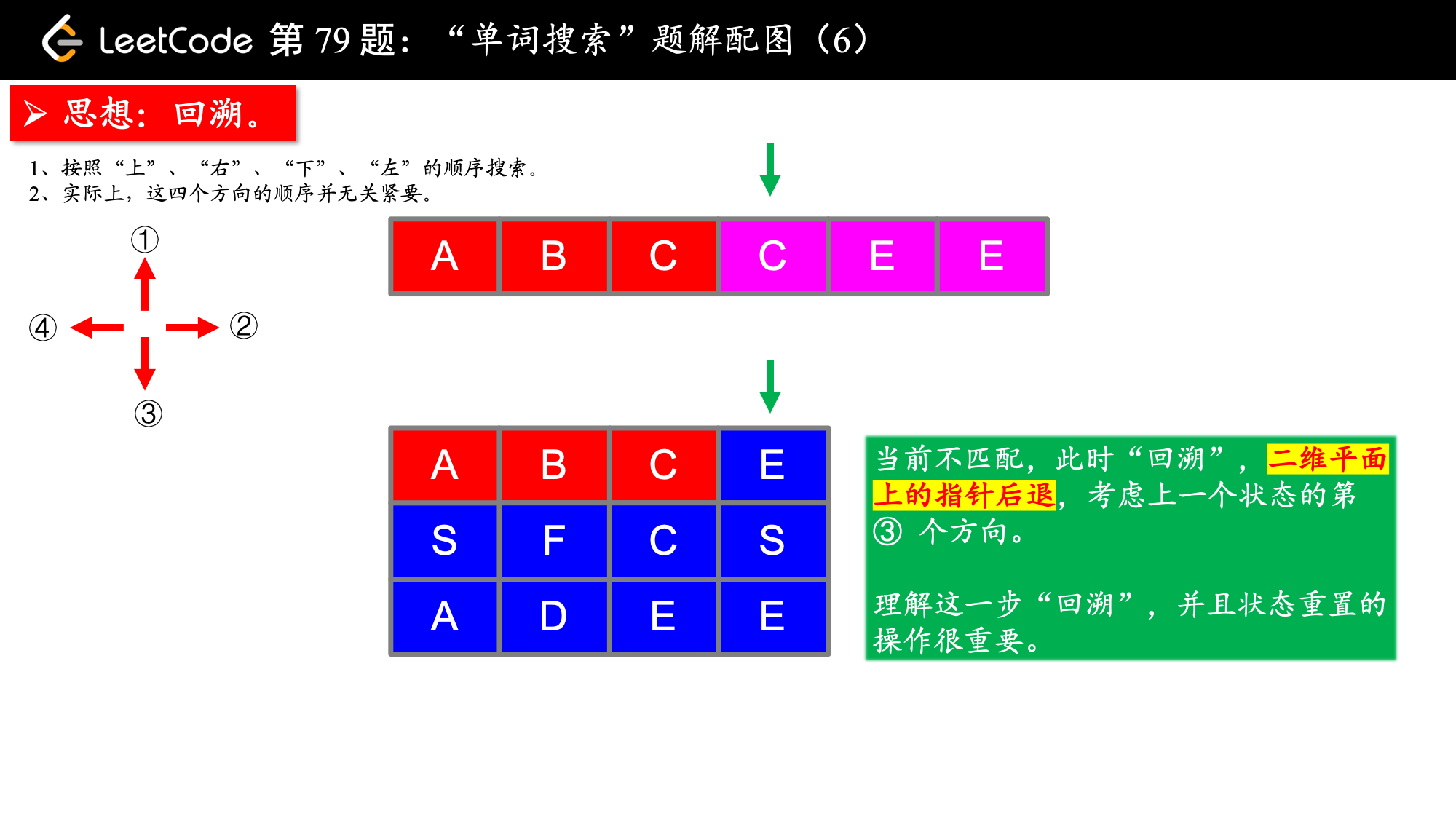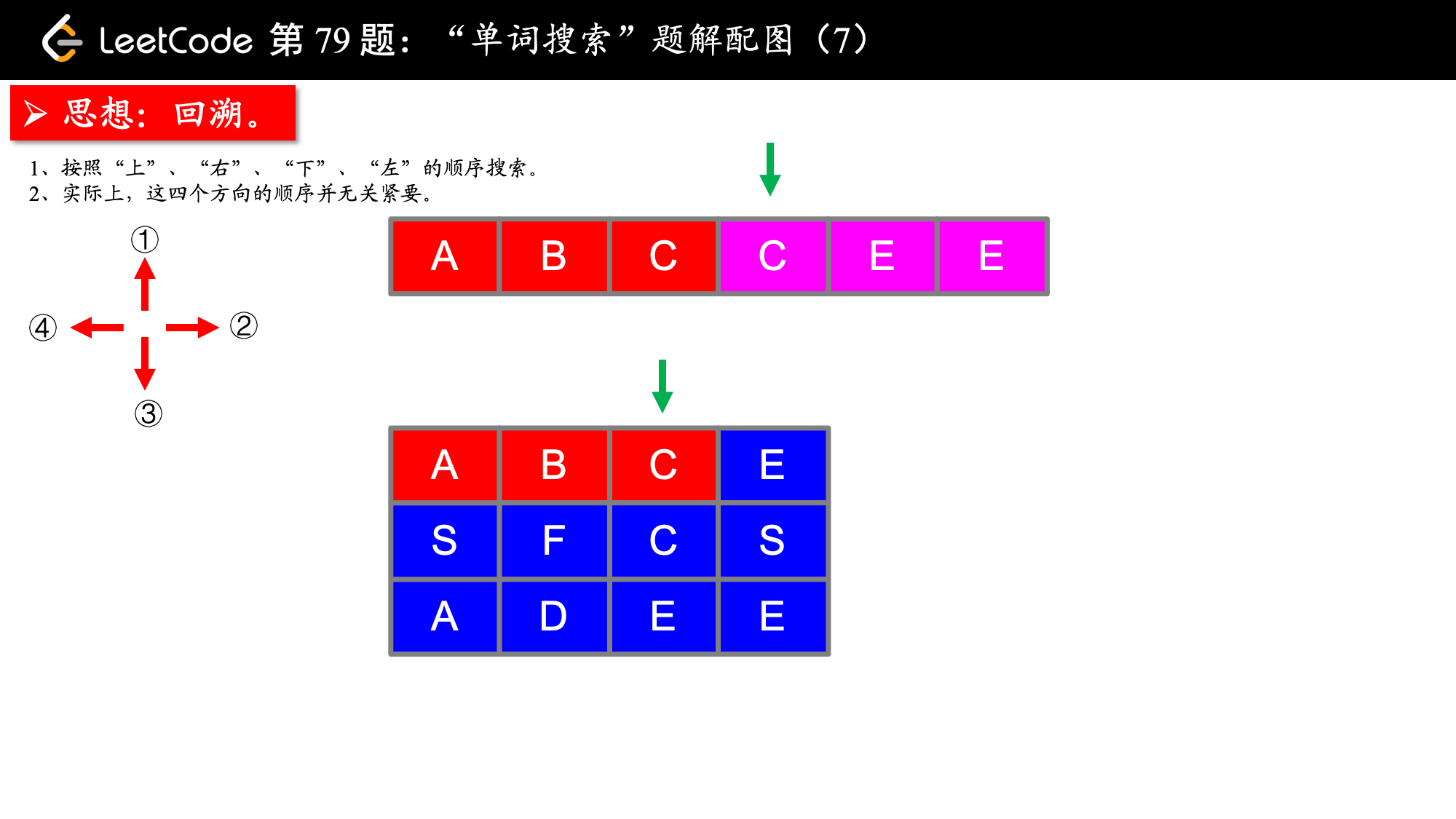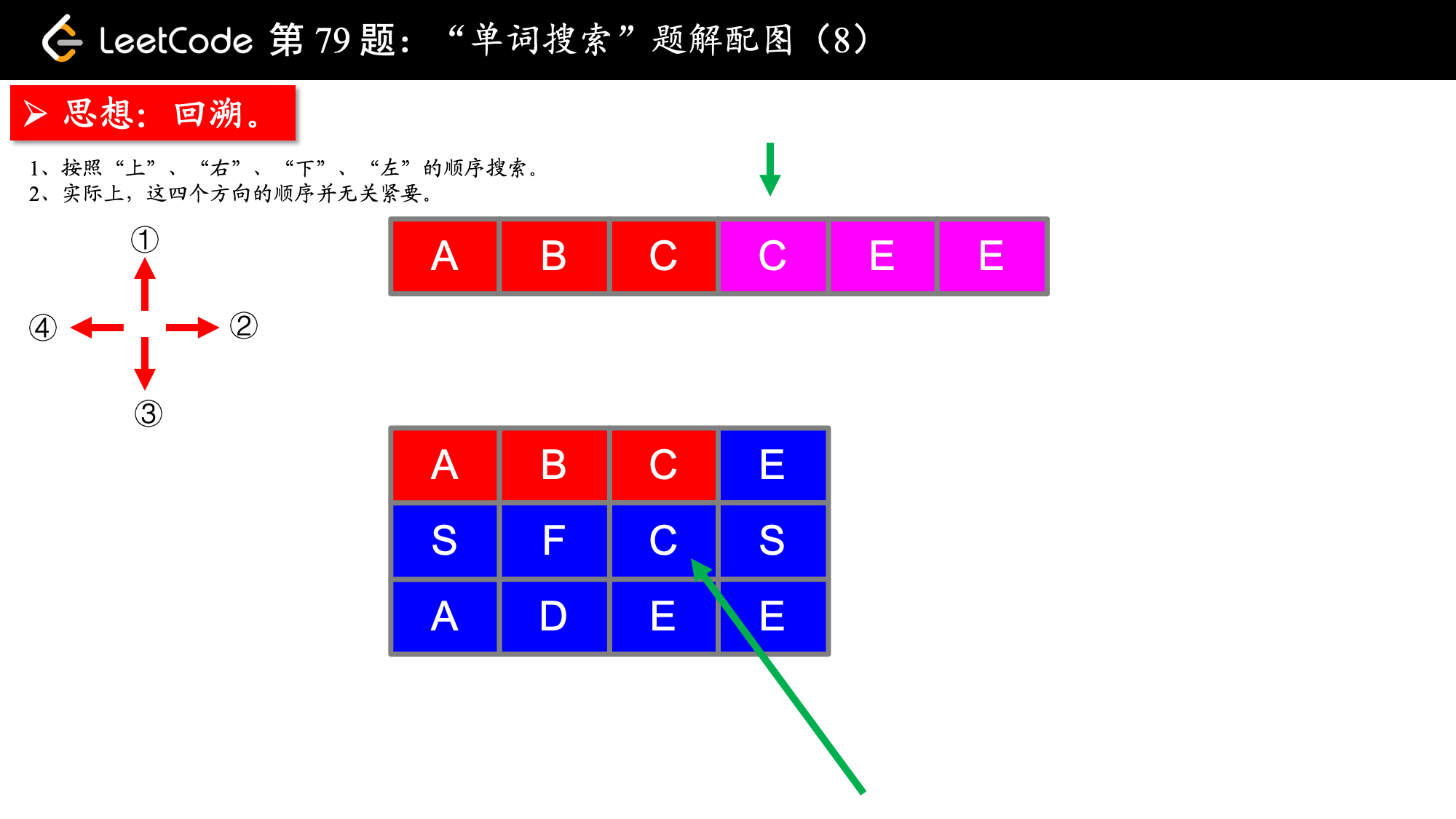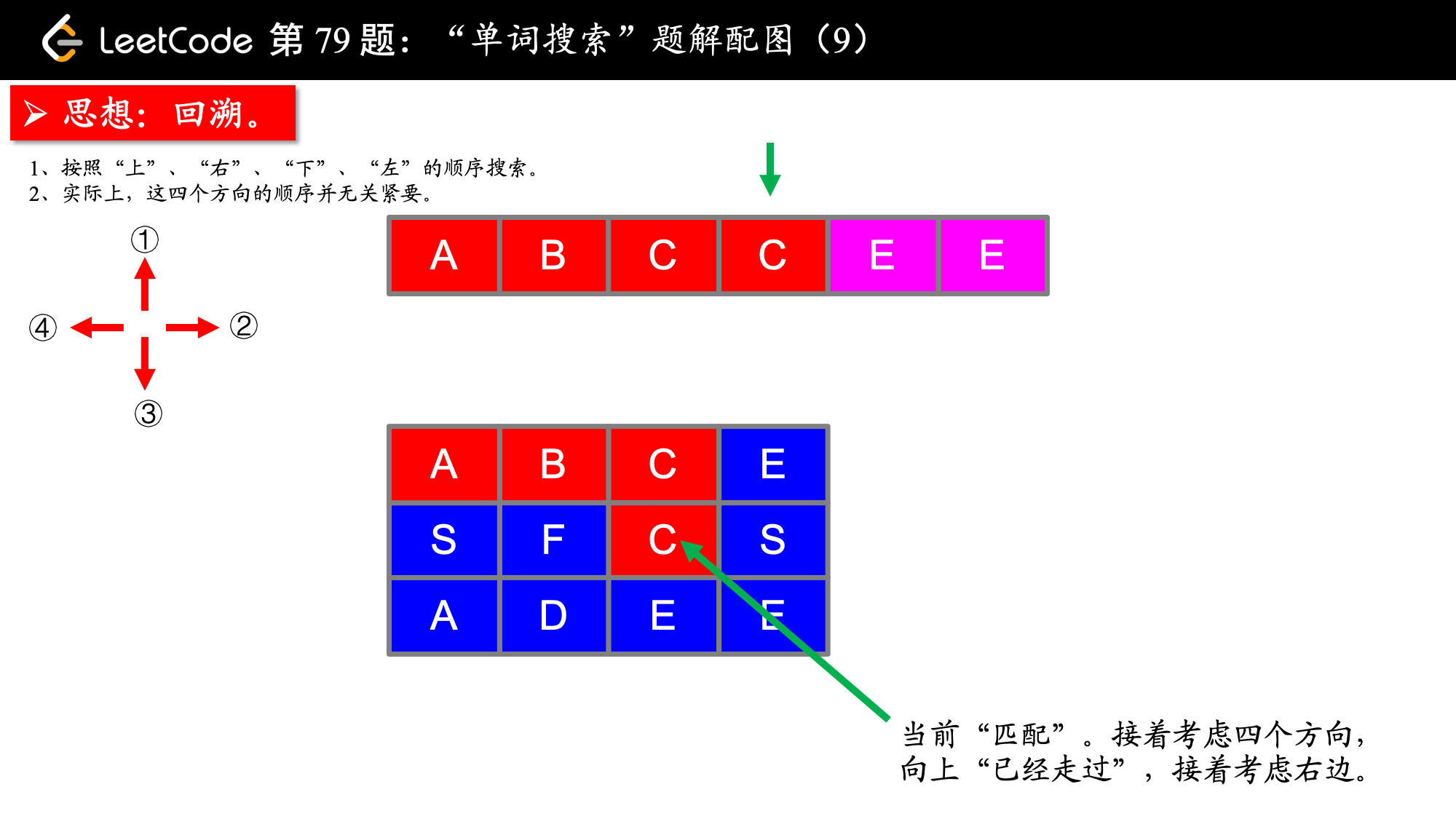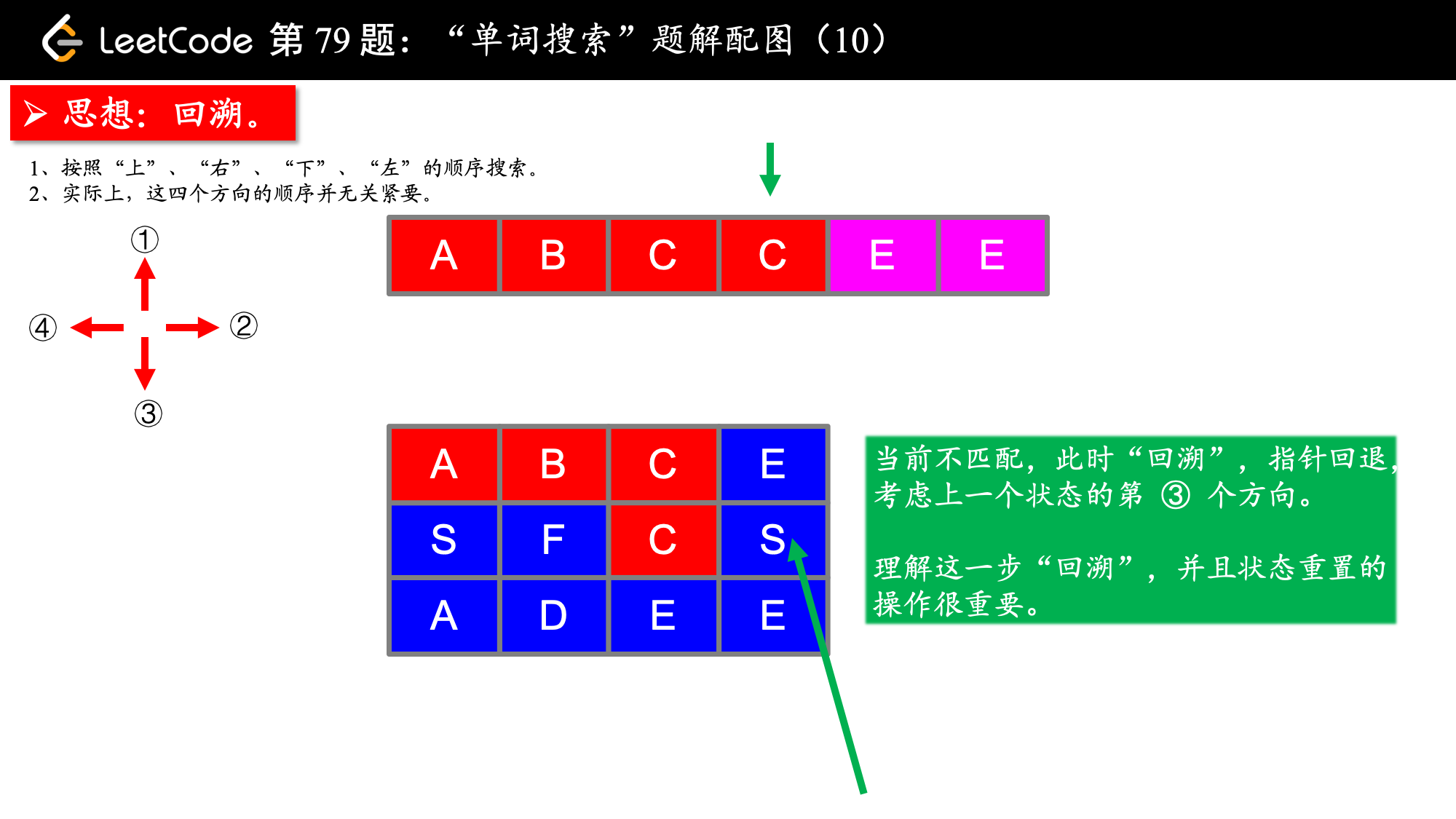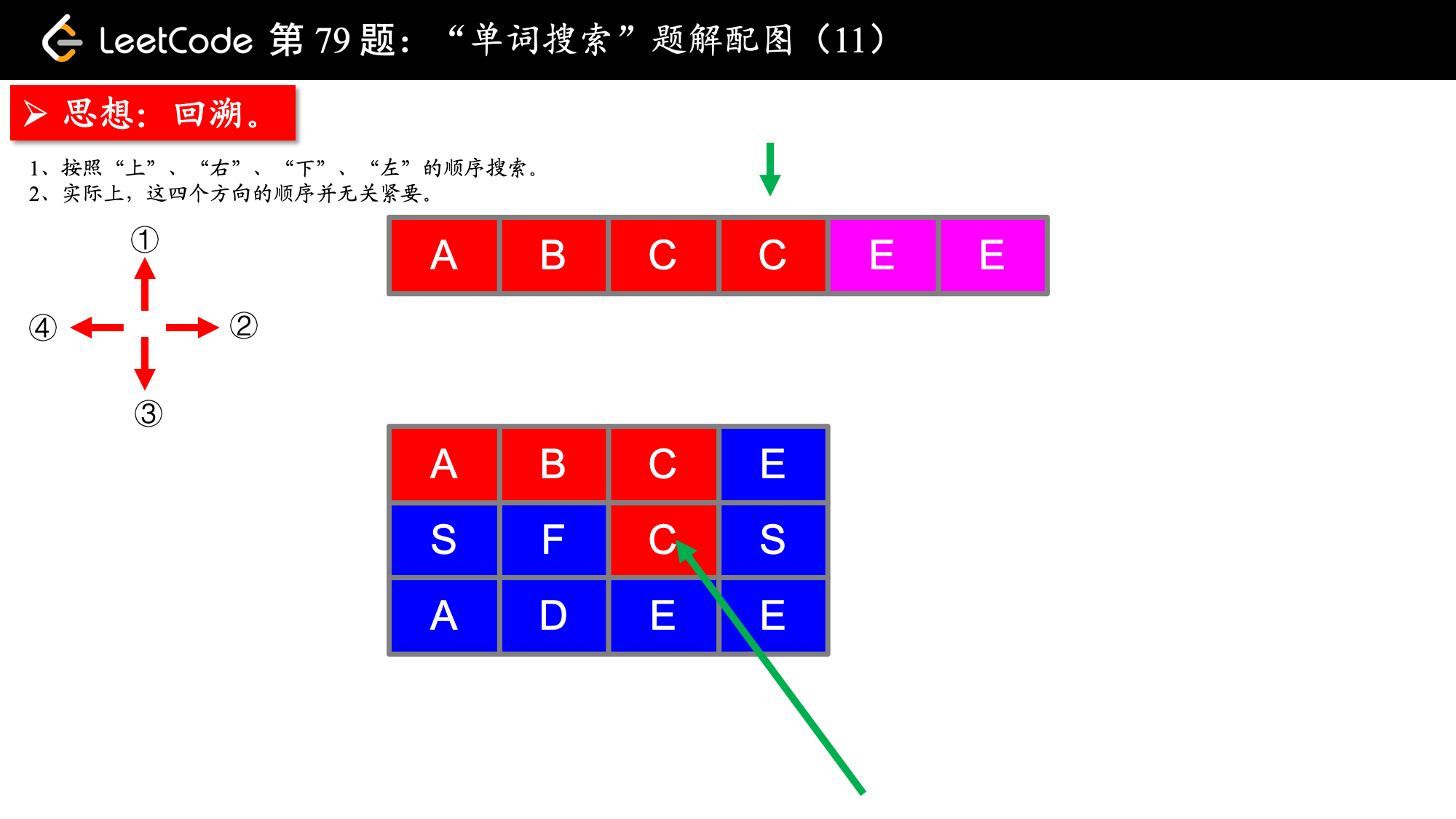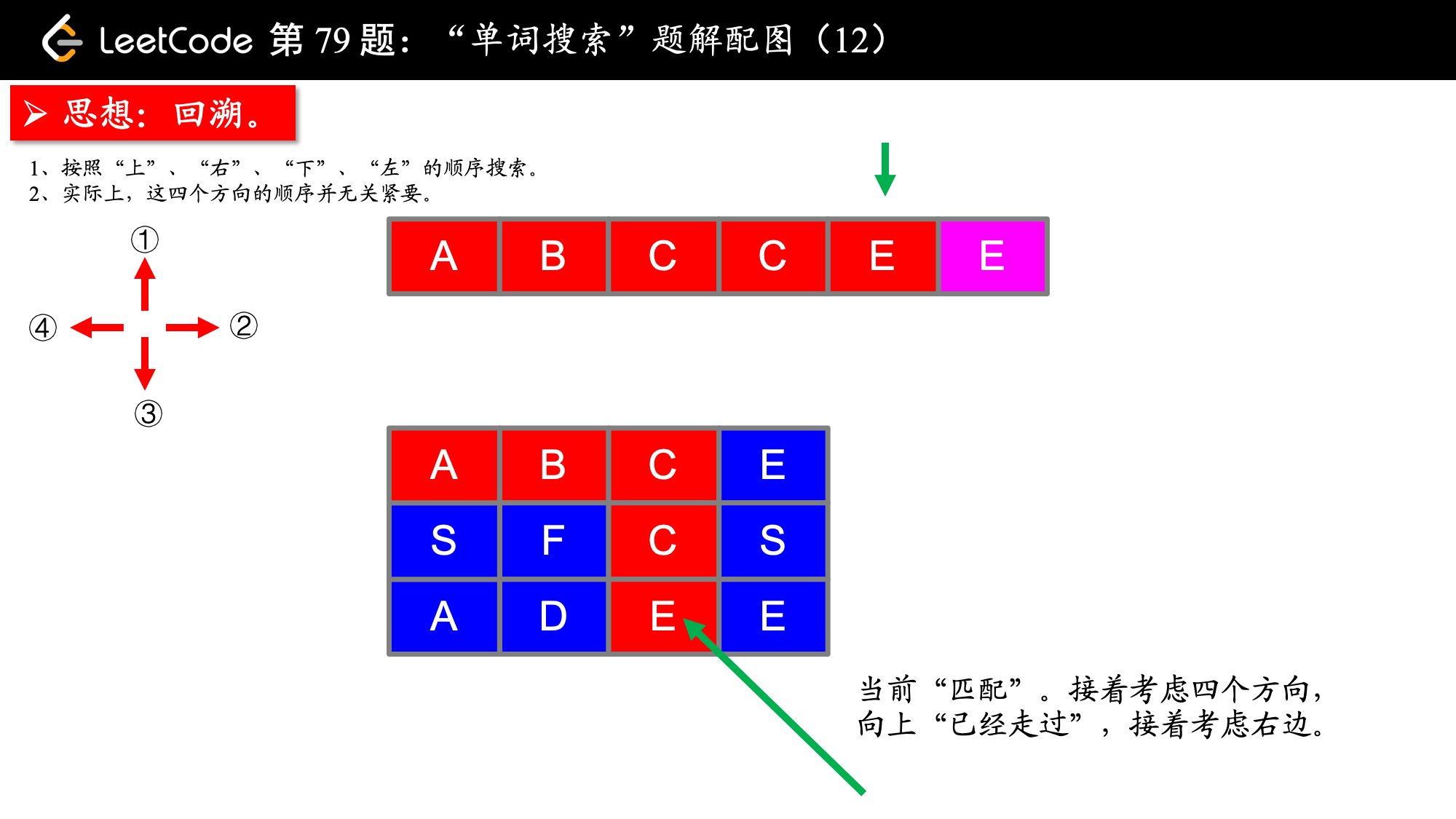79-1.png,79-2.png,79-3.png,79-4.png,79-5.png,79-6.png,79-7.png,79-8.png,79-9.png,79-10.png,79-11.png,79-12.png,79-13.png

参考代码：

Python 代码：

from typing import List


class Solution:
    #         (x-1,y)
    # (x,y-1) (x,y) (x,y+1)
    #         (x+1,y)

    directions = [(0, -1), (-1, 0), (0, 1), (1, 0)]

    def exist(self, board: List[List[str]], word: str) -> bool:
        m = len(board)
        if m == 0:
            return False
        n = len(board[0])

        marked = [[False for _ in range(n)] for _ in range(m)]
        for i in range(m):
            for j in range(n):
                # 对每一个格子都从头开始搜索
                if self.__search_word(board, word, 0, i, j, marked, m, n):
                    return True
        return False

    def __search_word(self, board, word, index,
                      start_x, start_y, marked, m, n):
        # 先写递归终止条件
        if index == len(word) - 1:
            return board[start_x][start_y] == word[index]

        # 中间匹配了，再继续搜索
        if board[start_x][start_y] == word[index]:
            # 先占住这个位置，搜索不成功的话，要释放掉
            marked[start_x][start_y] = True
            for direction in self.directions:
                new_x = start_x + direction[0]
                new_y = start_y + direction[1]
                # 注意：如果这一次 search word 成功的话，就返回
                if 0 <= new_x < m and 0 <= new_y < n and \
                        not marked[new_x][new_y] and \
                        self.__search_word(board, word,
                                           index + 1,
                                           new_x, new_y,
                                           marked, m, n):
                    return True
            marked[start_x][start_y] = False
        return False

Java 代码：

public class Solution {

    private boolean[][] marked;

    //        x-1,y
    // x,y-1  x,y    x,y+1
    //        x+1,y
    private int[][] direction = {{-1, 0}, {0, -1}, {0, 1}, {1, 0}};
    // 盘面上有多少行
    private int m;
    // 盘面上有多少列
    private int n;
    private String word;
    private char[][] board;

    public boolean exist(char[][] board, String word) {
        m = board.length;
        if (m == 0) {
            return false;
        }
        n = board[0].length;
        marked = new boolean[m][n];
        this.word = word;
        this.board = board;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (dfs(i, j, 0)) {
                    return true;
                }
            }
        }
        return false;
    }

    private boolean dfs(int i, int j, int start) {
        if (start == word.length() - 1) {
            return board[i][j] == word.charAt(start);
        }
        if (board[i][j] == word.charAt(start)) {
            marked[i][j] = true;
            for (int k = 0; k < 4; k++) {
                int newX = i + direction[k][0];
                int newY = j + direction[k][1];
                if (inArea(newX, newY) && !marked[newX][newY]) {
                    if (dfs(newX, newY, start + 1)) {
                        return true;
                    }
                }
            }
            marked[i][j] = false;
        }
        return false;
    }

    private boolean inArea(int x, int y) {
        return x >= 0 && x < m && y >= 0 && y < n;
    }

    public static void main(String[] args) {

//        char[][] board =
//                {
//                        {'A', 'B', 'C', 'E'},
//                        {'S', 'F', 'C', 'S'},
//                        {'A', 'D', 'E', 'E'}
//                };
//
//        String word = "ABCCED";


        char[][] board = {{'a', 'b'}};
        String word = "ba";
        Solution solution = new Solution();
        boolean exist = solution.exist(board, word);
        System.out.println(exist);
    }
}

说明：

1、偏移量数组在二维平面内是经常使用的，可以把它的设置当做一个技巧，并且在这个问题中，偏移量数组内的 4 个偏移的顺序无关紧要；

说明：类似使用这个技巧的问题还有：「力扣」第 130 题：被围绕的区域、「力扣」第 200 题：岛屿数量。

2、对于这种搜索算法，我认为理解 DFS 和状态重置并不难，代码编写也相对固定，难在代码的编写和细节的处理，建议多次编写，自己多总结多思考，把自己遇到的坑记下。

我自己在写

for i in range(m):
    for j in range(n):
        # 对每一个格子都从头开始搜索
        if self.__search_word(board, word, 0, i, j, marked, m, n):
            return True

这一段的时候，就傻乎乎地写成了：

# 这一段代码是错误的，不要模仿
for i in range(m):
    for j in range(n):
        # 对每一个格子都从头开始搜索
        return self.__search_word(board, word, 0, i, j, marked, m, n)

这样其实就变成只从坐标 (0,0) 开始搜索，搜索不到返回 False，但题目的意思是：只要你的搜索返回 True 才返回，如果全部的格子都搜索完了以后，都返回 False ，才返回 False。